世界経済のパラメータを探ろう!
各国の経済の推移はその国々の株価指数を比較すると一覧できます。図1は、世界、主要八か所(米国、日本、上海、香港、インド、ドイツ、フランス、英国)の2021年1月4日の株価指数を $1.0$ としたときの、2022年5月10日までの推移です。
図1
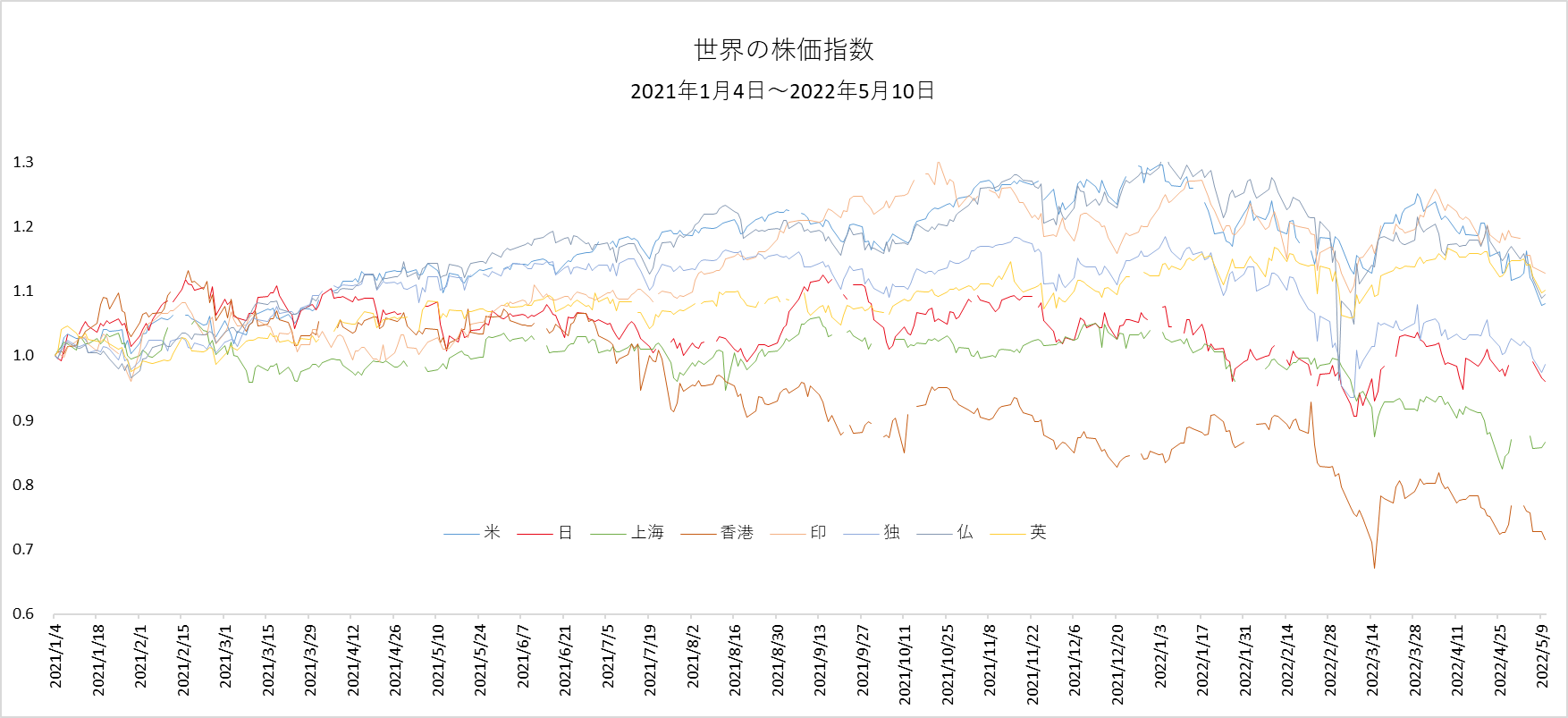
世界、主要八か所の株価指数の推移(2021年1月4日の株価指数 = 1.0 としたとき)2022年5月10日時点での上昇率は、
米国 = 1.081、日本 = 0.960、上海 = 0.867、香港 = 0.715、インド = 1.128、ドイツ = 0.986、フランス = 1.094、英国 = 1.102 、平均 = 0.992
取引所によって営業日数に差異がありますが、上記の間の八か所の平均取引日数は340日でした。もっとも上昇率が高かったのは、インドの 1.128、もっとも低かったのは香港の 0.715 で、その差は 0.413 もあり、かなり明暗が分かれているのがわかります。八か所の平均は、0.992 です。ちなみに、比較基準を五年前の2018年1月5日までさかのぼっても、全体の平均上昇率は、コロナ・ショックの影響もあって、1.072 に留まっています。一日当たりに換算すると、$6.31×10^{-5}$ です。
ところで、株価はランダムに上下運動を繰り返しながら、すこしずつ上昇しようとします。この性質を数式に表すと、
$$\frac{dx}{dt}=rx+v\frac{B(t)}{dt}\tag{1}$$
となります。$x$は株価、$t$ は時間(取引日数)、$r$ は成長率、$v$ はゆらぎ係数(ゆらぎの度合い)、$B(t)$ はランダム(ブラウン)運動です。これは、確率微分方程式と呼ばれ、その解析解(株価 $x$ を時間 $t$ の関数で表したもの)は、
$$f(x)=x_{0}\ e^{(r-\frac{v^2}{2})t+vB(t)}\tag{2}$$
であることがわかっています。$x_{0}$ は初期値($t=0$ のときの $x$ の値)です。この式に含まれるパラメータは $r$ と $v$ のふたつだけですので、基本的にはこのふたつが分かれば式 $(2)$ によって、株価の推移、つまり図1を描くことができます。ちなみに、$B(t)$ はエクセル関数 =RAND() でつくりだすことができます。
上記のとおり、過去五年間の一日あたりの平均上昇率は、$6.31×10^{-5} $ で、これが式 $(2)$ の
$r-\frac{v^2}{2}$ の値ということになります。つまり、
$$r-\frac{v^2}{2}=6.31×10^{-5}\tag{3}$$
で、これが基本成長率です。式 $(3)$ からは、
① 実際の成長率 $r-\frac{v^2}{2}$ はゆらぎ $v$ が加わることで抑制される。
② $\frac{v^2}{2}$ が $r$ を超えると、成長率がマイナスになる。
③ $r$ か $v$、どちらか一方の係数が決まればもう一方も同時に決まる。
ことがわかります。百聞は一見にしかずですので、実際にやってみましょう。③より、ゆらぎ係数 $v$ を選んだら、成長率 $r$ が自動的に決まりますので、$v$ を $0.01$ → $0.015$ → $0.03$ と徐々に大きくしながら、それぞれ三十回試行します。
このとき、初期値 $x_{0}$ が $1.0$、基本成長率が $6.31×10^{-5}$ ですので、基本成長線(以下 µ)は、
$$f(x)=e^{6.31×10^{-5}t}\tag{4}$$
です。下図では赤線で示しました。
図2
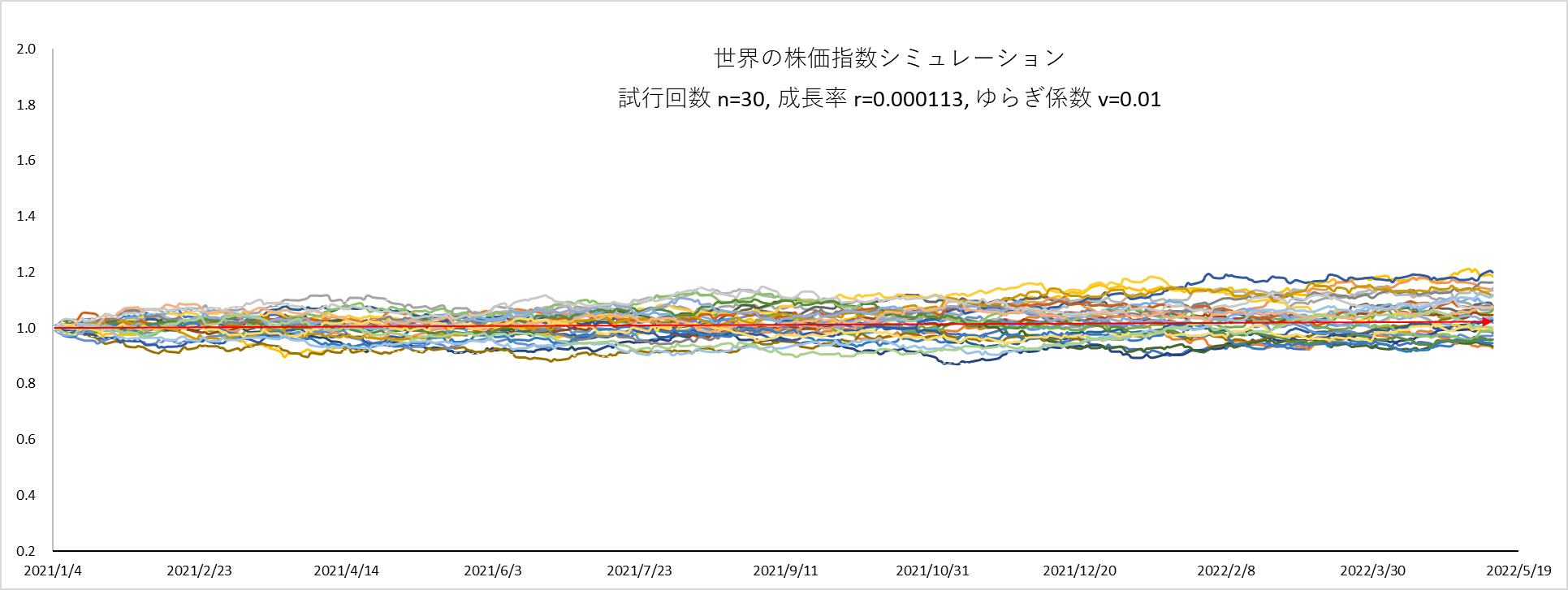
$v=0.01, r=1.13×10^{-4}$
30本のうち、21本がプラス成長、9本がマイナス成長
t=351 (2022年5月10日)時点の振れ幅は、0.93~1.20(µ=1.02)
図3

$v=0.015, r=1.76×10^{-4}$
30本のうち、19本がプラス成長、11本がマイナス成長
t=351 (2022年5月10日)時点の振れ幅は、0.73~1.43(µ=1.02)
図4

$v=0.03, r=5.13×10^{-4}$
30本のうち、15本がプラス成長、15本がマイナス成長
t=351 (2022年5月10日)時点の振れ幅は、0.51~2.22(µ=1.02)
ちなみに、縦軸を対数にすると、µ(赤線)はゆらぎの中央に移動します。図5は図4の縦軸を対数に変換したものです。
図5

縦軸を対数にとると µ(赤線)は中央に移動する
ゆらぎ係数 $v$ が大きくなるにつれて株価の振れ幅が大きくなり、二倍くらいに成長するものも出てくる一方で、マイナス成長になる確率が高まることがわかります。ブレが大きいと、「良いことよりも、悪いことの方が多い」ということですから、実に興味深い結果です。詳細にご興味のあるかたは、2021年5月31日付けのブログ「数理経営のすすめ その2「ゆらぎ」 ブレない経営の数理的意味」をご覧ください。
図2、図3、図4で、実際の振れ幅である図1に最も近いのが図3です。その図3をよく観察すると、試行した三十本はそれぞれ独立に(ばらばらに)動いていることがわかります。一方、図1の八本の実績はばらばらではなく、一体感があり、一定のリズムが感じられます(註)。そのリズムを矢印で示したのが図5です。
図5
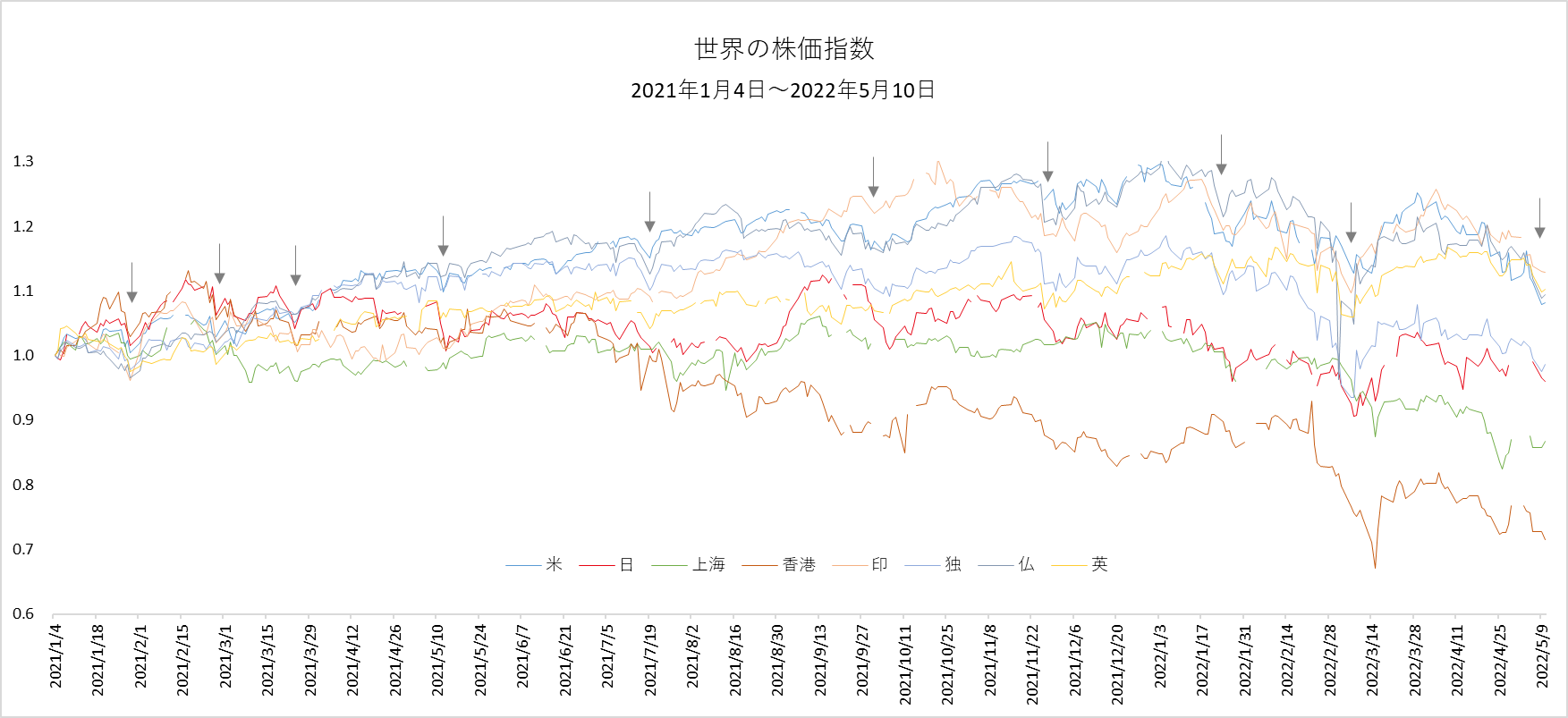
世界の株価指数には周期的なリズムがある!
では、この周期的なリズムを数値シミュレーションにどう反映したらいいでしょうか。ゆらぎ係数の $v$ を定数ではなく時間の関数にしてサインカーブ で揺らしてみましょう。もともと $v=0.015$ でしたから、
$$v=0.015+ksin(wt)\tag{4}$$
と表現できます。サインカーブは振幅 $k$ と角振動数 $w$ を変化させることで波の形を自由に変えることができます。図6は、$k=0.012$、$w=0.087$ として、30回試行した結果です。
図6
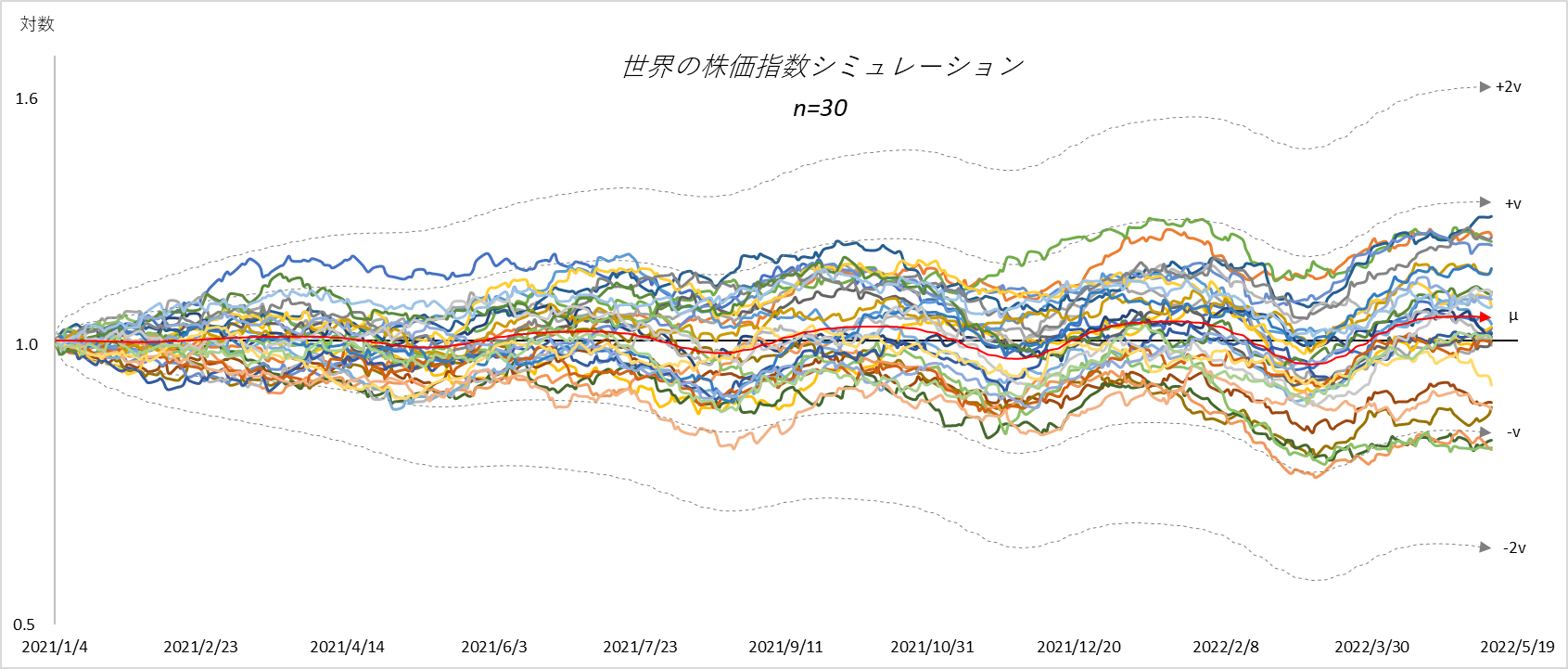
µ中心線 $e^{(r-\frac{v^{2}}{2})t}$ +v線 $e^{(r-\frac{v^{2}}{2})t+v\sqrt{t}}$ -v線 $e^{(r-\frac{v^{2}}{2})t-v\sqrt{t}}$ +2v線 $e^{(r-\frac{v^{2}}{2})t+2v\sqrt{t}}$ -2v線 $e^{(r-\frac{v^{2}}{2})t-2v\sqrt{t}}$
$r=1.76×10^{-4}, v=0.015+0.012*sin(0.087t)$
最後に、実績の中に上記の µ 線と ±v 線を描き加えてみましょう。横軸は2022年の末まで延長しました。
図7
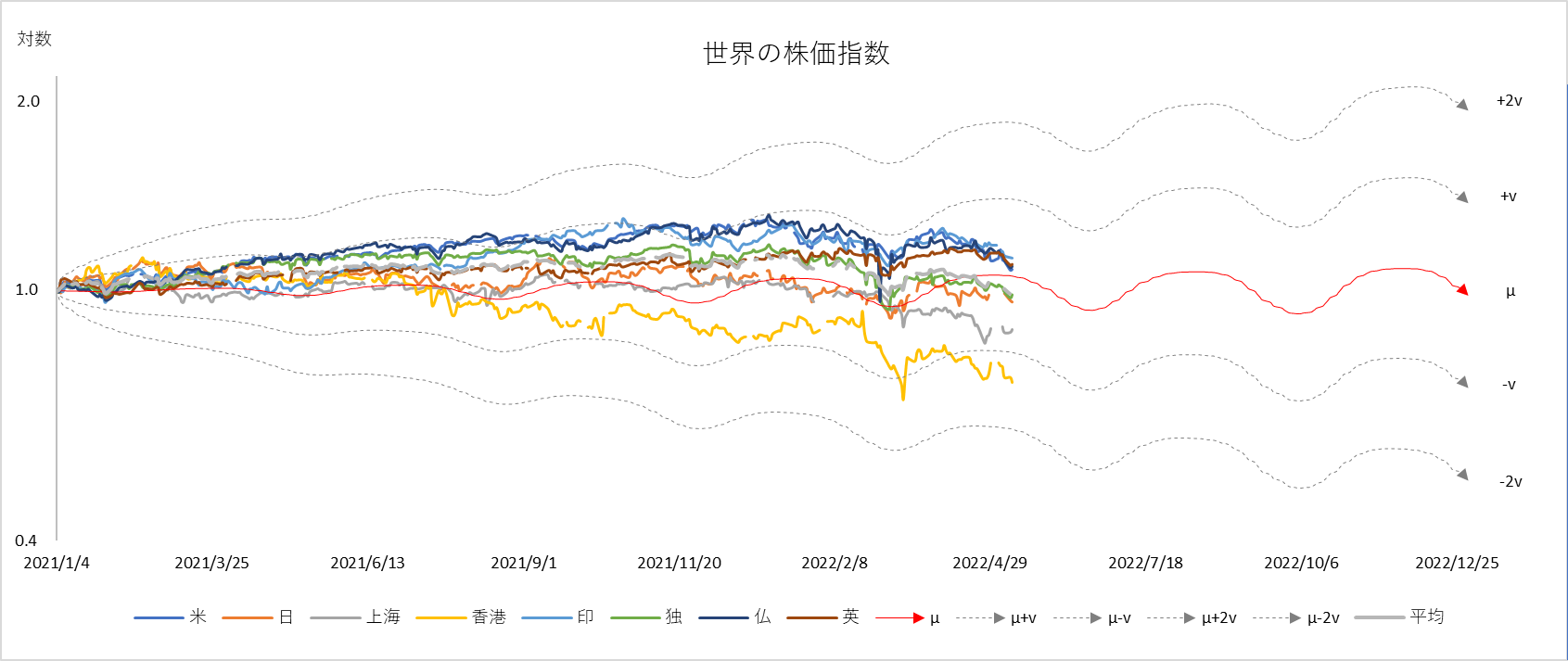
$r=1.76×10^{-4}, v=0.015+0.012*sin(0.087t)$
2021年1月4日を $1.0$ としたときの2022年12月末の振れ幅予測:$+v=1.38$ $-v=0.70$ $+2v=1.94$ $-2v=0.50$
ふたつのパラメータ $r$ と $v$ がわかったことで近未来予測ができるようになりました。2022年末に実績と照合してみましょう。
(註)下の表が2021年1月から2022年5月までの八か所の株価指数の相関係数です。米国、インド、ドイツ、フランス、英国のグループと、日本、上海、香港のグループにかなり強い正の相関関係があります。

おわり
記事一覧へ戻る