2021年5月6日付のブログ、数理経営のすすめ – その1「成長」でいろいろな成長曲線を描く方法をご紹介しました。左側が経営者の基本行動パターン、右側がその成長曲線の特長です。
$\frac{dx}{dt}=α\tag{1}$ → 右肩上がりの直線(定額成長するモデル)
$\frac{dx}{dt}=rx\tag{2}$ → 下に凸の曲線(指数関数増加する定率成長モデル)
$\frac{dx}{dt}=rx(1-\frac{x}{K})\tag{3}$ → S字曲線(上限Kに収束するモデル)
$\frac{dx}{dt}=at+b\tag{4}$ → 下に凸の曲線(成長が時間経過とともに漸減するモデル)
さて、これまで経営者の「基本行動パターン」を記号 $\frac{dx}{dt}$ と称して使ってきましてが、これは実は、数学的には「$x$ の 時間微分」を意味します。会社は経営者の基本行動パターンの積み重ねによって成長しますが、それは数学でいう微小時間 $dt$ における変化量 $dx$ の積み重ね、つまり「積分」と同じだと捉えているわけです。積分すると$x$ を時間 $t$ の関数として表すことができます。つまり、将来を予測することができるということです。
では、上記の四つの微分方程式をそれぞれ積分して $x$ を時間 $t$ の関数で表してみましょう。$x_{0}$ は初期値です。
$\frac{dx}{dt}=a$ → $x_{t}=at+x_{0}$
$\frac{dx}{dt}=rx$ → $x_{t}=x_{0}e^{rt}$
$\frac{dx}{dt}=rx(1-\frac{x}{K})$ → $x_{t}=\frac{K}{1+(\frac{K}{x_{0}}-1)e^{-rt}}$
$\frac{dx}{dt}=at+b$ → $x_{t}=\frac{a}{2}t^2+bt+x_{0}$
積分で得られた右側の式で計算した値を、時間 $t$を横軸に、 $x$ を縦軸にとってグラフにすると、成長曲線が現われます。とてもシンプルな一方で、係数を選択した時点で自ずと将来が決まるという「決定論的」な面があります。実際のビジネスは、景気や気候変動、経営者の迷い、交代等、いろいろな不確定要素の影響を受けます。そしてその結果、成長が「ゆらぎ」ます。
本日はその「ゆらぎ」を数理モデルに取り入れることを考えます。
「ゆらぎ」の数理的表現
エクセルには乱数を発生させる機能があります。任意のセルに =RAND() と打ち込みファンクションキーの F9 を繰り返し押してみてください。0 ~ 1 の間の値をランダムに返してきます。次に、=NORMINV(RAND(),0,0.6) と打ち込んで F9 キーを繰り返し押してください。今度は平均(µ)0、標準偏差(σ)0.6 の値をランダムに返してきます。
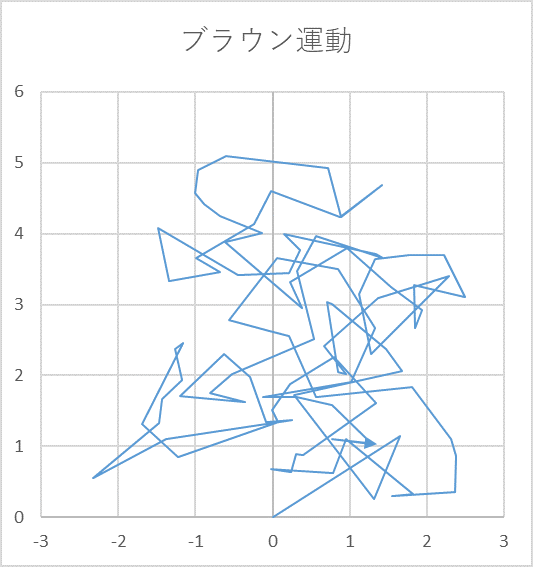
この方法で 100 個の数字を二列にならべ、その二列のデータを縦軸と横軸に選んだ散布図を作成します。そうすると図1のような軌跡が現われます。F9 キーを繰り返し押すと、次々と形が変わってなかなか飽きません。これが「ブラウン運動」です。
図0
(x,y)=(0,0) からはじまるブラウン運動、平均 µ= 0、標準偏差 σ=0.6、n=100 ステップ
以後、このブラウン (Brown) 運動を「ゆらぎ」と呼び、 その微小時間における変化を $\frac{dB}{dt}$ とします。ゆらぎの度合いを $v$ (volatility)とすると、付け加えるべき「ゆらぎ項」 は $vx\frac{dB}{dt}$ となります。では、上にあげた四つのモデルにこの「ゆらぎ項」がどのような影響を与えるかをみていきます。
ゆらぎ項を加えた定額成長:
$$\frac{dx}{dt}=α+vx\frac{dB}{dt}\tag{1}$$
図1
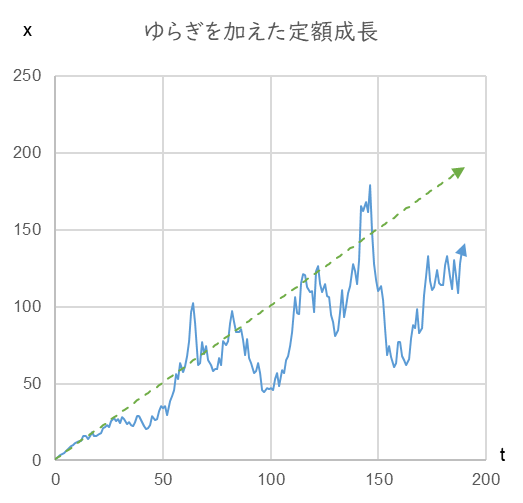
α=1.0, v=0.2, dB/dt=NORMINV(RAND(),0,0.6)、x0=1.0
緑の破線はゆらぎのない成長、青の実線がゆらいだときの成長の一例
ゆらぎ項を加えた定率成長:
$$\frac{dx}{dt}=rx+vx\frac{dB}{dt}\tag{2}$$
図2
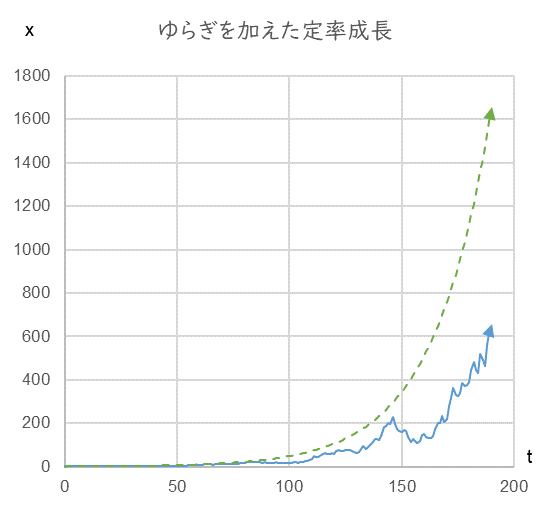
r=0.04, v=0.2, dB/dt=NORMINV(RAND(),0,0.6)、x0=1.0
緑の破線はゆらぎのない成長、青の実線がゆらいだときの成長の一例
ゆらぎ項を加えた上限(S字)成長:
$$\frac{dx}{dt}=rx(1-\frac{x}{K})+vx\frac{dB}{dt}\tag{3}$$
図3
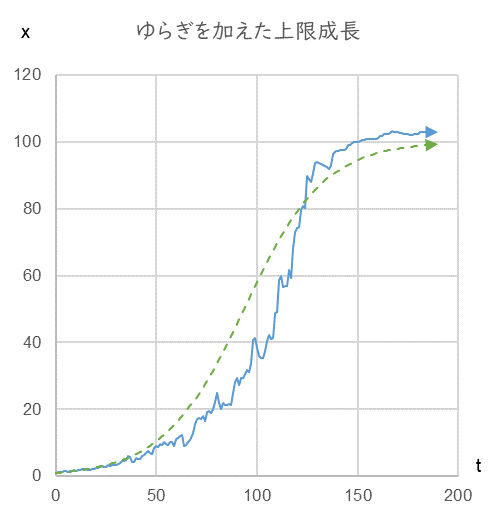
r=0.04, K=100, v=0.2, dB/dt=NORMINV(RAND(),0,0.6)、x0=1.0
緑の破線はゆらぎのない成長、青の実線がゆらいだときの成長の一例
ゆらぎ項を加えた成長が時間経過とともに漸減するモデル:
$$\frac{dx}{dt}=at+b+vx\frac{dB}{dt}\tag{4}$$
図4
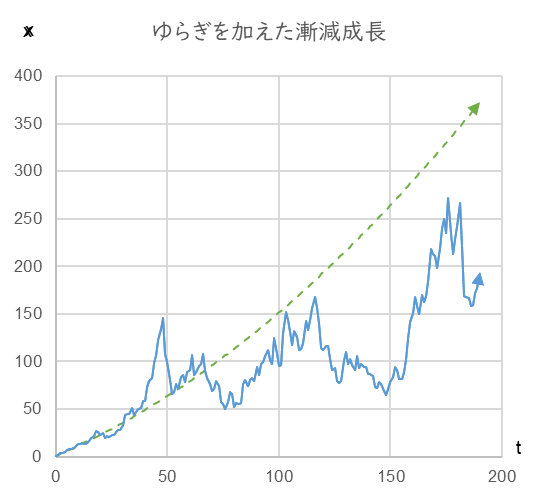
a=0.01, b=1.0, v=0.2, dB/dt=NORMINV(RAND(),0,0.6)、x0=1.0
緑の破線はゆらぎのない成長、青の実線がゆらいだときの成長の一例
さて、ここで式 (2) に注目します。
$$\frac{dx}{dt}=rx+vx\frac{dB}{dt}\tag{2}$$
まずは、この式から図2を描く方法ですが、いたってシンプルです。図5のように初期値に変化量である $\frac{dB}{dt}$ を次々と積み上げていくだけです。値がマイナスのときはその分下げます。
図5

ここで、任意の時間 $t$ における $x$ の値を一気に計算したいときは、冒頭の説明のとおり、式 (2) を積分します。その過程は省略しますが、積分結果は以下のとおりです。
$$x_{t}=x_{0}e^{(r-\frac{v^2σ^2}{2})t+vB}\tag{5}$$
ここで、$r$ は成長係数、$v$ はゆらぎ係数、$σ$はブラウン運動の標準偏差、$B$ はブラウン運動(=NORMINV(RAND(),µ,σ)です。「ゆらぎ」があるため未来は確定的ではなく確率的に決まります。
具体的に計算してみましょう。係数と初期値は図2と同じ、$v$ を 0.1、0,2、0.3 にそれぞれ設定して計算した結果が図6-1~3 です。グラフ中の「中心線」とは式 (5) から、ゆらぎを取り払った式 (6) のことです。
$$x_{t}=x_{0}e^{(r-\frac{v^2σ^2}{2})t}\tag{6}$$
中心線の上下で彗星のしっぽのように右上に流れているグレイの破線は、ゆらぎ係数の $v$ を ±1倍、±2倍と変化させたときに $x$ が確率的に分布する範囲を示しています。数式は以下の通りです。
$$x_{t}=x_{0}e^{(r-\frac{v^2σ^2}{2})t±□v\sqrt{t}}\tag{7}$$
縦軸に注意してください。サンプル・パスの分布を見やすくするために対数にしてあります。
図6-1
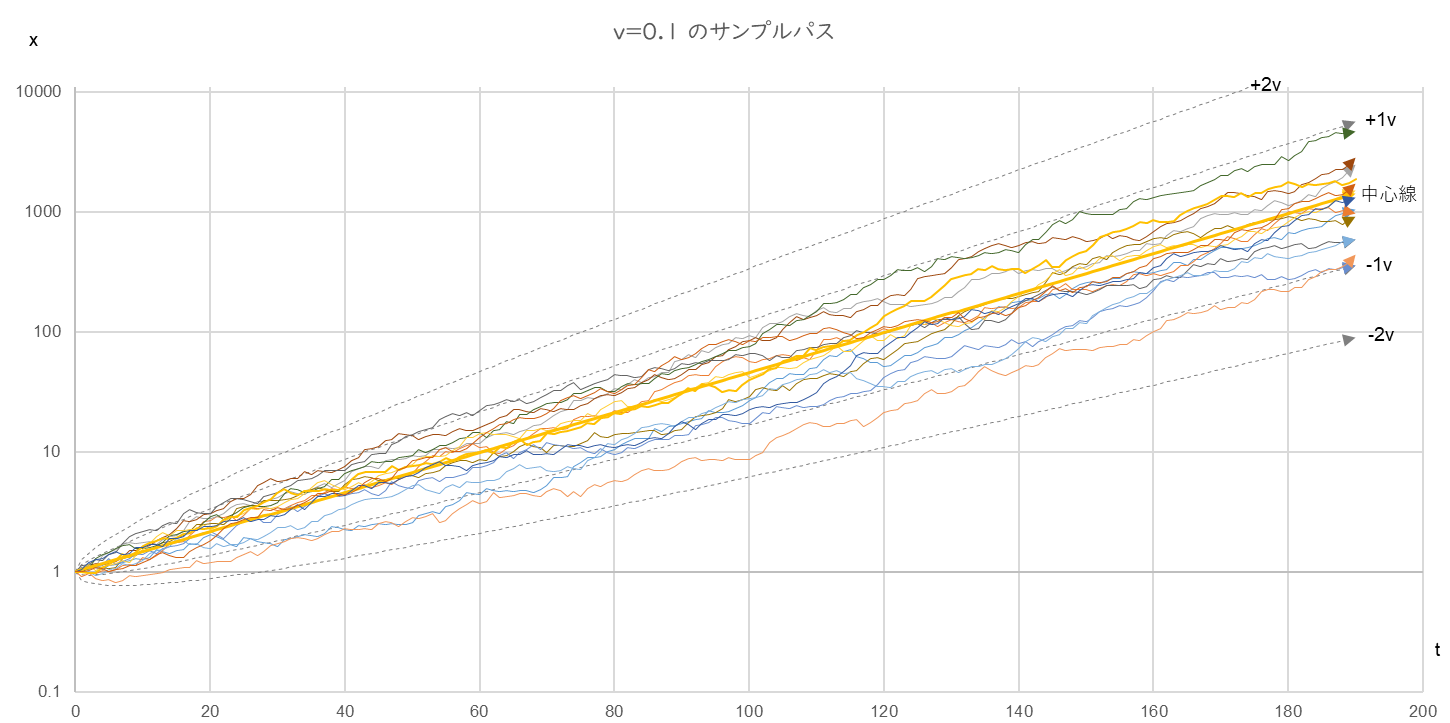
r=0.04, v=0.1, µ=0.0, σ=0.6, x0=1.0, n=14
図6-2
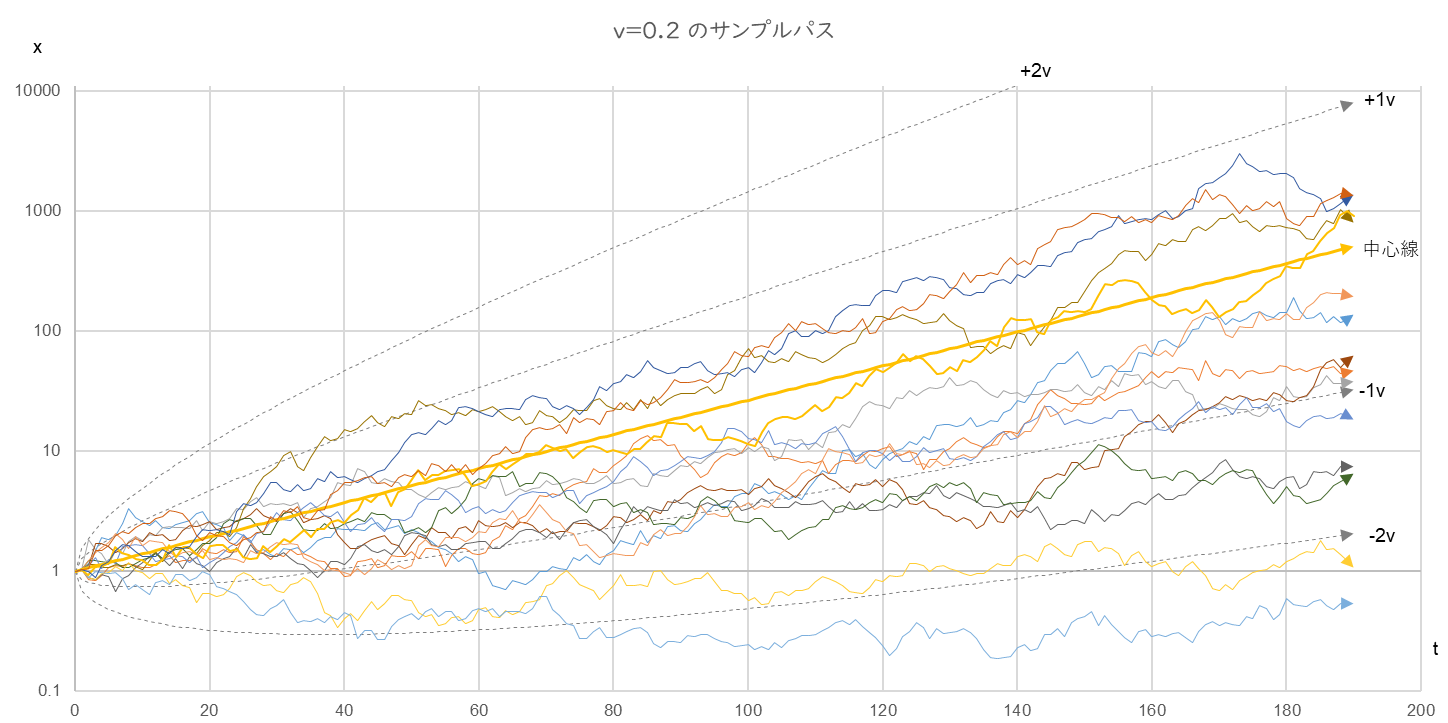
r=0.04, v=0.2, µ=0.0, σ=0.6, x0=1.0, n=14
図6-3
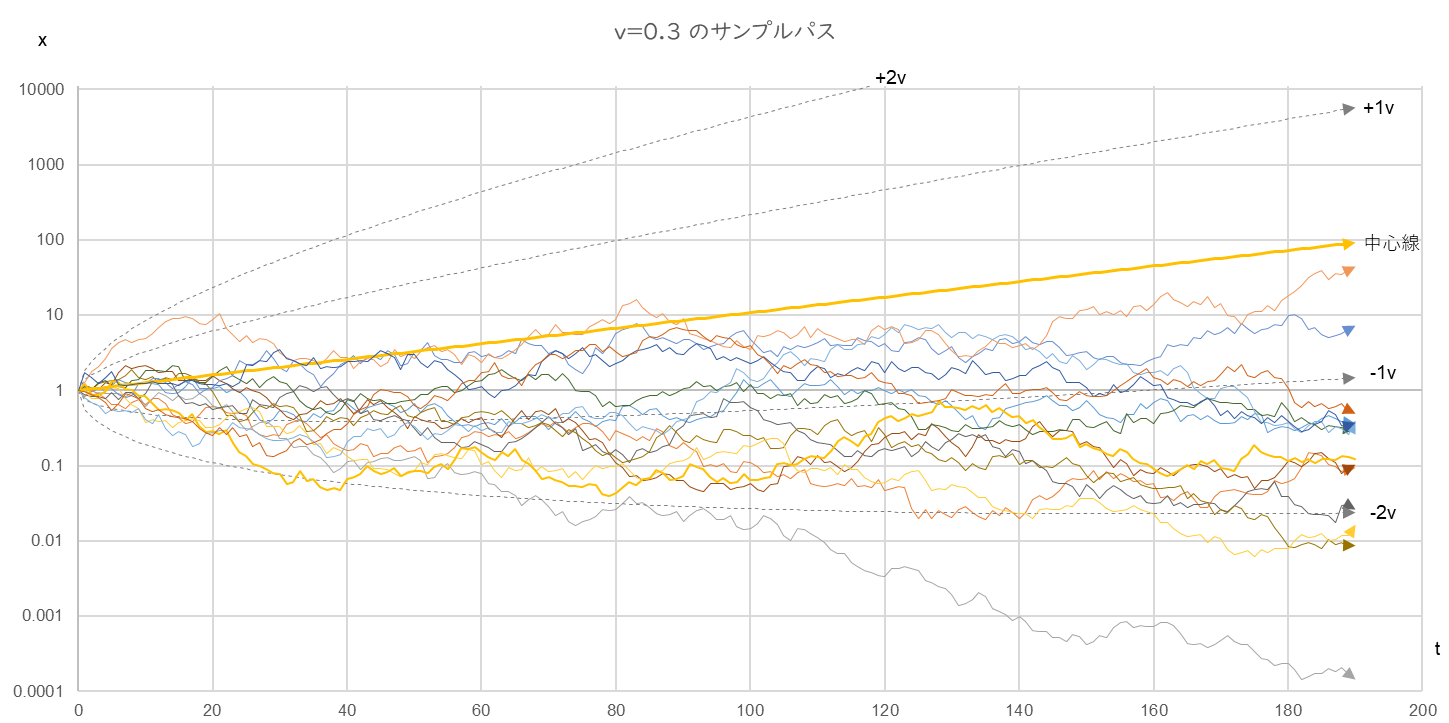
r=0.04, v=0.3, µ=0.0, σ=0.6, x0=1.0, n=14
図6-1~3をじっくり見くらべると、ゆらぎ係数 $v$ が大きくなると全体の右上がりの傾きが緩やかになることが分ります。たとえば t=100 のサンプル・パスは、v=0.1 のときはおおよそ 10~100の間に分布していますが、v=0.2 のときは 0.1~70の間、v=0.3 になると 0.01~5 の間へと下降しています。また、v=0.2 までは、t=190 で中心線の上にあるサンプル・パスは5~6本ありますが、v=0.3 になるとすべて中心線の下にあることもわかります。
これは非常に重要なことを示唆しています。経営者が迷えば迷うほど、会社の成長力が削がれてしまうであろうことは「経験的」、「感覚的」には理解できますが、ここでやった計算はその「数学的証明」といえます。私はこのことに気が付いたときとても感動しました。
式 (5) は会社の成長は基本的に 成長係数の $r$ によってもたらされることを示していますが、その同じ式の中に $r$ の力を削ぐ ゆらぎ係数 $v$ がこっそりと潜んでいたのです!裏を返せば、$v$ の値を小さく抑え込むことがすなわち、より大きな成長をもたらす首尾一貫した、ブレのない経営だということになります。
「数理経営のすすめ – その3」 へつづく
< 追記:2021年5月31日 >
図1~4と図6の詳細は ゆらぎ – Excel を開いてみてください。
図6の「中心線」と「確率分布域(彗星のしっぽ」は株価の動きで実際に観察することができます。以下は米国の代表的な株価指数である S&P500 の動きです。新型コロナ・ウィルス・ショックからの回復がきれいに +2v 曲線に沿っているのがわかります。詳細は S&P500 – Excel をご覧ください。
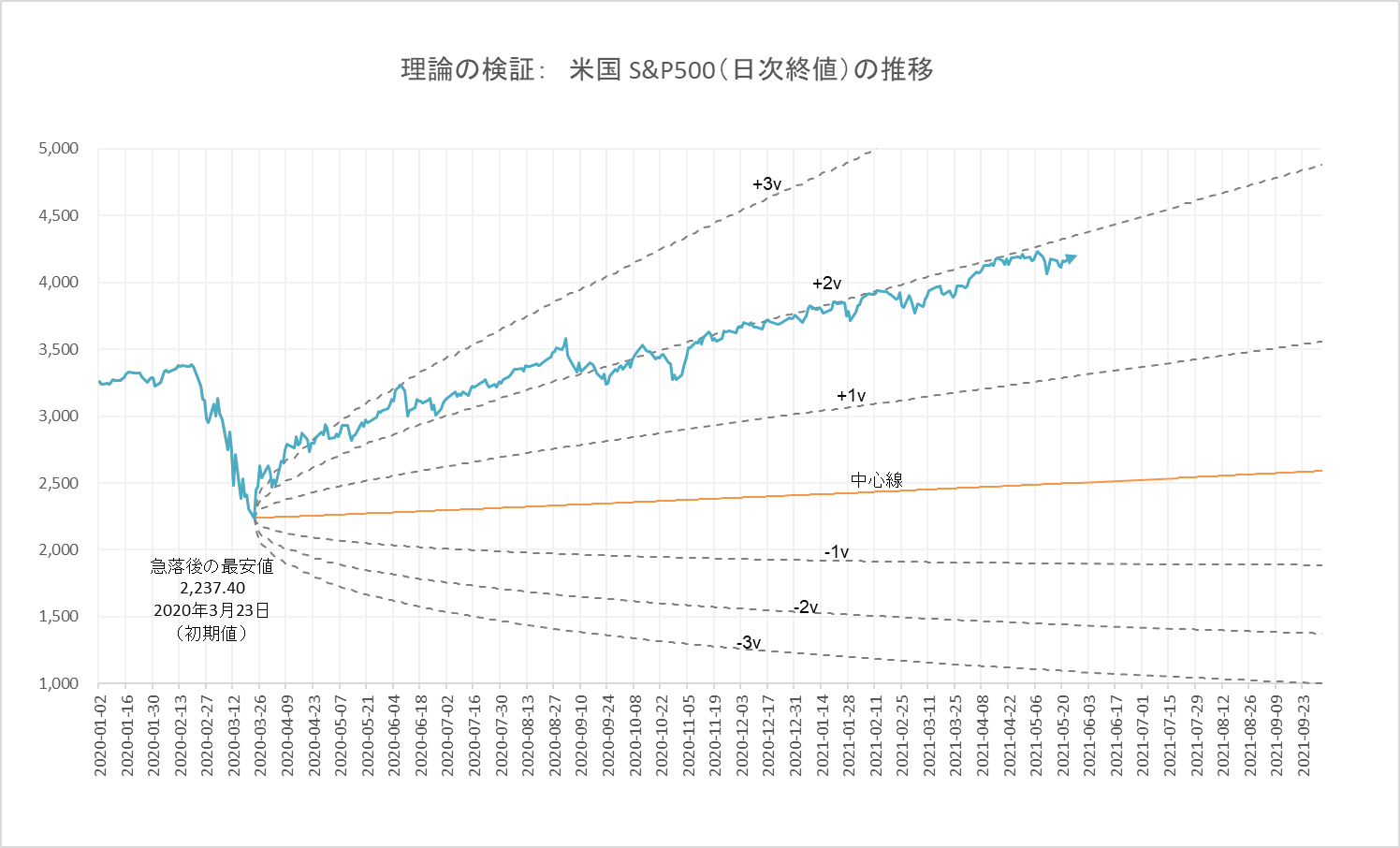
米国S&P500の日次終値の推移
数式 (6)と(7)に、x0=2,237.40、r=0.00042、v=0.016、σ=0.6 を代入して計算した中心線(オレンジの実線)と確率分布曲線(グレイの破線)
以上
記事一覧へ戻る