「コロナ禍の売上急落の不安を払拭する超簡単な数式」を 2021年9月3日付のブログでご紹介しました。その数式とは以下です。

$$x_{t}=αx_{t-1}+µ+ε_{t}\tag{1}$$

x_t は時間 t における売上、 x_t-1 はそのひとつ前の売上です。α は売上係数、µ は定数。ε_t は誤差項です。この単純な数式が、コロナ禍で落ち込んだ売上が必ずまた元の状態にもどることを教えてくれました。このとき、コロナ禍は ε_t に大きなマイナスの値を与えて表現しましたが、今回はその逆、プラスの場合を検証してみましょう。

まずは、刺激が通常の範囲で入る状態を確認しましょう。

図１

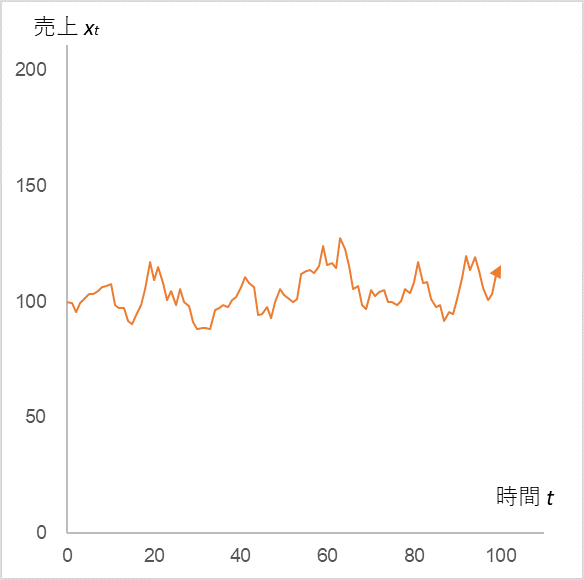
式（1）に、α=0.9、µ=10、平均=0、標準偏差=5 の正規分布に従う ε_t を代入して計算したときの売上 x_t （初期値=100）の時系列変化

 

初期値の 100 を中心に上下運動が続きます。ここで、t=10～13 の ε_t を +50、 +40、 +30、 +20 に置き換えます。

図２

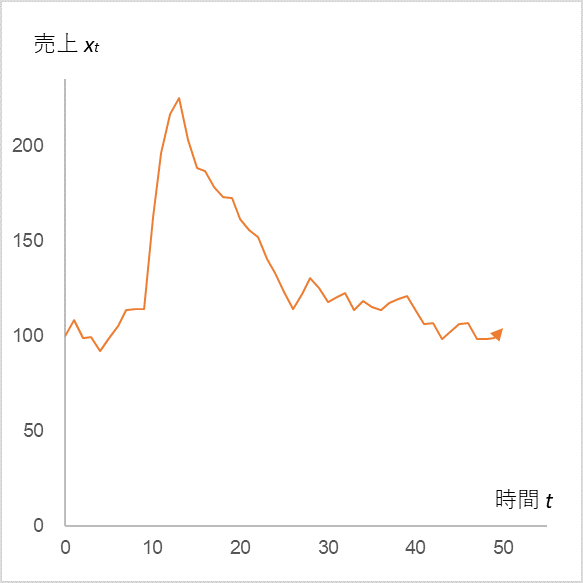
式（1）に、α=0.9、µ=10、平均=0、標準偏差=5 の ε_t を代入して計算したときの売上 x_t （初期値=100）の時系列変化

（但し、ε_t は、t=10 のとき +50、t=11 のとき+ 40、t=12 のとき +30、t=13 のとき +20）

 

t=10～13 の売上はプラスの刺激を受けて大きく跳ね上がりますが、またすぐにもとのギザギザ状態に戻ってしまいます。広告宣伝活動によって売上が急伸したとしても、活動をやめてしまうとすぐにまたもとの売上に戻ってしまうのはこれが理由です。では、広告宣伝活動を継続する場合はどうでしょうか。t=14 以降の ε_t の平均を 0 から 10 へ上げてみましょう。

図３

図2において、t=14 以降の ε_t の平均を 0 から 10（標準偏差は 5のまま）に上げたときの売上 x_t の時系列変化 

 

確かに、売上は上がったままの状態で維持されています。「継続は力なり」です。テレビで同じメーカーのコマーシャルを何度もみる理由、展示会に行くと出展している会社がいつも同じである理由、もこれでわかります。

刺激が入っても、またもとのレベルにもどってしまう理由は、式（1）を以下のように展開するとわかります。

$$x_{0}$$

$$x_{1}=αx_{0}+µ+ε_{1}$$

$$x_{2}=αx_{1}+µ+ε_{2}=α(αx_{0}+µ+ε_{1})+µ+ε_{2}=α^2x_{0}+µ(1+α)+(αε_{1}+ε_{2})$$

$$x_{3}=αx_{2}+µ+ε_{3}=α(α^2x_{0}+αµ+αε_{1}+µ+ε_{2})+µε_{3}=α^3x_{0}+µ(1+α+α^2)+(α^2ε_{1}+αε_{2}+ε_{3})$$

・

・

・

$$x_{t}=αx_{t-1}+µ+ε_{t}=α^tx_{0}+µ(1+α+α^2+α^3+ ・・・+α^t)+(α^{t-1}ε_{1}+α^{t-2}ε_{2}+α^{t-3}ε_{3}+・・・+ε_{t})\tag{2}$$

式（2）はみっつの項から構成されています。

第一項の $α^tx_{0}$ は、α<1 のときゼロに近づきます。初期値 x₀ はこの第一項にしか現れず、それが t の進行によって消えてしまいますので、x_t の収束値は初期値 x₀ の値によらずに決まります。 

第二項の $µ(1+α+α^2+α^3+ ・・・+α^t)$ は α<1 のときある一定の値に収束します。たとえば、µ=10、α=0.9 のときは 100 に、µ=10、α=0.5 のときは 20 に収束します。

第三項の $α^{t-1}ε_{1}+α^{t-2}ε_{2}+α^{t-3}ε_{3}+・・・+ε_{t}$ は誤差項です。誤差は正規分布すると仮定しており、係数 α がかかっているだけで正規分布することに変わりはありません。α の値によってギザギザ度（標準偏差）が変化します。

 

時系列分析シリーズは次の「経営者が目線を上げる、数理的意味」（2021年9月13日付ブログ）が最後です。

 

＜参考文献＞

沖本竜義、AR過程、経済・ファイナンスデータの計量時系列分析、朝倉書店、2021

 

記事一覧へ戻る