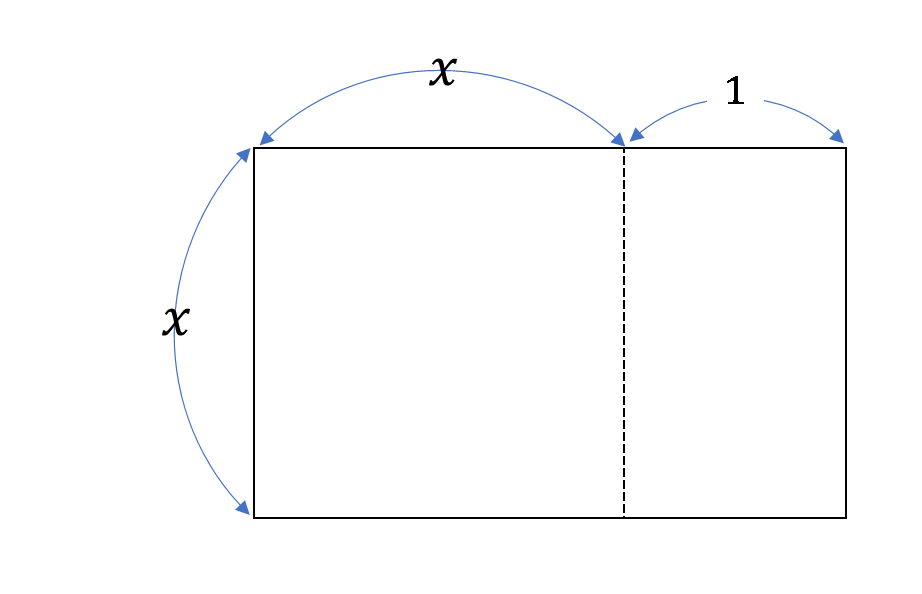
黄金数とは、下の長方形において、以下の式が成り立つ $x$ の値のことをいいます。
$$\frac{x+1}{x}=x\tag{1}$$
図1
式 $(1)$ を変形すると、
$$x^2-x-1=0\tag{2}$$
これは $x$ の二次方程式ですから、解の公式を使うと、$x$ はすぐに求めることができ、
$$x=\frac{1+\sqrt{5}}{2}≒1.618\tag{3}$$
です。この一見中途半端な値がいかに神秘的かという話を、2022年6月22日付のブログ「黄金比が神秘的な理由」で紹介しました。本日は、図1を長方形ではなく、円にしてみましょう。
図2

黄金数は長方形と同じ要領で、式 $(4)$ を満たす $x$ です。
$$\frac{360}{x}=\frac{x}{360-x}\tag{4}$$
つまり、
$$x^2+360x-360^2=0\tag{5}$$
二次方程式の解の公式より、
$$x=222.5\tag{6}$$
が求まり、
$$360-x=137.5\tag{7}$$
となります。$222.5$ 度を $137.5$ 度で割ると、$1.618$ ですので、黄金数になっています。
ちなみに、丸いピザを分割したときにできる、一片のピザの角度は、
二分割のとき $180$ 度
三分割のとき $120$ 度
四分割のとき $90$ 度
五分割のとき $72$ 度
六分割のとき $60$ 度
七分割のとき $51$ 度
八分割のとき $45$ 度
九分割のとき $30$ 度
となりますが、$137.5$ 度や $222.5$ といった中途半端な角度はどこにも出てきません。ピザを $137.5$ 度に切ったところで、大き過ぎて食べにくいだけで、なんのご利益もなさそうです。では、ピザではなく、葉っぱだとしたらどうでしょうか?植物を真上からみたときの葉の配置に注目してみましょう。
まず、 $x=120$ のときは、
図3
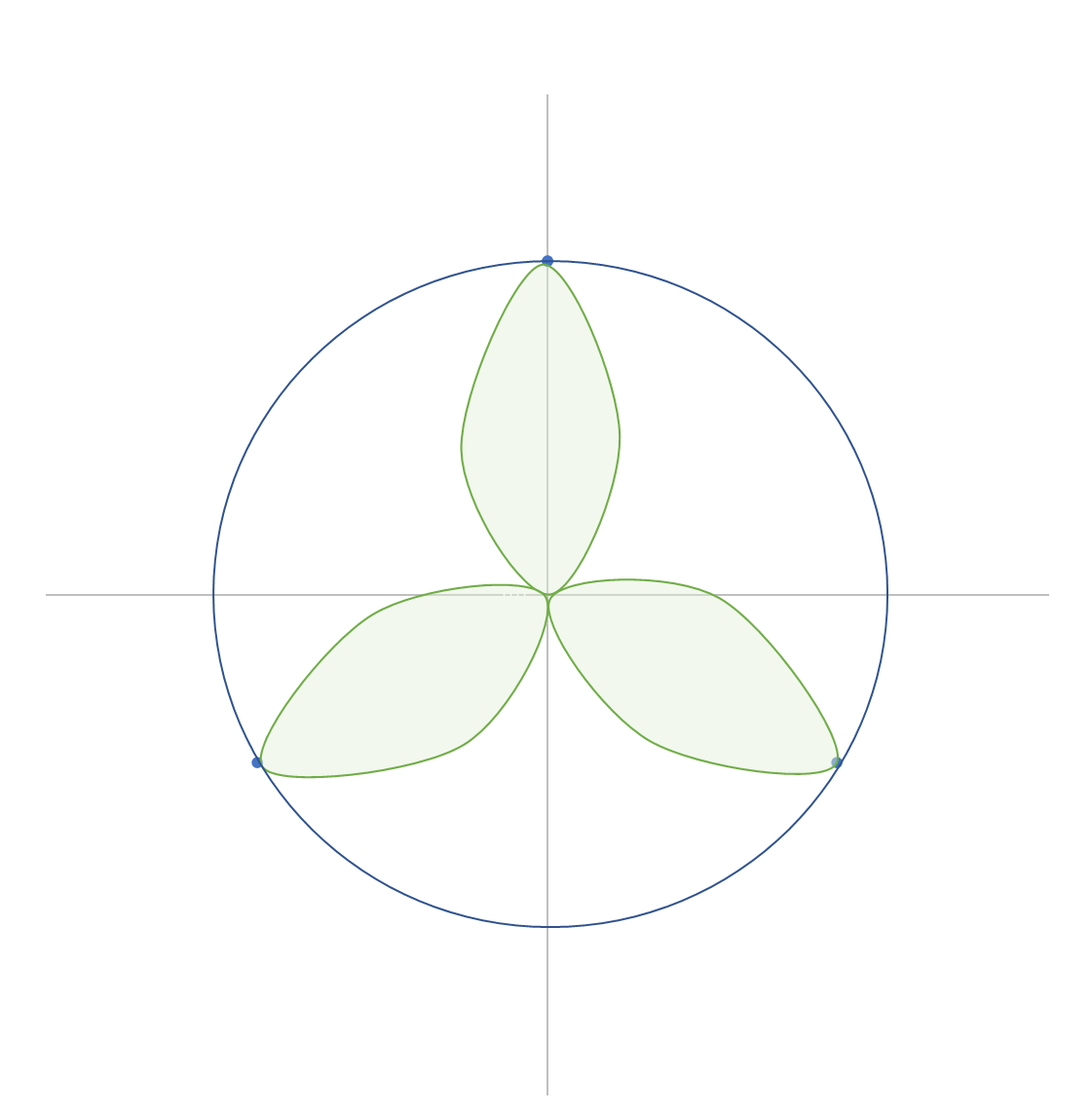
となり、一回転すると四枚目の葉は一枚目の葉に重なってしまいます。円の中で葉っぱが占める面積はかなり少なく、光合成ができるスペースがまだたくさん残っています。
では、$x=90$ のときはどうでしょう?
図4
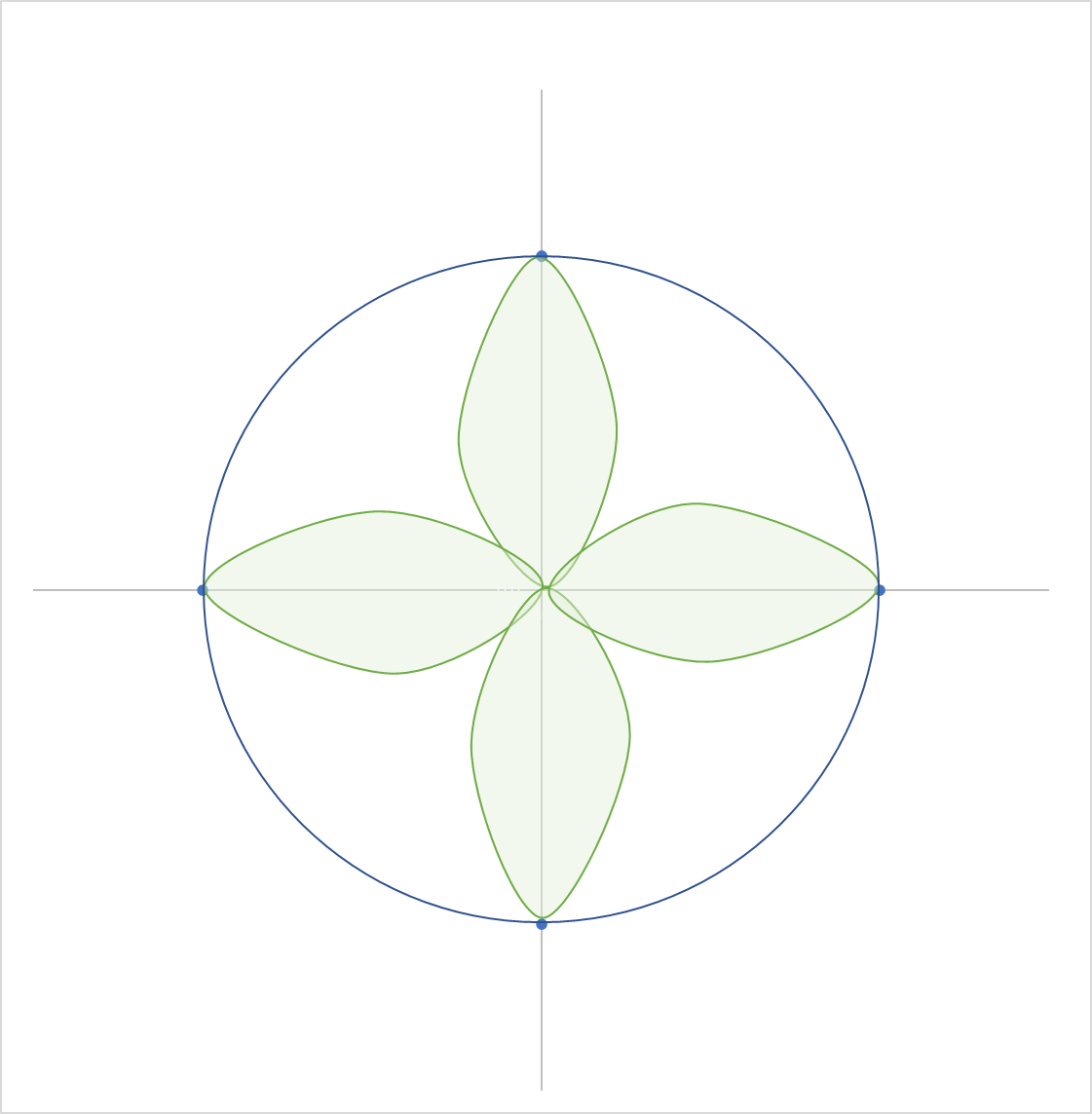
まだまだ利用できるスペースがあります。
$x=45$ になると、
図5
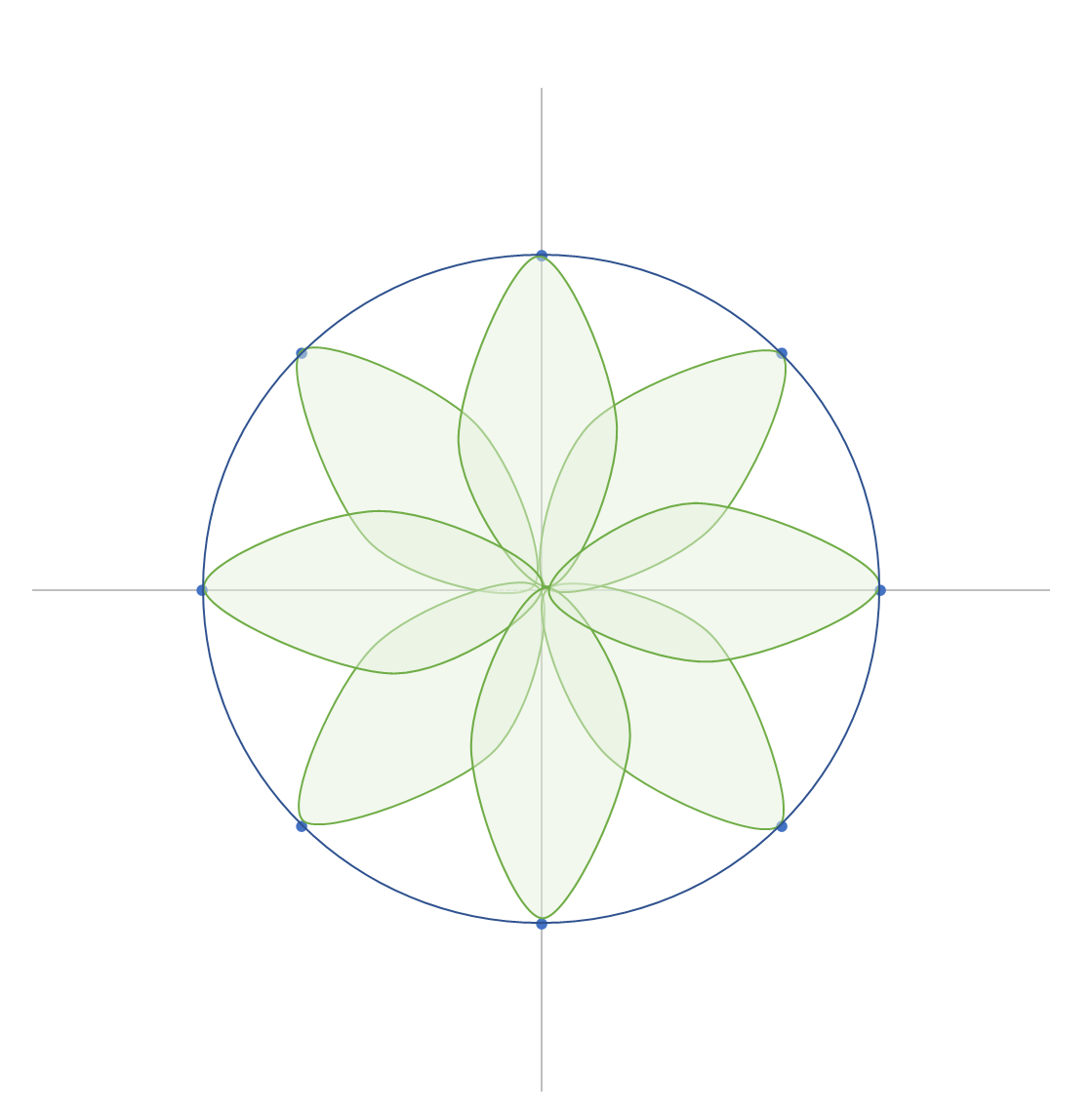
さらにスペースを有効活用できているのがわかりますが、9枚目の葉は1枚目に重なってしまいますので、これ以上余白を埋めることはできません。
そこで、黄金角 $x=222.5$ の登場です。
図6

ここでは22枚まで図示しましたが、このまま、葉の枚数を増やしても重なることなく、デッドスペースは完全に埋め尽くされます。つまり、黄金角は植物が最も太陽光を無駄なく使える角度といえそうです。
では、実際の植物を少し観察してみましょう。以下の写真は私が街で見つけた植物を真上から撮影したものです。
図7




どれも葉と葉が重ならないように努力しているのがわかります。ざっとみたところ、90度回転と120度回転が多いようですが、自然界は三次元で光を受けますし、太陽光の差し込む角度も時々刻々と変わりますので、上下の葉が多少重なっていても十分な光を受けることができそうです。
おわり
記事一覧へ戻る