黄金比とは、以下の図形の縦横の比のことをいいます。
$$1.618:1=(1.618+1):1.618\tag{1}$$
図1
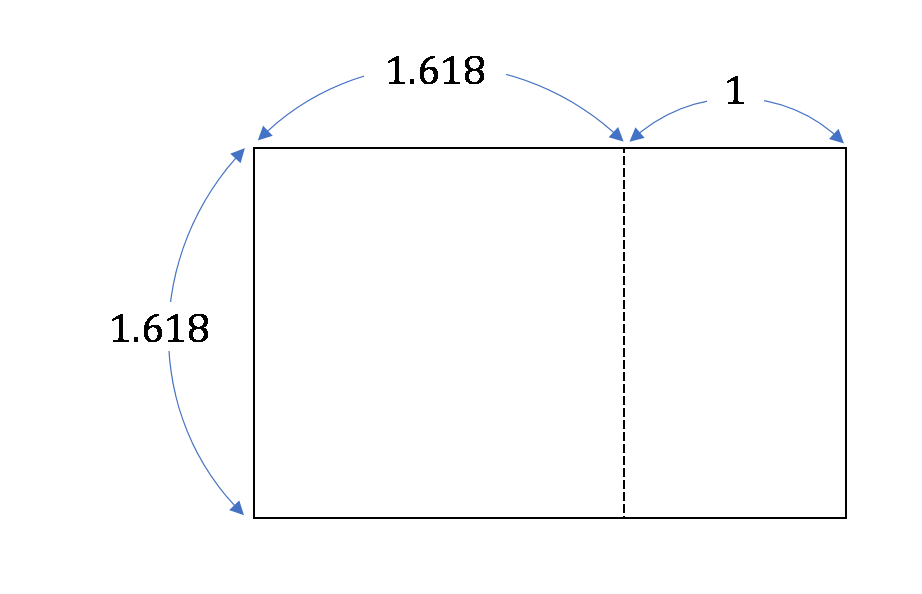
$1.618$ とは、また中途半端な数字ですが、「長方形の長辺の $2.618$ を短辺の $1.618$ で割ると、短辺と同じ $1.618$ になっている」、というのがミソです。この長方形は我々人類が、世の東西を問わず、もっとも美しいと感じる比率のようです。「黄金比の実例」でググってみると、建造物では、パルテノン神殿、サグラダ・ファミリア、金閣寺、凱旋門、ピラミッド、自然界では、貝の形、花や葉の形、芸術では、ミロのヴィーナスやモナ・リザ、身近なところでは、名刺、キャッシュカードやクレジットカード、トランプ、パソコンのワイドモニターなどが、ほぼ黄金比になっているようです。確かにいわれてみると、心地よい安定感がありますし、とにかくバランスがいいような気がします。
では、そもそも $1.618$ という数字はどこから出てきたのでしょうか?もし、それが未知の数 $x$ であったとすると、図1は、図2のように描けます。
図2
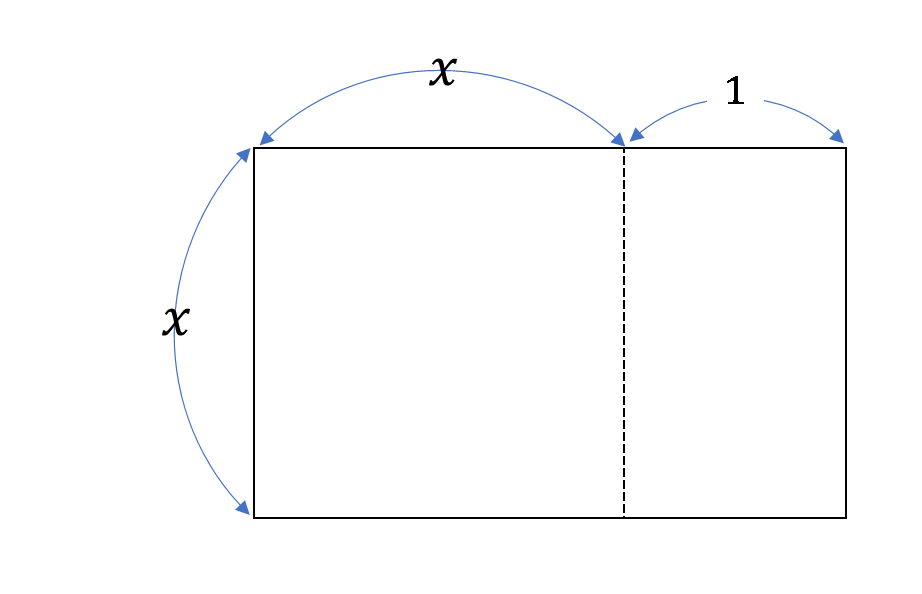
長方形の長辺の長さ $x+1$ を、短辺の長さ $x$ で割ると、また短辺の長さ $x$ になるわけですから、それを数式で表すと、
$$\frac{x+1}{x}=x\tag{2}$$
となります。変形すると、
$$x^2-x-1=0\tag{3}$$
です。これは $x$ の二次方程式ですから、解の公式を使うと、$x$ はすぐに求めることができます。つまり、
$$x=\frac{1+\sqrt{5}}{2}≒1.618\tag{4}$$
です。確かに、$1.618$ という数字が出てきました。でもその数字自体、見た目がきれいでもありませんし、「黄金の輝き」があるとも思えません。
ではここで、式 $(3)$ を以下のように変形してみます。
$$x^2=x+1\tag{5}$$
両辺を $x$ で割ります。
$$x=1+\frac{1}{x}\tag{6}$$
右辺の $x$ に、式 $(6)$ を代入します。
$$x=1+\frac{1}{1+\frac{1}{x}}\tag{7}$$
これを、繰り返すと、
$$x=1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+…}}}}}\tag{8}$$
のように永遠に $1$ だけしか出て来ない、美しい分数(連分数)になります!
では、実際に式 $(6)~(8)$ を使って計算をしてみます。$x=0.5$、$x=1$、$x=2$ の三パターンでやってみましょう(小数点第五位を四捨五入)。
表1
| n | x=0.5 | x=1.0 | x=2.0 |
| 1 | 3.0000 | 0.5000 | 1.5000 |
| 2 | 1.3333 | 1.6667 | 1.4000 |
| 3 | 1.7500 | 1.6000 | 1.7143 |
| 4 | 1.5714 | 1.6250 | 1.5833 |
| 5 | 1.6364 | 1.6154 | 1.6316 |
| 6 | 1.8111 | 1.6190 | 1.6129 |
| 7 | 1.6207 | 1.6176 | 1.6200 |
| 8 | 1.6170 | 1.6182 | 1.6173 |
| 9 | 1.6184 | 1.6180 | 1.6183 |
表1をグラフにしたものが図3です。$x$ の初期値に寄らず、振動しながら $1.618$ に収束している様子が分かります。
図3
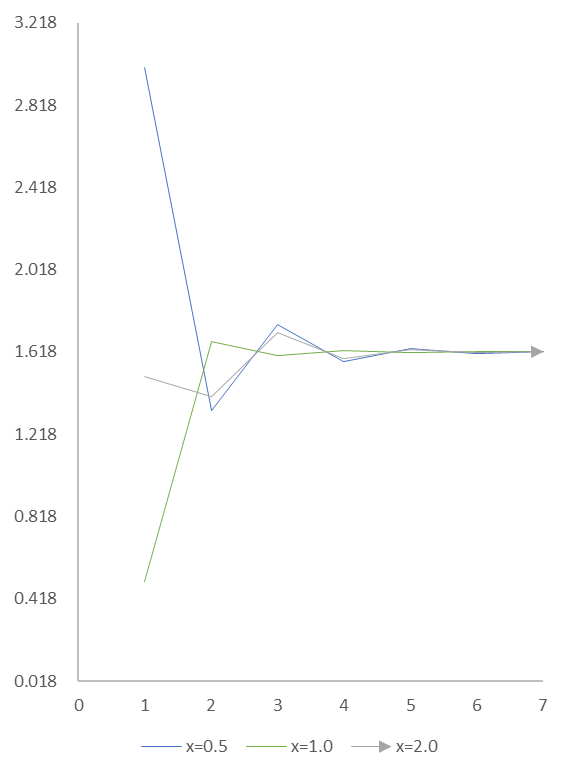
$x$の初期値によらず 1.618 へ収束する連分数
黄金の輝きを放っているのは、黄金比そのものというよりは、黄金比を導く連分数の方ではないでしょうか。
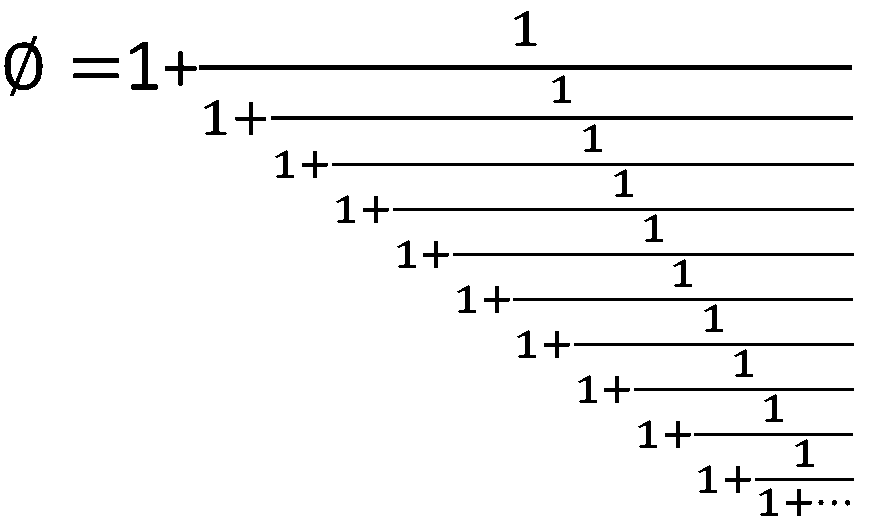
以下は、数学大図鑑(Newton Press, 2022, p54)の抜粋です。
黄金数は、数学的にも美しい!
黄金数($Φ$)を分数であらわすと、数式の中にでてくるのは1だけである。単純で非常に美しい黄金数の連分数は、実に神秘的だ。
おわり
記事一覧へ戻る