売上が何らかの理由で一時的に急落すると、誰しも心理的な圧迫感を感じるものです。しかも、それがいつ回復するのか、もしかするとこのまま回復しないのか、など、どうしても否定的な思案をめぐらせてしまいがちです。特に、今もコロナの影響で売上が落ち込んでいる業界、店舗は、いつこの苦境から抜け出せるのかと不安な日々が続きます。

本日は、「非常に単純な数式がその不安を払拭する」という話をします。まずはともあれ、その数式をみましょう。

$$x_{t}=αx_{t-1}+µ+ε_{t}\tag{1}$$

ここでは、x_t を時間 t における売上とします。よって、 x_t-1 はそのひとつ前の売上という意味です。α は売上係数、µ は定数。ε_t は売上の自然な上下運動（ランダム項）です。ひとつ前の売上に一定の係数をかけて、定数とランダム項を加えたら現在の売上になる、というだけのことす。これがどうして落ち込んだ売上からの不安を払拭してくれるのでしょうか？何はともあれ、計算してみましょう。

仮に、t=0 のときの売上 x₀ を 100 、売上係数 α を 0.9、定数 µ を 10 とします。ランダム項の ε_t は平均 0、標準偏差 5 の正規分布に従うとします。そうすると、売上 x_t の時系列変化は図１のようになります。

図１

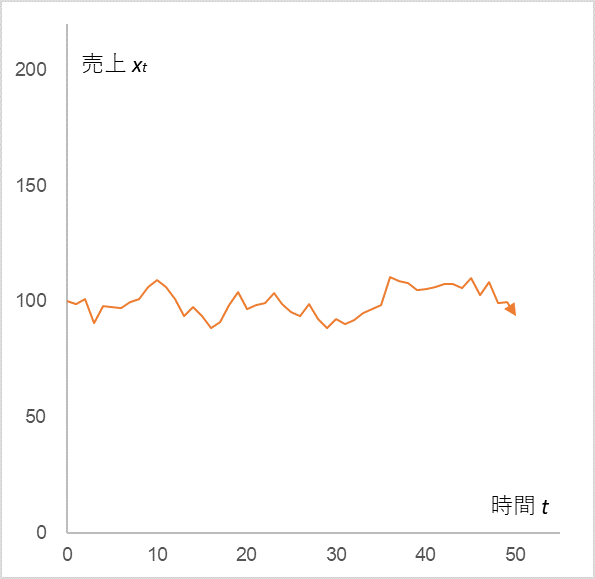
初期売上 x₀=100, 売上係数 α=0.9, 定数 µ=10, ランダム項 ε_t=（平均 0、標準偏差5）の確率正規分布

 

通常の売上 100 を中心にして上下運動しています。これが、コロナがないときの売上推移です。ここに、t=10～13 でコロナがやってきたとします。それを計算に反映するには、ランダム項 ε₁₀ ～ ε₁₃ の値を強制的に大きなマイナスにします。さて、売上はどう変化するでしょう？図２をご覧ください。

図２

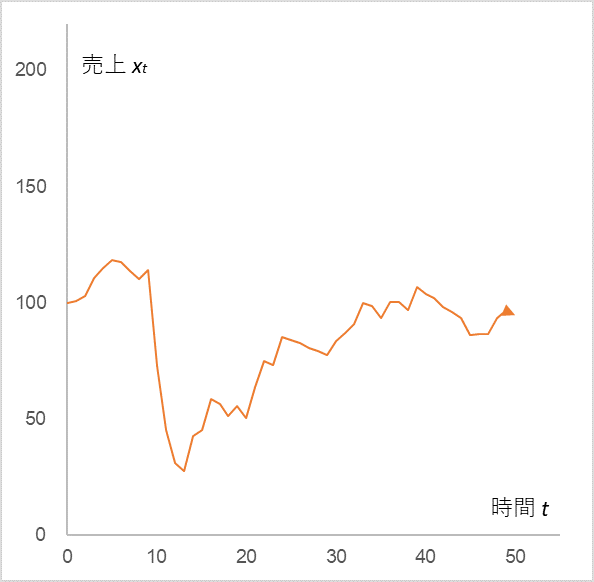
x₀=100, α=0.9. µ=10, ε_t は 図1と同じ正規分布に従うランダム項。但し、ε₁₀=-40, ε₁₁=-30, ε₁₂=-20,ε₁₃=-10

 

確かに、t₁₀ から t₁₃ の間に大きなマイナスの刺激を受けて売上は急落していますが、注目していただきたいのはそのあとです。いわゆるV字回復をしています。式（１）をみてください。売上係数 α が 1 以上であれば売上が上向くのは分かりますが、ここでは 0.9  で計算しています。ランダム項も t₁₀ から t₁₃ 以外は図１と同じ確率分布に従っています。とても不思議だと思いませんか？

そこで、なぜそうなるのかという理由が知りたくなります。分かりやすくするために式（１）からランダム項の ε_t を除きます。

$$x_{t}=αx_{t-1}+µ\tag{2}$$

ちなみに、ランダム項は線をギザギザにする役割しかありませんので、削除しても本質的な動きは変わりません。そして、式（２）に従って、実際、x₀, x₁, x₂, x₃ ・・・x_n がどうなるのかを調べてみます。

$$x_{0}$$

$$x_{1}=αx_{0}+µ$$

$$x_{2}=αx_{1}+µ=α(αx_{0}+µ)+µ=α^2x_{0}+αµ+µ$$

$$x_{3}=αx_{2}+µ=α(α^2x_{0}+αµ+µ)+µ=α^3x_{0}+α~2µ+αµ+µ$$

・

・

・

$$x_{t}=αx_{t-1}+µ=α^tx_{0}+µ(1+α+α^2+α^3+ ・・・+α^t)\tag{3}$$

 

となります。ここでようやく不思議の理由がみえてきます。時間 t が経過すると、α が 1 未満なので、α^tx₀  はゼロに近づきます。一方、1+α+α²+α³+・・・+α^t は、表１のように一定の値に収束します。

表１

α	0.9	0.8	0.7	0.6	0.5
1+α+α2+α3+・・・+αt	10.0	5.0	3.3	2.5	2.0

 

以上のことから、x_t は表１の 1+α+α²+α³+・・・+α^t を µ 倍した値に収束することがわかります。α=0.9 、µ=10 であれば、x_t は 100 に収束しますし、α =0.8、µ=10 であれば、50 に収束します。

ところで、収束値を決めるパラメーターが α と µ だけであって、初期値 x₀ に寄らないというのも興味深い点です。ちなみに、初期値を 0 → 100 → 200 と変えて計算をしてみると、

図３

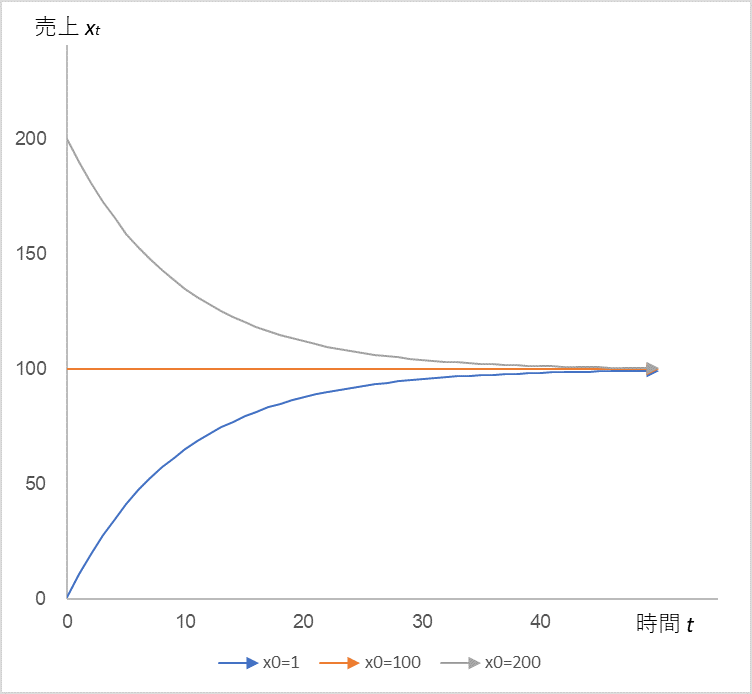
式（２）において、売上係数 α=0.9、定数 µ=10と固定し、初期値 x₀ = 1, 100, 200 の三通りで計算したときの売上 x_t の時系列変化

 

確かに、初期値にかかわらず売上 x_t は 100 に収束します。収束といえばロジスティック方程式

$$dx/dt=rx(1-\frac{x}{K})\tag{4}$$

を思い出しますが、そこには x が K に到達した時点で成長を止めてやろうという意志が感じられます（2021年5月6日付ブログの中の「上限のある成長」参照）。しかし、少なくとは私は、超単純な式（２）からはそのような意志を感じませんし、収束することすら予測ができませんでした。

式（４）では K が上限を決めるので、それが経営者目線に相当するとしました。一方、式（２）では、α と µ のコンビネーションによって上限が決まります。そこで、このふたつのパラメーターがそれぞれどのような役割をもっているのかをもう少しくわしく調べみましょう。

まず、µ を固定して、α だけを動かしてみましょう。

図５

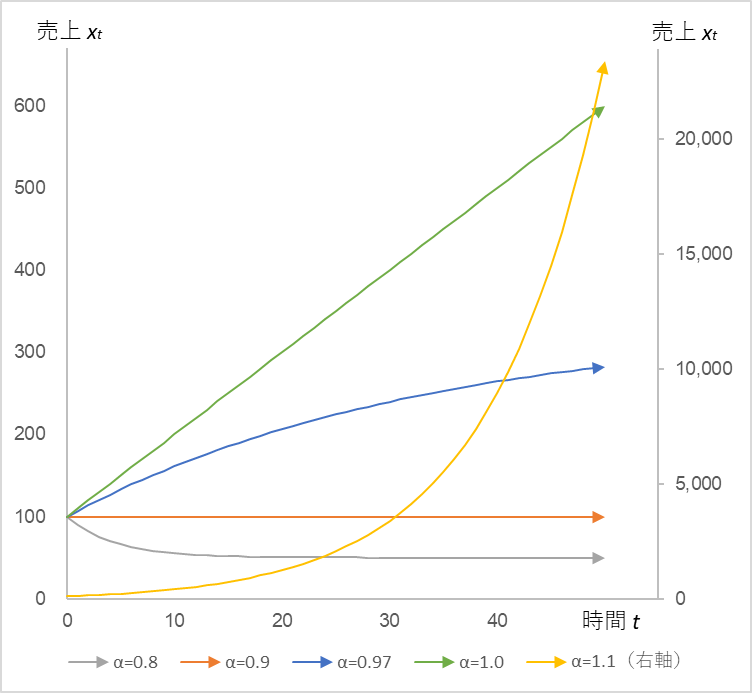
式（2）において、x₀ を100, µ を10 に固定して、α を 0.8 → 0.9 → 0.97 → 1.0 → 1.1 としたときの売上 x_t の時系列変化（α=1.1 のみ右軸）

 

売上 x_t が α に敏感に反応してます。α < 1 なら収束、α =1 で線形増加、α>1 で指数関数増加となり発散することがわかります。

次に、α を固定して µ だけを動かします。

図４

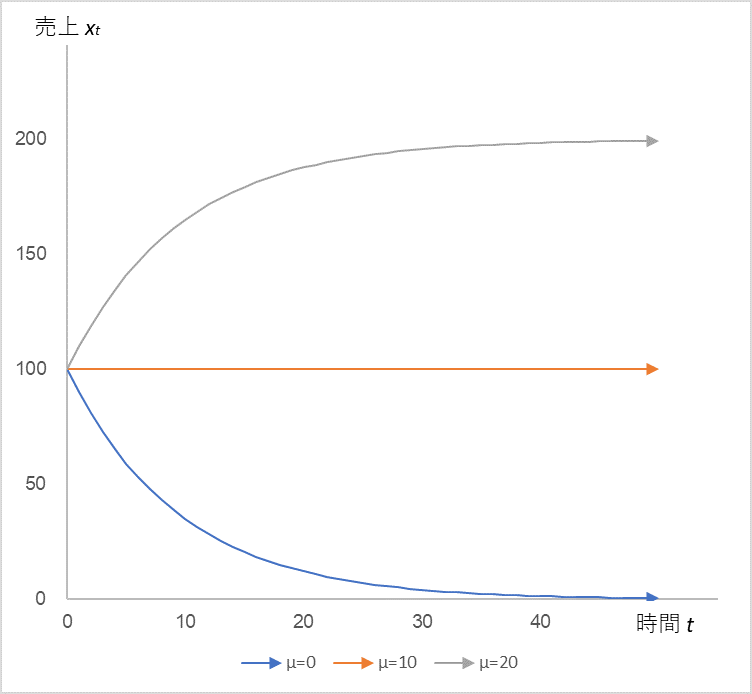
式（2）において、x₀=100、α=0.9 に固定し、µ=0 → 10 → 20 としたときの売上 x_t の時系列変化

 

ここでも売上 x_t が µ に敏感に反応しています。この前提条件において経営者が売上を安定させるためには µ を 10 以上の値に保つ必要があります。性質的にはロジスティック方程式の K に似ています。

以上より、「たとえマイナスの大きな刺激を受けたとしても、今までどおりのことをやり続けていれば必ずもとの状態にもどる」という、極めてシンプルな結論にたどりつきました。しかも、それには数学の裏付けがあります。心強いです。コロナの収束予測 も参考にしていただき、創意工夫とくじけない気力でなんとか切り抜ければ、売上はV字回復します。そしてそのつらい時期に行った創意工夫は α と µ の値を底上げしてくれるはずです。

「近い未来は過去よりも明るい」のです。

計算の詳細にご興味のある方は 時系列分析① – Excel をご覧ください。

 

時系列分析シリーズは、あと二回つづきがあります。

「継続は力なり」を数式で理解する（2021年9月11日付ブログ）

「経営者が目線を上げる、という数理的意味（2021年9月13日付ブログ）

 

＜参考文献＞

沖本竜義、AR過程、経済・ファイナンスデータの計量時系列分析、朝倉書店、2021

 

記事一覧へ戻る