本日は、2021年9月3日付ブログ「コロナ禍の売上急落の不安を払拭する超簡単な数式」と 2021年9月11日付のブログ「継続は力なりを数式で理解する」でご紹介した、超シンプルな数式に、実はもうひとつ経営の根幹にかかわる本質的な秘密が隠されていることをご紹介します。
まずは、その数式から。
$$x_{t}=αx_{t-1}+µ+ε_{t}\tag{1}$$
xt は時間 t における売上、 xt-1 はそのひとつ前の売上です。α は売上係数、µ は定数。εt は誤差項です。この単純な数式が、コロナ禍で落ち込んだ売上が必ずまた元の状態にもどること、逆に、一時的に急伸した売上もその後に何もしなければまたもとの状態にもどること、を教えてくれました。いずれも、式(1)の誤差 εt をマイナスに刺激したり、プラスに刺激したりすることで売上 xt の時系列変化をみてきました。
また、式(1)は、そのルールに基づき展開すると、式(2)に帰着し、
$$x_{t}=αx_{t-1}+µ+ε_{t}=α^tx_{0}+µ(1+α+α^2+α^3+ ・・・+α^t)+(α^{t-1}ε_{1}+α^{t-2}ε_{2}+α^{t-3}ε_{3}+・・・+ε_{t})\tag{2}$$
第一項: $α^tx_{0}$ は、$α<1$ のときゼロに近づく
第二項: $µ(1+α+α^2+α^3+ ・・・+α^t)$ は $α<1$ のときある一定の値に収束する
第三項の: $α^{t-1}ε_{1}+α^{t-2}ε_{2}+α^{t-3}ε_{3}+・・・+ε_{t}$ は係数のかかった誤差の集まりで正規分布する
というみっつの項に分解できる、そして、たとえばコロナ禍は、第三項の一部に大きなマイナスの刺激を与えることだし、逆に、一時的な売上の急伸は、大きなプラスの刺激を与えることでした。そして、いずれの場合も刺激が過ぎ去るともとの定常状態に戻る、だからコロナ禍はなんとか乗り切ろう、逆に伸びた売上をそのまま維持するためにはプラスの刺激を与え続けよう、というのが過去二回の結論でした。
さて、ここで式(2)をよくみると、売上 xt を底上げするのは第三項(誤差項)だけではないことがわかります。第二項の µ に注目してください。この µ が大きいか小さいかによって、収束する値が大きく変わります。むしろこちら方が売上へ本質的な影響を与えるといえます。つまり、この µ こそが経営者の目線なのです。
では早速、計算してみましょう。図1は、t=10 以降の µ を二倍の 20 に上げたときの xt の時系列変化です。
図1
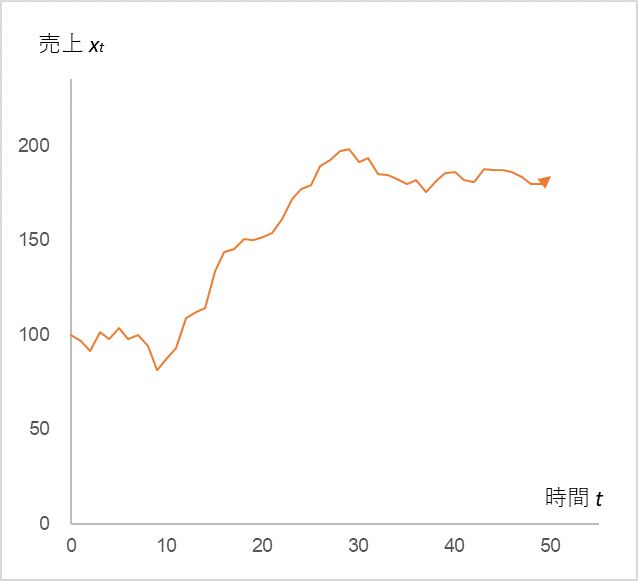
x0=100、α=0.9、εt=N(0,5) の正規分布とし、
t=10 以降の µ の値を 10 から 20に上げたときの売上 xt の時系列変化
確かに、経営者が目線 µ を二倍に上げたら、売上 xt も二倍になっています。ここで、さらに、t=10~13 に積極的な広告宣伝活動を行い、その後も継続したとします(図2)。
図2
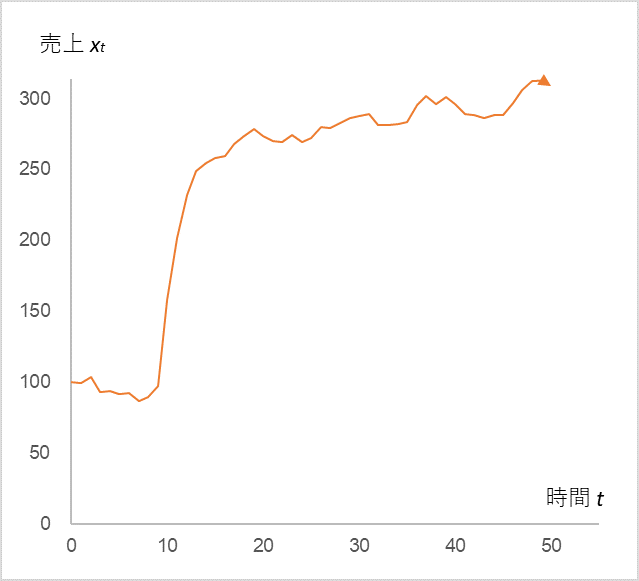
x0=100、α=0.9、ε0~10=N(0,5) , ε11~=N(10,5)
ε10=50, ε11=40, ε12=30, ε13=20
µ は t=9 まで 10、t=14 以降は 20
継続的な広告宣伝活動との「合わせ技」で売上が三倍になりました!
以上で、三回に渡る時系列分析シリーズはおしまいです。式(1)はとてもシンプルな形であるにもかかわらず、多くのことを我々に教えてくれました。
- 売上が一時的なマイナスの刺激によって落ち込んだとしてもまたもとに戻ること。
- 一時的な売上の上昇を維持するためには継続的な刺激(たとえば、広告宣伝活動など)が必要であること。
- 売上の底上げをするためには、経営者が現状のビジネスに満足することなく、目線を上げなければならないこと。
などです。これらのことは経験を通して肯定できそうな感じはしますが、絶対にそうか?と問われると例外もありそう、と腰砕けになってもおかしくはありません。しかしながら、今回行った一連の時系列分析によって、数学的な裏付けがあることがわかったわけですから、ここはもう自信をもってもいいでしょう。なんともいえない心強さを感じるのは、私だけでしょうか。
<参考文献>
沖本竜義、AR過程、経済・ファイナンスデータの計量時系列分析、朝倉書店、2021
記事一覧へ戻る