「世界一美しい等式」とは、オイラーの等式、
$$e^{i\pi}=-1\tag{1}$$
のことです。ネイピア数の $e$ を $i\pi$ 乗したらマイナス $1$ になる、という奇跡としか言いようのない等式です。ネイピア数 $e=2.71828…$ と、円周率 $\pi=3.14159…$ というどちらも終わりのない数が、実体のない虚数 $i$ に仲立ちされると、$-1$ という極めてシンプルな数になります。しかも、$+1$ ではなく、なぜか $-1$ です。ちなみに虚数 $i$ を除いて計算してみましょう。
Excel関数で $e$ の乗数を計算することができますが、 =EXP と入力すると、EXP(数値)と出てきて、具体的な数値を入れよと指示してきます。仮に、=EXP(3.14159) と $\pi$ の値を途中まで入力すると、23.14063 という数字を返します。が、Excelで計算できるのはここまでなので、ウィキペディアを参照すると、
$$e^{\pi}=23.1406926327…\tag{2}$$
と無限に続く正の数で、 ゲルフォントの定数と呼ばれているようです。いずれにしても、これで式 $(1)$ の右辺がマイナスになるのは虚数 $i$ の仕業であることがわかります。
さて、虚数が登場したときはおそらく $0$ が登場したときと同じような違和感があったと想像されます。数字は実体のあるものを数えるものであって、なにもない状態に数字を当てはめてなにがうれしいのか?という議論と、二乗したら $-1$ になる数なんてそもそもないのに、なぜそこまで数字を拡張する必要があるのか?という議論は本質的なところで似ているからです。今日、$0$ が必要なことは誰もが認めているわけですから、虚数 $i$ もそうあるべきなのかもわかりません。ただ、これは $0$ 円だ!と誰かが叫べば、それがタダであることが分かりますが、これは $i$ 円です、と言われても、「何それ?」ですので、われわれ一般人が普段みかけることのない $i$ にありがたみを感じることはなさそうです。そこが $0$ と大きく違うところです。
では、虚数 $i$ のありがたみはどこで感じることができるのでしょう?日常生活で遭遇しないのであればやはり数学の世界に入っていくしかありません。
中学三年生のときに習う二次方程式は、
$$ax^2+bx+c=0\tag{3}$$
という形をしています。この等式を満たす $x$ は次の二次方程式の解の公式を使うとすぐに見つけることができます。
$$x=\frac{-b±\sqrt{b^2-4ac}}{2a}\tag{4}$$
ここで、$a$, $b$, $c$ をシンプルにすべて $1$ とすれば、式 $(3)$ は、
$$x^2+x+1=0\tag{5}$$
になります。二次方程式の解の公式 $(4)$ を使って計算すると$x$ は、
$$x=-0.5±\frac{\sqrt{-3}}{2}\tag{6}$$
となります。二乗して $-3$ になる数はないので、中学では「この方程式には解がない」と学びます。式 $(6) をグラフにすると、
図1
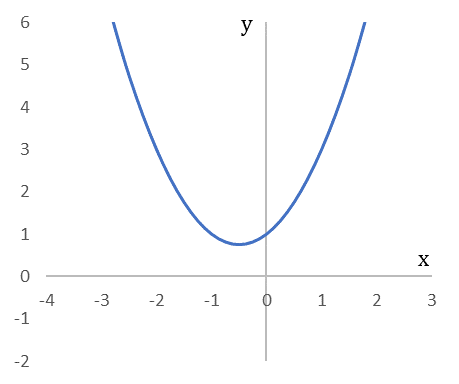
$x$ 軸と交わらない $y=x^2+x+1$ のグラフ
となり、確かに $x$ 軸と交わらないため式 $(5)$ を満たす $x$ がないことが視覚的にわかります。しかし、ここで諦めることなく、二乗して $-3$ になる数をつくってしまえば解があることになります。想像上でもいいから解が欲しい!という積極的な姿勢を示します。「想像上の」は英語で imaginary なので、その頭文字をとって $i=\sqrt{-1}$ と定義すれば、式 (6)は、
$$x=-0.5±\frac{\sqrt{3}}{2}i\tag{7}$$
と書けます。これを式 $(5)$ の左辺に代入すると、確かに右辺が $0$ になります。式 $(7)$ より、想像上の数字は、
$$実数±実数*i\tag{8}$$
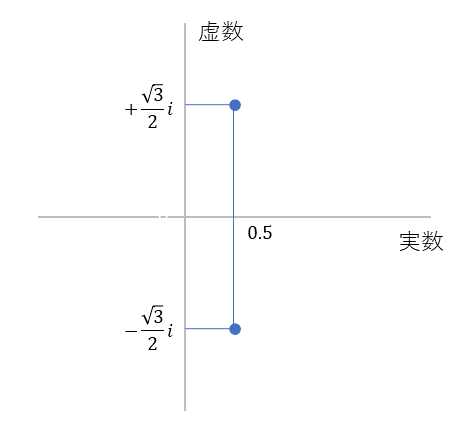
という実数と虚数が組み合わさった形をしています。式 $(7)$ を横軸に実数、縦軸を虚数にして、場所を確認してみましょう。
図2
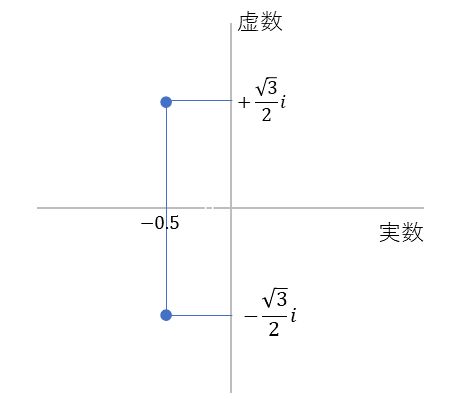
二次方程式 $x^2+x+1=0$ のふたつの解。横軸が実数、縦軸が虚数。
のように二か所にあることが目で見えるようになります。
実数軸と虚数軸に慣れるために、他のパターンもみておきましょう。
図3は $y=-x^2+x+1$ のグラフと $-x^2+x+1=0$ の解を図示したものです。グラフが $x$ 軸と交わるので実数解があり、実数軸上にふたつの解が現われます。
図3
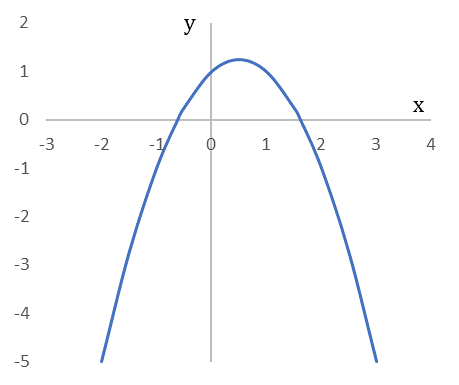
x軸と交わる $y=-x^2+x+1$ のグラフと $-x^2+x+1=0$ の解
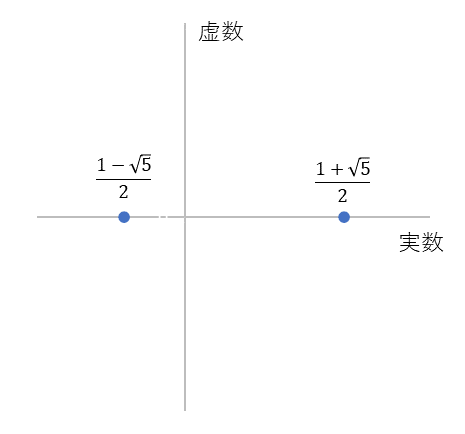
図4は $y=-x^2+x-1$ のグラフと $-x^2+x-1=0$ の解を図示したものです。グラフが $x$ 軸と交わらないので実数と虚数の組み合わせ解があることになります。
図4
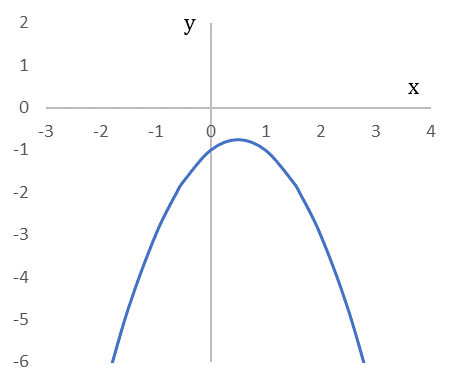
x軸と交わらない $y=-x^2+x-1$ のグラフと $-x^2+x-1=0$ の解
ここで注意すべきは、二次方程式のふたつの解は実数軸と虚数軸の単なる座標ではなく、実数軸に沿って動くベクトルと、虚数軸に沿って動くベクトルを足し合わせたベクトルだということです。
最初の二次方程式 $x^2+x+1=0$ にもどります。実数軸上と虚数軸上に示したふたつの矢印(ベクトル)の足し合わせが解の方向と場所を示しています。
図5
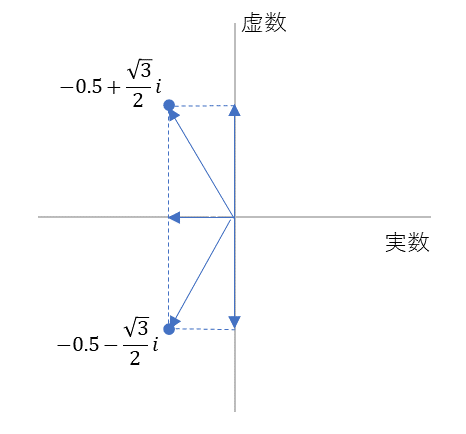
二次方程式 $x^2+x+1=0$ のふたつの解は、実数軸をマイナス方向に $0.5$、虚数軸を$±\frac{\sqrt{3}}{2}$ に動く
ふたつのベクトルを足し合わせたベクトルであって、単なる座標ではありません。
さて、ここでさらに発想の転換をします。この二次方程式のふたつの解を実軸と虚軸からの距離で特定するのではなく、実軸からの回転角度 $\theta$と原点 $0$ からの距離で特定してみましょう。
図6
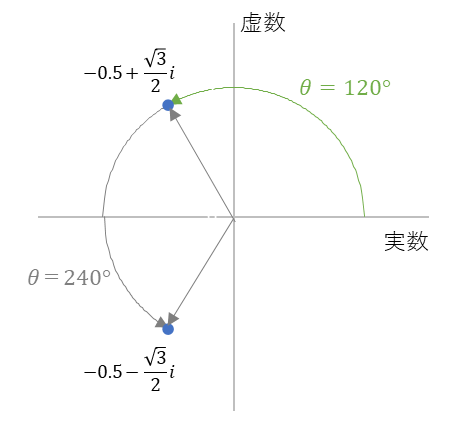
回転角度と原点からの距離による特定
二次方程式 $x^2+x+1$ の二つの解は、時計の針を3時の位置から反対方向に、120°と240°に回したところにあります。
角度といえばすぐに三角形が思い浮かびます。二等辺三角形の垂直の辺(高さ)を斜めの辺で割ったものがサイン、水平の辺(底辺)を斜めの辺で割ったものがコサインでした。三つの辺の長さは時計の針の角度によってさまざまに変化します。3時と9時の位置では垂直の辺(高さ)がなくなるのでサインはゼロ、12時と6時の位置では水平の辺(底辺)がなくなるのでコサインはゼロになります。
図7
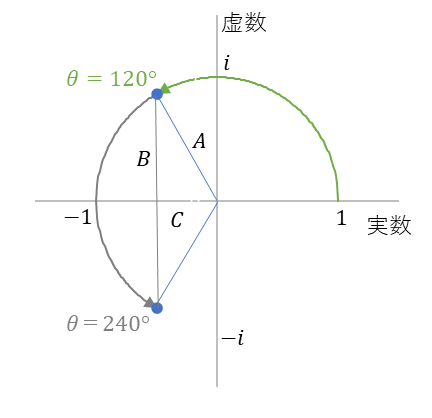
$\frac{B}{A}$ がサイン、$\frac{C}{A}$ がコサイン
サインは三時と九時の位置($\theta=0°、180°$) でゼロとなり、コサインは零時と六時の位置 ($\theta=90°、270°$) でゼロになります。
この二次方程式のふたつの解 $x$ は図2と同じように、虚数軸上に現れるサイン・ベクトル $\frac{B}{A}$と、実数軸上に現れるコサイン・ベクトル $\frac{C}{A}$ の足し合わせた場所にあります。つまり、
$$x=i\sin{\frac{2}{3}\pi}+\cos{\frac{2}{3}\pi}\tag{9}$$
$$x=i\sin{\frac{4}{3}\pi}+\cos{\frac{4}{3}\pi}\tag{10}$$
の二か所です。
ここで、たいへん重要なことに気が付きます。$\theta=180°$ つまり、$\theta=\pi$ のとき、$i\sin{\pi}+\cos{\pi}$ が $-1$ になります。ということは、世界一美しい等式 $e^{i\pi}=-1$ に辿り着くためには、$i\sin{\pi}+\cos{\pi}$ が、$e^{i\pi}$ に等しいことを示せばいいことになります。これは大きな発見です!
となると、次にやるべきことは、サイン、コサイン(三角関数)をネイピア数 $e$ に変換することです。さらなる飛躍が必要となりそうですが、シンプルに考えてみましょう。$\sin\theta$ も $\cos\theta$ も周期的な波です。つまり曲線の一種です。曲線といえば、多項式です。$y=x^2$ はカーブがひとつしかありませんが、$y=x^3$ になると二つに増えます。$y=x^4$ なら三つです。このように、どんどん累乗を増やしていけば三角関数を多項式に変換できそうです。
そこで、$\sin{\theta}$ を、
$$\sin{\theta}=a_{0}+a_{1}\theta+a_{2}\theta^2+a_{3}\theta^3+a_{4}\theta^4・・・\tag{11}$$
のように $\theta$ の多項式で書けると仮定します。式 $(10)$ に $\theta=0$ を代入すると、左辺は、$\sin{0}=0$、右辺は $a_{0}$ だけが残ります。よって、$a_{0}=0$ です。残りの定数、$a_{1}, a_{2}, a_{3}・・・$ はどうでしょうか。数学の世界には「困ったら微分」とか、「何はともあれ微分」ということばがあるようですので、とにかく式 $(11)$ を $\theta$ で微分してみましょう。
$$\cos{\theta}=a_{1}+2a_{2}\theta*3a_{3}\theta^2+・・・\tag{12}$$
となります。$\theta=0$ を代入すると、
$$\cos{0}=a_{1}$$
$\cos{0}=1$ なので、$a_{1}=1$ とわかります。 さらに、式 $(12)$ を $\theta$ で微分すると、
$$-\sin{\theta}=2a_{2}+3*2a_{3}\theta+4*3a_{4}\theta^2+5*4a_{5}\theta^3+・・・\tag{13}$$、
となり、$\theta=0$ を代入すると、
$$-\sin{0}=2a_{2}$$
つまり、$a_{2}=0$ とわかります。この操作を繰り返すと、$a_{3}, a_{4}, a_{5}・・・$ と芋づる式に定数を求めることができ、その結果が以下です。
$$\sin{\theta}=0+\theta-\frac{\theta^3}{2*3}+\frac{\theta^5}{2*3*4*5}-\frac{\theta^7}{2*3*4*5*6*7}+・・・\tag{14}$$
階乗の記号 $!$ を使って整理すると、
$$\sin{\theta}=\frac{\theta}{1!}-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+・・・\tag{15}$$
と少しすっきりします。同じ操作をコサインに対しても行うと、
$$\cos{\theta}=1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^56}{6!}+\frac{\theta^8}{8!}+・・・\tag{16}$$
になります。これで、サインとコサインを多項式で表すことができたので、これらを式 $(9)$ の右辺にどさっと代入します。
$$i\sin{\theta}+\cos{\theta}=i(\frac{\theta}{1!}-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+・・・)+(1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}+\frac{\theta^8}{8!}+・・・)\tag{17}$$
展開して整理すると、
$$i\sin{\theta}+\cos{\theta}=1+i\frac{\theta}{1!}-\frac{\theta^2}{2!}-i\frac{\theta^3}{3!}+\frac{\theta^4}{4!}+i\frac{\theta^5}{5!}-\frac{\theta^6}{6!}-i\frac{\theta^7}{7!}+\frac{\theta^8}{8!}+・・・\tag{18}$$
$i^2=-1$ を使って手直しすると、
$$i\sin{\theta}+\cos{\theta}=1+\frac{i\theta}{1!}+\frac{(i\theta)^2}{2!}+\frac{(i\theta)^3}{3!}+\frac{(i\theta)^4}{4!}+\frac{(i\theta)^5}{5!}+\frac{(i\theta)^6}{6!}+\frac{(i\theta)^7}{7!}+\frac{(i\theta)^8}{8!}+・・・\tag{19}$$
となります。これまでやったように微分を何度も繰り返したら極めてシンプルかつ規則正しい式 $(19)$ になる関数があるはずです。「微分、シンプル・・・」といえば、$e^x$ です。何回微分しても同じ $e^x$ だからです。実際にやってみましょう。
$$e^x=a_{0}+a_{1}x+a_{2}x^2+a_{3}x^3+a_{4}x^4・・・\tag{20}$$
と多項式に展開し、$x=0$ を代入すると、
$$e^0=a_{0}$$
つまり、a_{0}=1です。次に、式 $(18)$ を $x$ で微分すると、
$$e^x=a_{1}+2a_{2}x+3a_{3}x^2+4a_{4}x^3・・・\tag{21}$$
$x=0$ を代入すると、
$$e^0=a_{1}$$
つまり、$a_(1)=1$です。もう一度微分すると、
$$e^x=2a_{2}+3*2a_{3}x+4*3*a_{4}x^2・・・\tag{22}$$
$x=0$ を代入すると、
$$e^0=2a_{2}$$
つまり、$a_{2}=\frac{1}{2}$ です。
この操作を何度も繰り返して整理すると、
$$e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\frac{x^5}{5!}+\frac{x^6}{6!}+\frac{x^7}{7!}+\frac{x^8}{8!}+・・・\tag{23}$$
となります。ここで $x$ を $i\theta$ に置き換えると、
$$e^{i\theta}=1+\frac{i\theta}{1!}+\frac{(i\theta)^2}{2!}+\frac{(i\theta)^3}{3!}+\frac{(i\theta)^4}{4!}+\frac{(i\theta)^5}{5!}+\frac{(i\theta)^6}{6!}+\frac{(i\theta)^7}{7!}+\frac{(i\theta)^8}{8!}+・・・\tag{24}$$
となり、右辺が式 $(19)$ の右辺とまったく同じになります。右辺が同じなら左辺も同じなので、
$$e^{i\theta}=i\sin{\theta}+\cos{\theta}\tag{25}$$
が成り立ちます。$\theta=\pi$ とすれば、式 $(25)$ は、
$$e^{i\pi}=-1\tag{25}$$
となり、冒頭で紹介したオイラーの等式になります。
少し長い道のりでしたが、これで「世界一美しい等式」を導出することができました。
これまでの過程の中で、最大のポイントは図6~7だと私は思います。実数と虚数の組み合わせベクトルが単位円をぐるぐる回転する、その回転の途中にベクトルが $-1$ になる瞬間がある、それに気が付いたひとが「世界一美しい等式」を発見したのです。さぞびっくりしたことでしょう。
おわり
<追記>
もっと直感的に$e^{i\pi}$ がマイナス $1$ になることを理解するためには、$i$ を定義にもとづいて $\sqrt{-1}$ と表記してはどうでしょうか。
$$e^{\sqrt{-1}\pi}=-1$$
これなら、回転や微分を持ち出すまでもなく、なんとなくそうかなあ・・・という気がしてきませんか?見た目の美しさは今一つですが。
記事一覧へ戻る