When sales temporarily plummet for any reason, everyone feels a sense of psychological pressure. Moreover, we tend to have negative thoughts about when it will recover, or perhaps it will never recover. In particular, industries and stores that are still experiencing a drop in sales due to Corona are still wondering when they will be able to get out of this predicament.
Today, I would like to talk about a very simple formula that can dispel this anxiety. First of all, let’s look at the formula.
$$x_{t}=αx_{t-1}+µ+ε_{t}\tag{1}$$
Let’s assume that xt is the sales at time t. α is the sales coefficient, µ is a constant, and εt is the natural upward and downward motion of sales (random term). If you multiply the previous sales by a certain coefficient and add a constant and a random term, you get the current sales. How can this help you get rid of the anxiety from depressed sales? Whatever it is, let’s calculate it.
Let’s assume that sales x0 at t=0 is 100, the sales coefficient α is 0.9, and the constant µ is 10. Let’s assume that the random term εt follows a normal distribution with mean 0 and standard deviation 5. Then, the time series change of sales xt is shown in Figure 1.
Figure 1
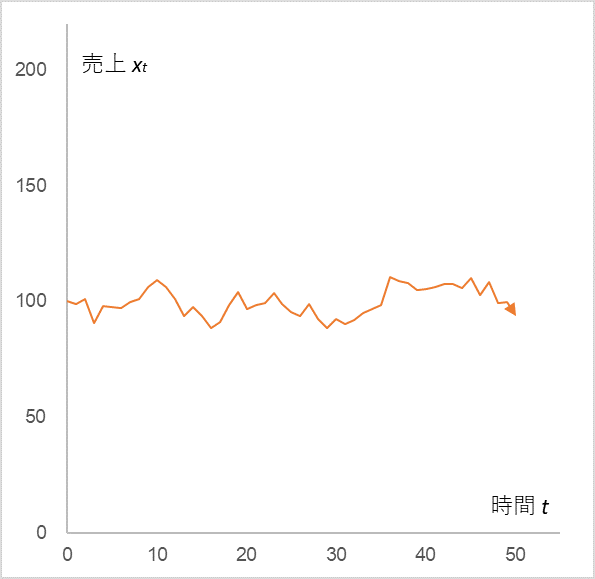
Initial sales x0=100, sales coefficient α=0.9, constant µ=10, random term εt= (probability normal distribution with mean 0 and standard deviation 5)
This is the sales trend when there is no COVID-19. Suppose that the corona arrives at t=10 to 13. To reflect this in the calculation, we force the values of the random terms ε10 to ε13 to be large negative values. Now, how will the sales change? See Figure 2.
Figure 2
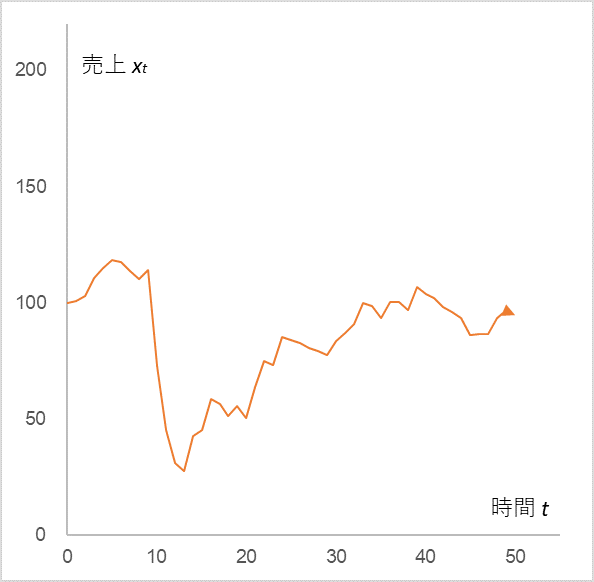
x0=100, α=0.9. µ=10, εt is a random term that follows the same normal distribution as in Figure 1.
ε10=-40, ε11=-30, ε12=-20, ε13=-10
It is true that sales plummeted due to a large negative stimulus between t10 and t13, but what we want you to pay attention to is what happened after that. But what you should pay attention to is what comes after that: the so-called V-shaped recovery. Look at equation (1). We know that sales will increase if the sales coefficient α is greater than 1, but here it is calculated at 0.9. The random term also follows the same probability distribution as in Figure 1 except for t10 to t13. Don’t you think this is very strange?
So, we would like to know the reason why this is so. To make it easier to understand, we will exclude the random term εt from equation (1).
$$x_{t}=αx_{t-1}+µ\tag{2}$$
Incidentally, the random term only plays a role in making the line jagged, so removing it will not change the essential motion. Then, according to Equation (2), let’s examine what actually happens to x0, x1, x2, x3, … xn.
$$x_{0}$$
$$x_{1}=αx_{0}+µ$$
$$x_{2}=αx_{1}+µ=α(αx_{0}+µ)+µ=α^2x_{0}+αµ+µ$$
$$x_{3}=αx_{2}+µ=α(α^2x_{0}+αµ+µ)+µ=α^3x_{0}+α~2µ+αµ+µ$$
・
・
・
$$x_{t}=αx_{t-1}+µ=α^tx_{0}+µ(1+α+α^2+α^3+ ・・・+α^t)\tag{3}$$
This is where the reason for the mystery finally becomes apparent. This is where the reason for the mystery finally becomes apparent. As time t passes, αtx0 approaches zero because α is less than 1. On the other hand, 1+α+α2+α3+… +αt converges to a constant value as shown in Table 1.
Table 1
| α | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 |
| 1+α+α2+α3+・・・+αt | 10.0 | 5.0 | 3.3 | 2.5 | 2.0 |
From the above, we can see that xt converges to the value obtained by multiplying 1+α+α2+α3+・・・・・・+αt in Table 1 by µ. If α = 0.9 and µ = 10, xt converges to 100, and if α = 0.8 and µ = 10, xt converges to 50.
By the way, it is interesting to note that the only parameters that determine the convergence value are α and µ, and they do not depend on the initial value x0. Incidentally, if we change the initial value from 0 to 100 to 200, we get
Figure 3
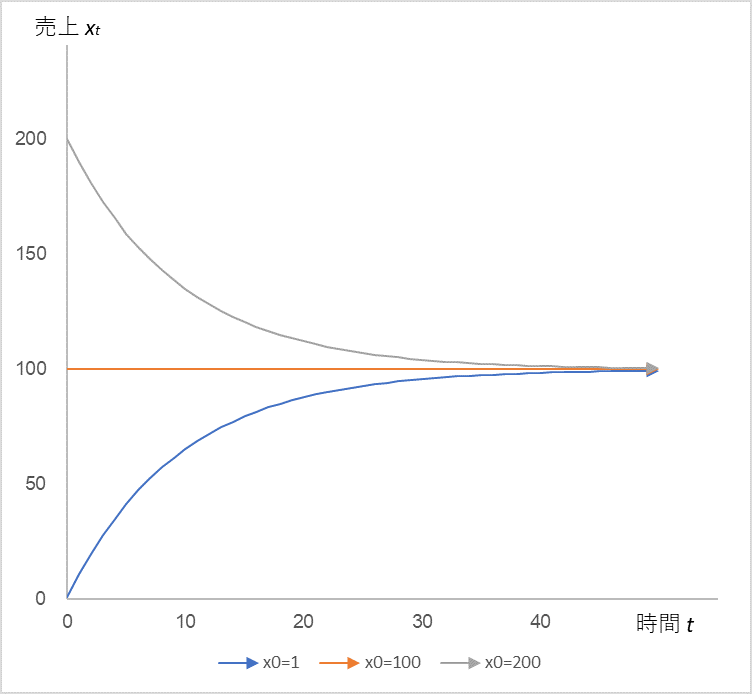
In Equation (2), the time series change of sales xt when the sales coefficient α = 0.9 and the constant µ = 10 are fixed, and the initial values x0 = 1, 100, and 200 are used.
Indeed, regardless of the initial value, the sales xt converges to 100. Speaking of convergence, the logistic equation,
$$dx/dt=rx(1-\frac{x}{K})\tag{4}$$
where there is a sense of will to stop growth when x reaches K (see “Growth with an upper bound” in my blog dated May 6, 2021). But at least I don’t sense such a will from the super-simple equation (2), and I couldn’t even predict convergence.
In equation (4), K determines the upper limit, which I assumed to be equivalent to the manager’s perspective. On the other hand, in Equation (2), the combination of α and µ determines the upper bound. Let’s examine the role of these two parameters in more detail.
First, let’s keep µ fixed and move only α.
Figure 4
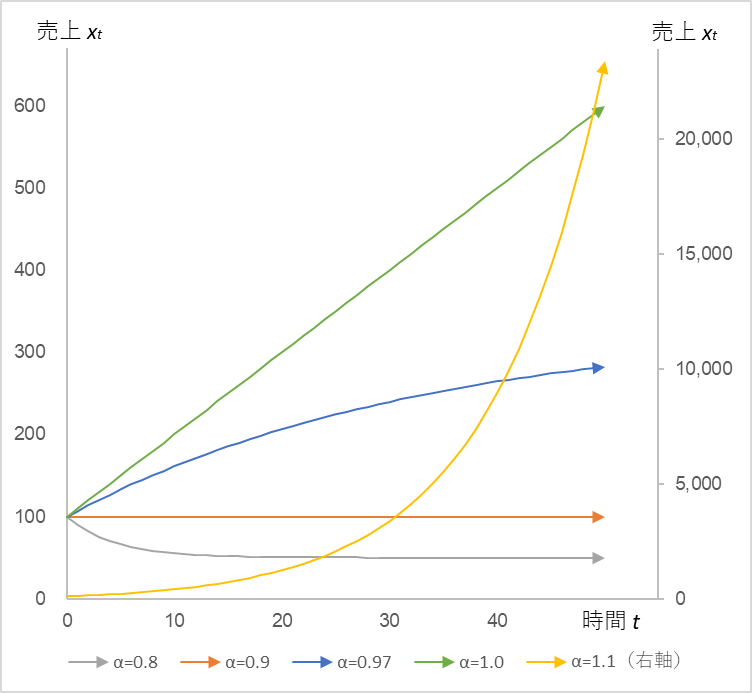
In Equation (2), when x0 is fixed at 100, µ at 10, and α is set to 0.8, 0.9, 0.97, 1.0, and 1.1, the time series of sales xt (right axis for α=1.1)
We can see that sales xt is sensitive to α: it converges when α < 1, increases linearly when α = 1, and diverges as an exponential increase when α > 1.
Next, we fix α and move only µ.
Figure 5
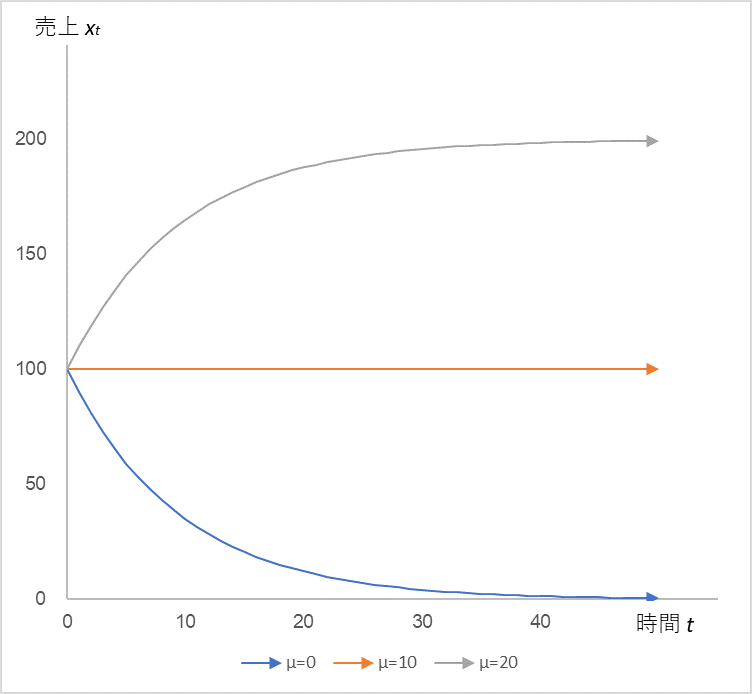
In equation (2), the time series change in sales xt when x0=100, α=0.9 is fixed, and µ=0 → 10 → 20
Here again, sales xt is sensitive to µ. Under these assumptions, the manager needs to keep µ above 10 in order to keep sales stable. It is similar in nature to the logistic equation K.
From the above, I came to a very simple conclusion: “Even if you receive a large negative stimulus, if you continue to do what you have been doing, you will always return to your original state.” Moreover, it is backed up by mathematics. This is reassuring. If you refer to the COVID-19 prediction of convergence and manage to get through it with ingenuity and perseverance, you will see a V-shaped recovery in sales. The ingenuity that you have shown during those difficult times will raise the values of α and µ.
The near future is brighter than the past!
If you are interested in the details of the calculation, please refer to Time Series Analysis (1) – Excel.
There will be two more installments in the Time Series Analysis series.
Understanding “Continuity is Power” with Formulas (blog dated September 11, 2021)
The Mathematical Meaning of “Managers Raising Their Eyes” (Blog, September 13, 2021)
<Reference>
Tatsuyoshi Okimoto, AR Process, Econometric Time Series Analysis of Economic and Financial Data, Asakura Shoten, 2021
The end
Back to archive