2022年6月17日付けのブログで、「円」を少しずつ変形して、「ハートマーク」を描き出せる数式を探しましたが、$x$ と $y$ の次数は $2$ どまりでした。本日は、その次数をさらに上げたらどうなるかをみます。

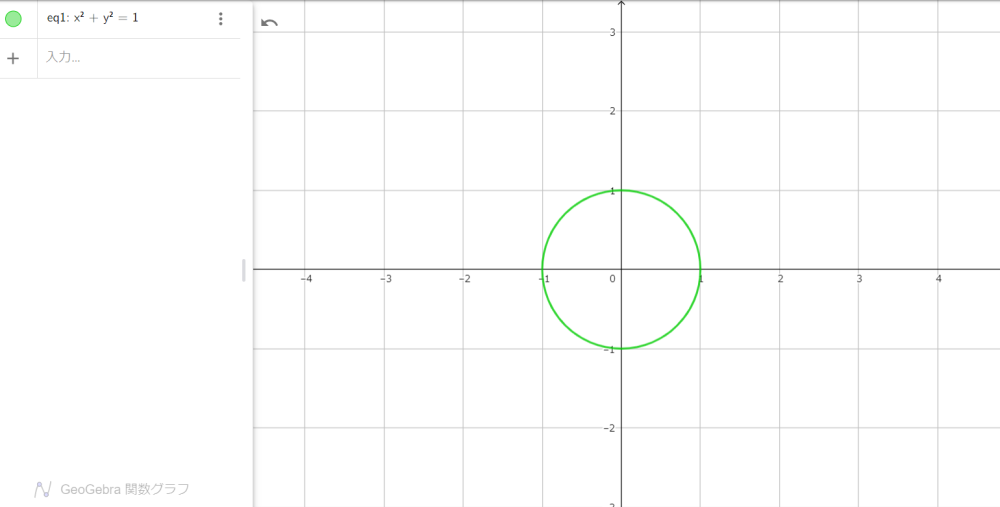
いつものように単位円からはじめましょう。

$$x^2+y^2=1\tag{0}$$

図０

まずは、$x$ の次数だけをひとつあげて $3$ にします。

$$x^3+y^2=1\tag{1}$$

図１

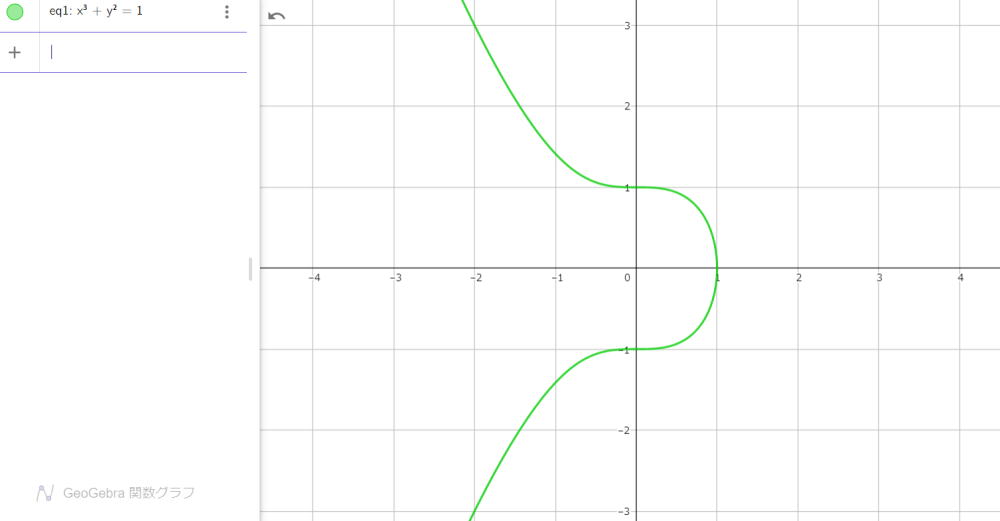
閉じた円から開いた曲線に変化しました。ここで、式 $(1)$ の右辺の $1$ を $0$ にすると、

$$x^3+y^２=0\tag{2}$$

図２

 

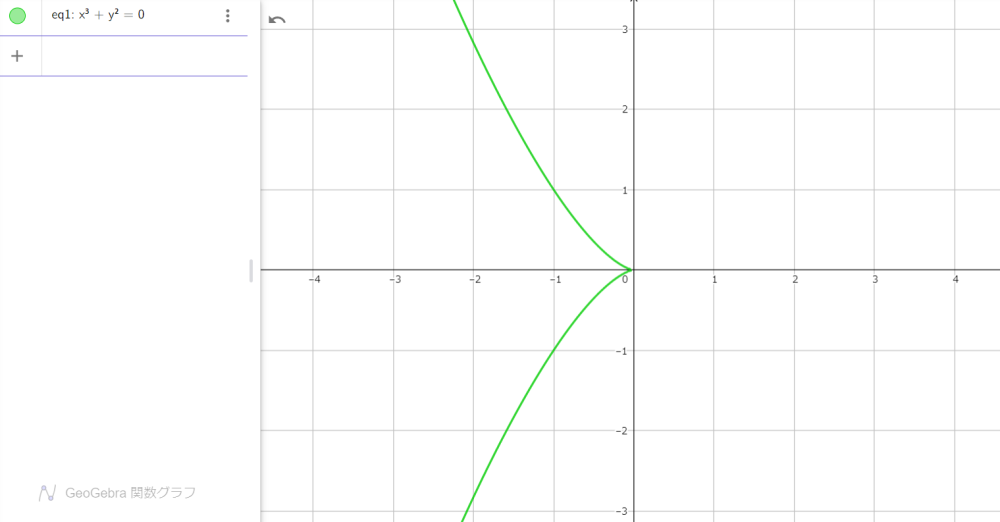
もはや円の面影はありません。ここで、式 $(2)$ の右辺 $0$ を $x$ に入れ替えてみましょう。

$$x^3+y^２=x\tag{3}$$

図３

 

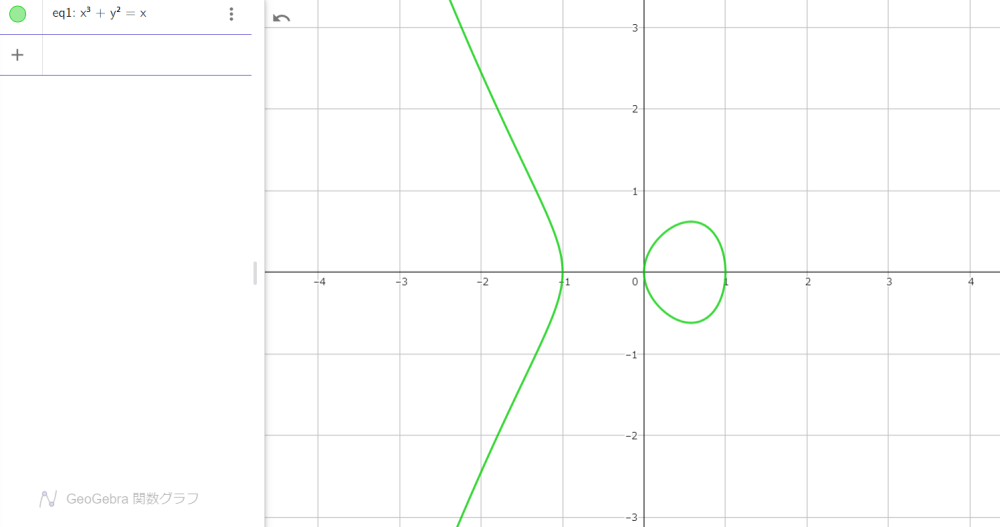
なんと、一本の曲線がふたつに分離して、そのうちのひとつはまた閉じた曲線になりました！首を横にしてみると、山頂から昇る朝日のようです。図２に比べると頂きはいい感じに丸みを帯び、大気の影響を受けた太陽の変形もなかなかリアルです。

座標中央部分にズームインしてみましょう。

図４

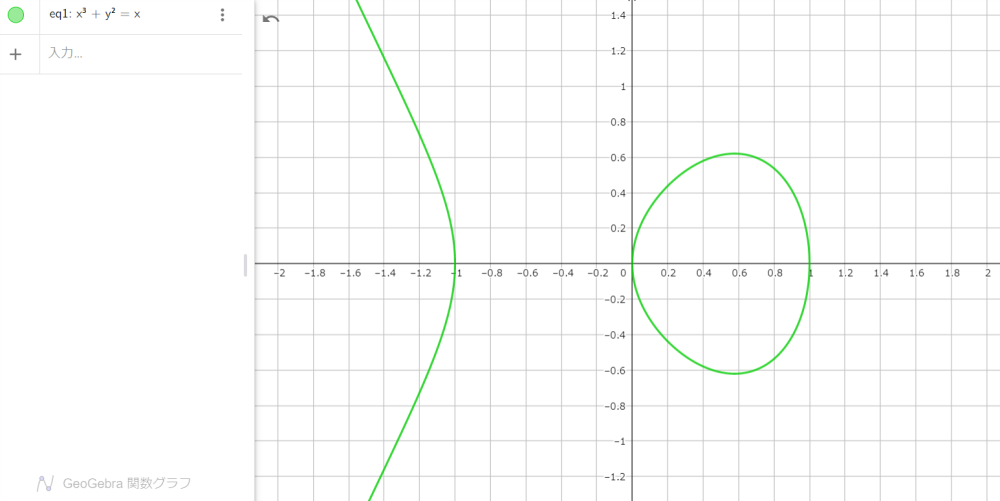
式 $(3)$ を変形すると、

$$y^2=x(1+x)(1-x)\tag{4}$$

ですから、

$$y=±\sqrt{x(1+x)(1-x)}\tag{5}$$

図４と式 $(5)$ からわかるように、「お山」と「お日様」に分離した曲線は、整数座標 $(x,y)=(-1,0)$ $(0,0)$ $(1,0)$ を通ります。また、式 $(5)$ によって、任意の $x$ の値における $y$ の値も計算できます。たとえば、$x=0.6$ のときは $y=±0.62$、$x=-1.2$ のとき $y=±0.73$ です （いずれも小数点以下第三位を四捨五入）。

 

次に、$y$ の次数も $3$ にあげて、数式の符号 $±$ と右辺の $x$ と $y$ に少しバリエーションをつけてみます。

$$x^3+y^3=x\tag{6}$$

$$x^3+y^3=y\tag{7}$$

$$x^3-y^3=x\tag{8}$$

$$x^3-y^3=-y\tag{9}$$

まとめて、$xy$ 座標に表示すると、

図７

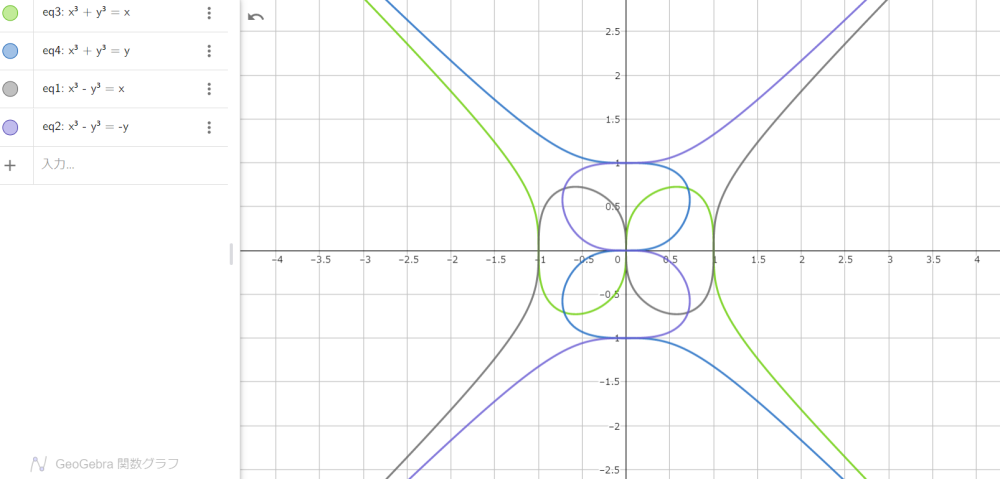
となり、四本の $S$ 字カーブが組み合わさった綺麗な模様になります。

さらに、$x$、$y$ 双方の次数を同時に $4$ へ上げてみます。

$$x^4+y^4=x\tag{10}$$

$$x^4+y^4=-x\tag{11}$$

$$x^4+y^4=y\tag{12}$$

$$x^4+y^4=-y\tag{13}$$

図８

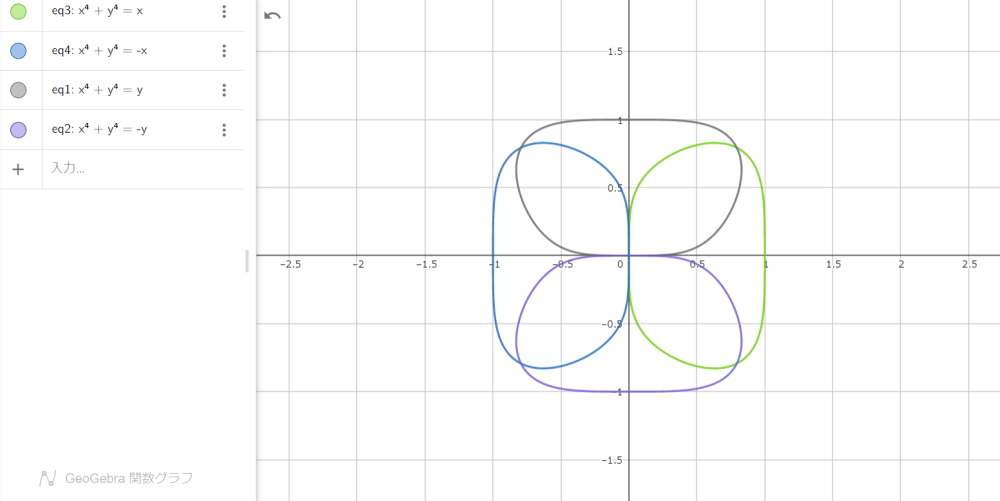
閉じた曲線になります。さらに次数をあげていくと、それらがそろって偶数であるかぎり、限りなく正方形に近づきます。図９は、

$$x^n+y^n=±x\tag{14}$$

$$x^n+y^n=±y\tag{15}$$

において、$n=10$ のときにできる模様です。

図９

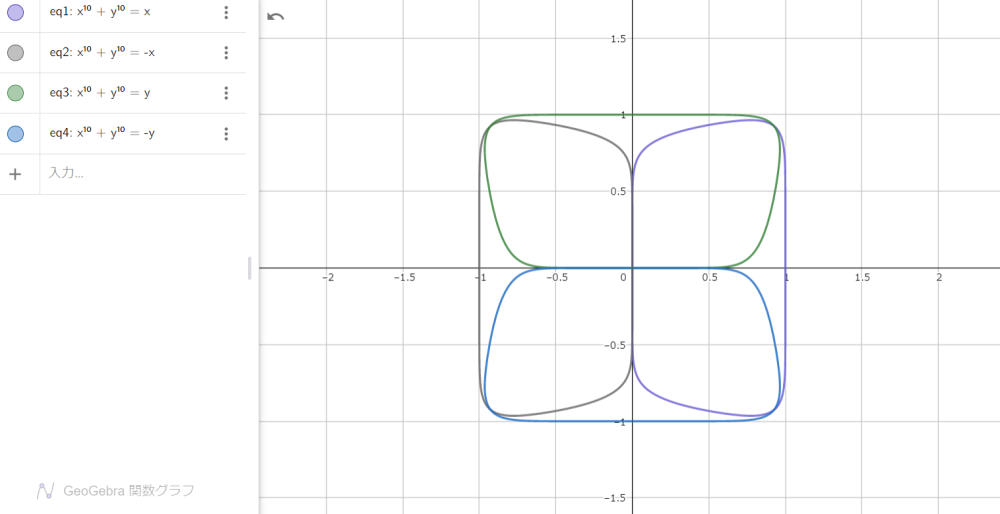
$n$ が偶数のとき、その次数をあげていくと、四つの角が鋭利になり、よつ葉の面積がひろがって、いずれは正方形に収束します。

 

単位円からはじまった今回の旅は、正方形に辿り着いたところでひとまず終了です。

 

振り替えると、美術的かつ数学的にもっとも興味深いのは図３の「非対称」な図形です。シンブルな数式、

$$x^3+y^２=x$$

が産み出すアートを、サムネイル画像2022年の富士山付近の初日の出（静岡新聞社）と合わせてご覧ください！

 

おわり

 

 

 

記事一覧へ戻る