厚労省から東京都の主要繁華街の夜間滞留人口が発表されています。期間は2020年3月1日から2021年6月11日まで、主要繁華街とは、上野仲町通、銀座コリドー街、六本木、新宿二丁目、歌舞伎町、渋谷センター街、池袋の七か所です。GPS移動パターンから職場と自宅の場所を推定したあと、職場・自宅以外の15分以上の滞留をレジャー目的としてカウントした、とあります。

一方、東京都からは新型コロナ・ウィルス感染者数が発表されていますので、このふたつを重ね合わせてみましょう。図1をご覧ください。

図1

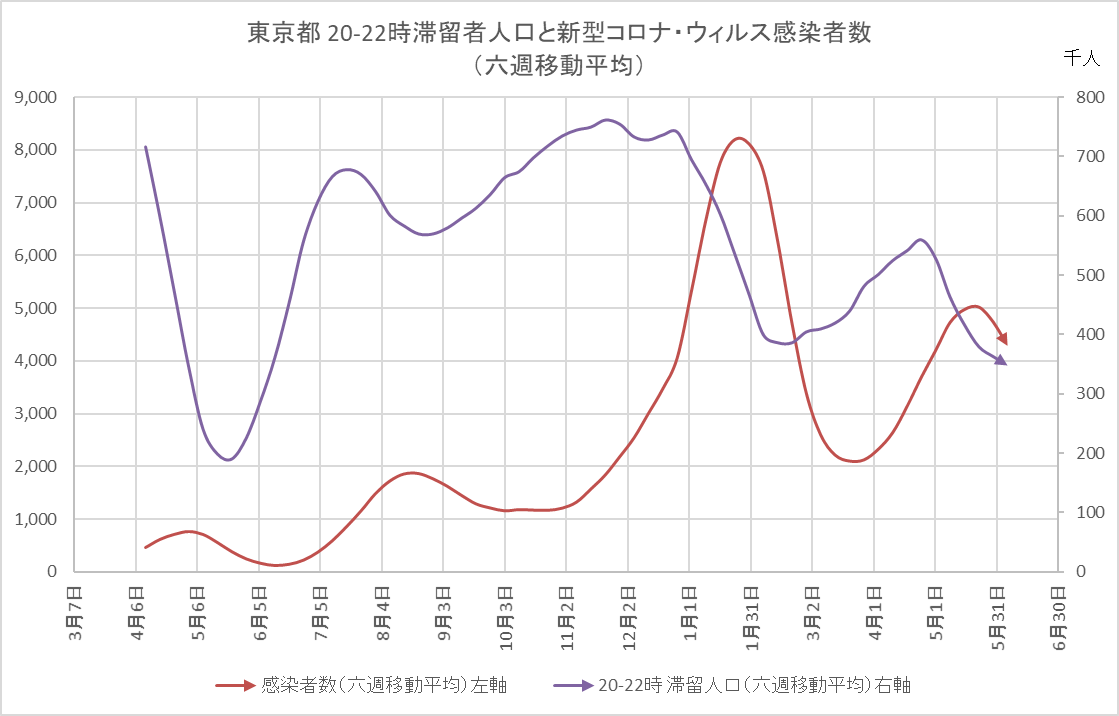
注）夜間滞留人口の元データが厚労省のウェブサイトに見当たらないため公表されているグラフから読み取りました。

 

感染者数が増えると夜の繁華街人口は減少し、感染者が減り出すとまた繁華街へ繰り出すという動きがみてとれます。

夜間滞留人口を縦軸に、感染者数を横軸にとって散布図に展開したものが図2です。ぐるぐる回転していて、ふたつは「うずまき関係」にあるようです。矢印は今後どこへ向かうのでしょうか？

図2

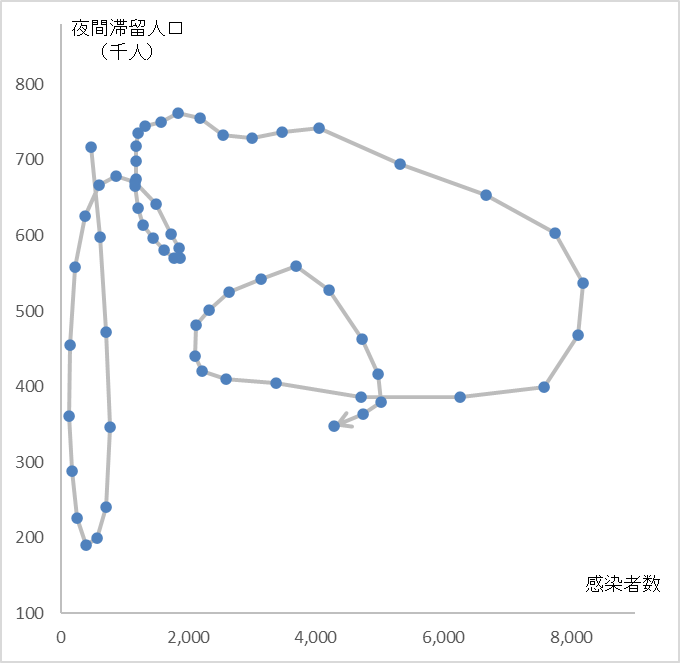
くるくると「うずまき」を描く、夜間滞留人口と感染者数の六週間移動平均

 

実は、数理生物学で有名な「うずまき関係」として「うさぎと山猫」の個体数の関係図があります。そのもとになっている数式が以下です。

$$\frac{dx}{dt}=rx(1-\frac{x}{K})-\frac{axy}{1+hx}\tag{1}$$

$$\frac{dy}{dt}=\frac{bxy}{1+hx}-cy\tag{2}$$ 

x はうさぎの数、y がうさぎを餌としている山猫の数です。係数は、r がうさぎの増殖率、K がうさぎの上限数、a がうさぎが山猫に出会って食われる速度、c は山猫の死亡率、b は山猫がうさぎを食って増殖する速度ですが、食べることができるうさぎの数に上限があるため 1+hx で割ってあります。

数式 (1) と (2) に表1 の係数を代入します。

表1

r	K	a	b	c	h
0.04	100	0.005	0.012	0.1	0.1

 

うさぎと山猫の初期値をそれぞれ 100 と1 にして、式 (1) と (2) で個体数がどう推移するか計算をすると図3のようになります。

図3

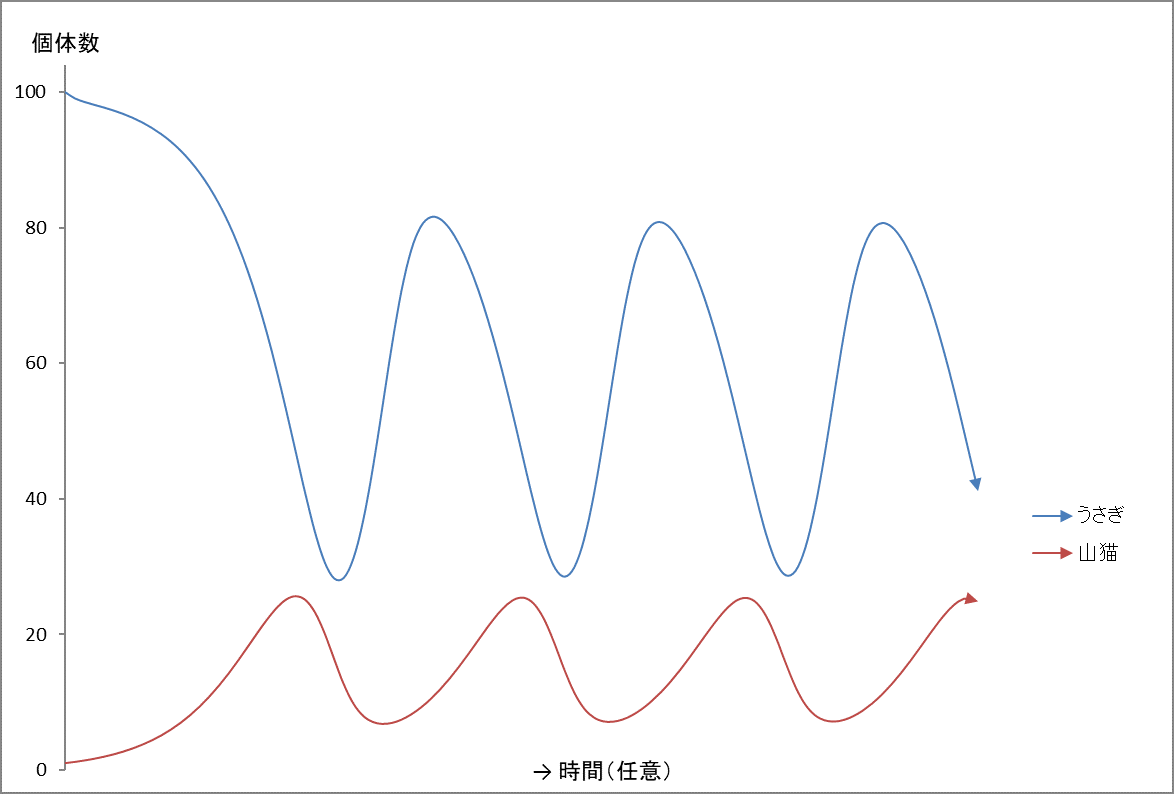
係数は表1の値。うさぎの初期値は 100、山猫は 1。

 

そして、これを散布図に展開すると、図4のようなきれいなサイクルが現われます。山猫の数が増えるとうさぎの数が減少し、餌のうさぎが減少すると、山猫が減少します。そうすると、今度はうさぎが増えます。これはとてもおもしろいサイクル現象で、数式が自然現象をみごとにあらわしていることにいたく感動しました。

ところが、教科書（数理生物学入門、巌佐庸著、2006）によると、「今のところ、野外の生物に見られる個体数の顕著な周期振動が捕食者と餌の相互作用によって生じていることがはっきりと確かめられた例はない。」とあります。これを読んで最初に受けた感動が一気にしぼみました。うさぎが減った理由は、山猫が増えたこと以外にも、うさぎの餌である草が減ったことも考えられるためです。

図4

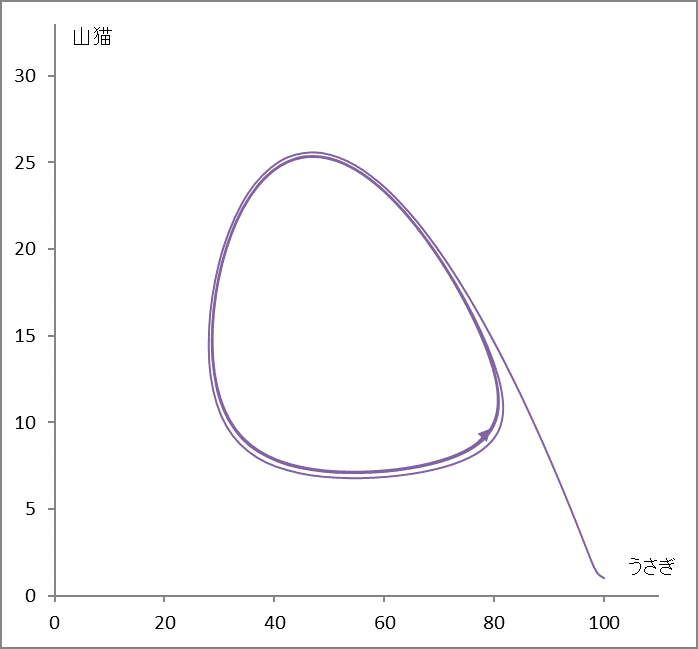
図3を散布図に展開するときれいなサイクル図になる！

 

さて、ここで、山猫をコロナ感染者、うさぎを夜間滞留者に置き換えてみます。うさぎと山猫のあいまいな関係とは違い、夜間滞留者の数が減るのは、コロナ感染者が増えたからという因果関係があることはあきらかですし、周期運動があることも図2が変則的ながらうずまきを描いていることからわかります。

ところで、式 (1) と (2）では、うさぎの数が多いと山猫のお腹がいっぱいになって摂食速度が遅くなるという前提が入っていましたが、コロナ・ウィルスの食欲が衰えるという話は聞きません。よって、式 (1) と (2）から 1+hx を削除しましょう。

$$\frac{dx}{dt}=rx(1-\frac{x}{K})-axy\tag{3}$$

$$\frac{dy}{dt}=bxy-cy\tag{4}$$

係数は表2を使い、修正した式 (3) と (4) を使って時系列変化を追ってみましょう。

表2

r	K	a	b	c
0.01	110	0.0002	0.0012	0.1

 

図5

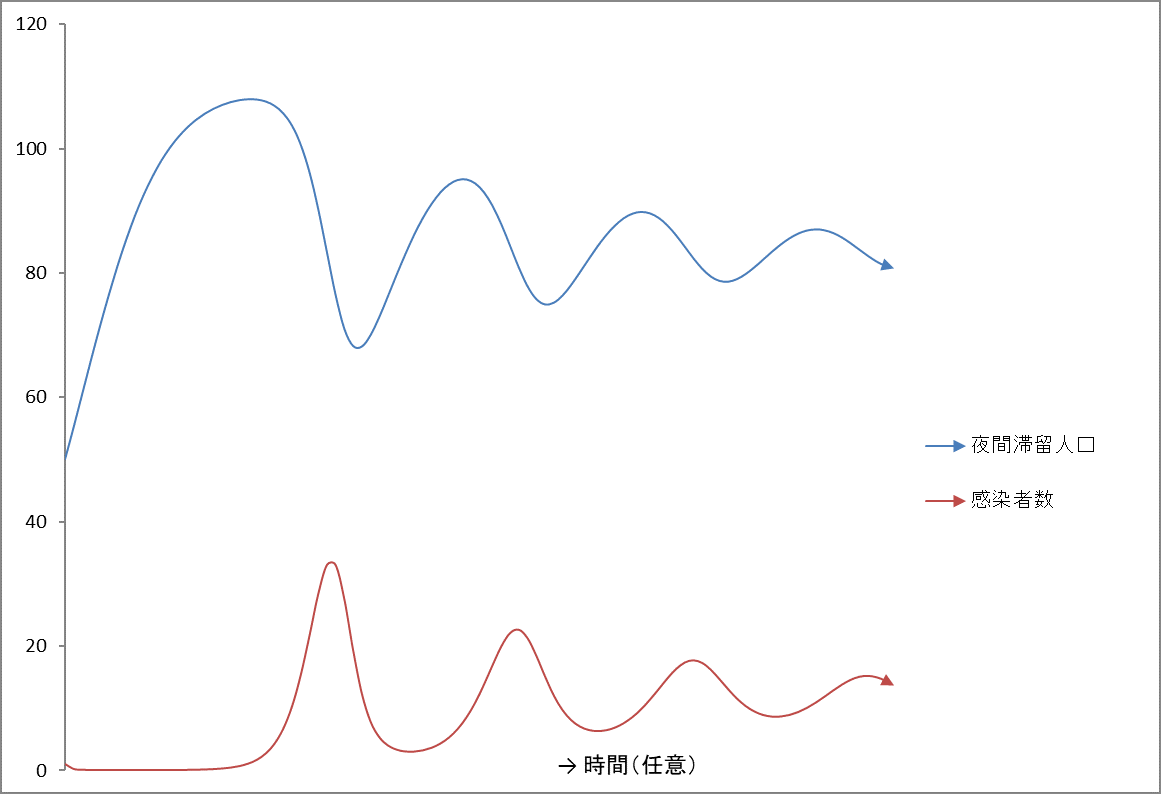
係数は表2より。夜間滞留人口の初期値は50、感染者数は1、とした。

 

感染者数と夜間滞留者数の波の振幅が徐々に小さくなっています。図5 を散布図に展開したものが図6 です。きれいな渦を巻きながら平衡点に収束する様子がみてとれます。まるでブラックホールに吸い込まれていくようです。

図6

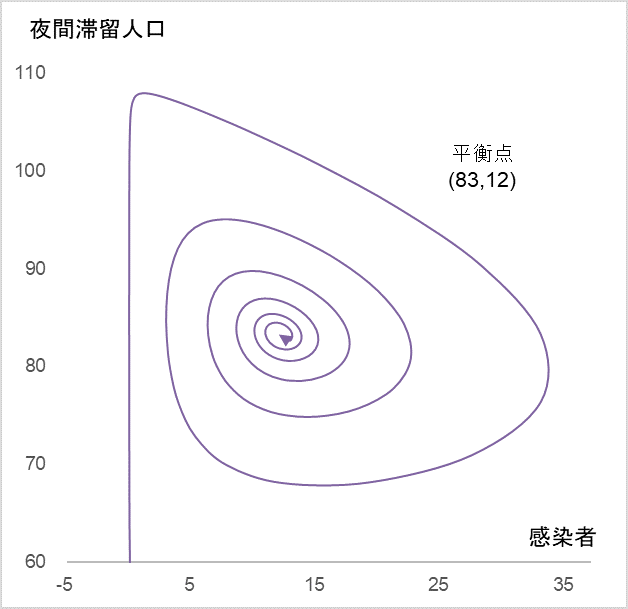
図5 を散布図に展開するときれいな「うずまき」になる。

夜間滞留人口と感染者数は平衡点 (83,12) に収束する。

 

このままではコロナ感染症はいつまで経ってもなくなりませんので、ここでワクチン接種の効果を加味します。今、「山猫＝感受性者にコロナ菌を感染させるひと y」ととらえていますから、ワクチン接種は y の数を減らすこと、つまり 係数 c の値を大きくすることを意味します。そこで、図6 で、夜間滞留人口と感染者の数が平衡点に近づいたのちに、係数 c の値だけを 0.1 から 0.13 と上げてみます。図7 をご覧ください。

図7

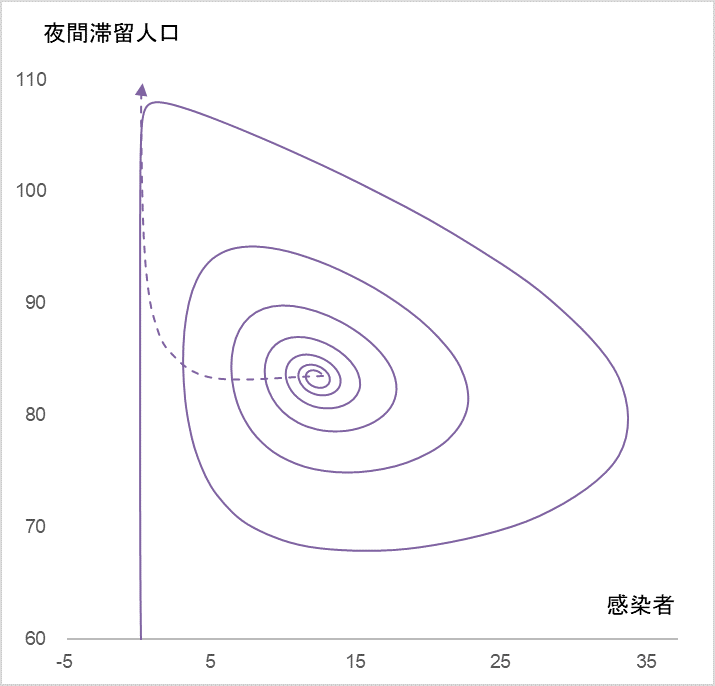
係数 c のみをを 0.1 から 0.13 へ上げたときの系のふるまい（破線部分）

平衡点から抜け出すことができる。

 

これでようやくもとの繁華街の賑わいを取り戻すことができます。これを現実の状況である図2 にあてはめてみると、ワクチン接種率が上がることによって矢印が今後、どこに向かうかをおおよそ予測できそうです。

引き続きモニターしていきましょう。

計算の詳細にご興味のあるかたは、リミットサイクル – Excel をご覧ください。

 

＜参考文献＞

巌佐 庸、捕食者と餌のサイクル、数理生物学入門、2006、37-38p

記事一覧へ戻る