COVID-19のワクチンが変異種にも効くのか効かないのか、が今話題になっています。三回目の接種をすすめたり、異種混合にしたりする国も出ていることから、同じワクチンでは徐々にその効果が薄れていくとみるのが妥当なようです。
しかし、そもそもウィルスはなぜ変異するのでしょうか。それはどうやらウィルスが増殖するときに発生する遺伝子のコピーミスが原因のようです。それが起こる確率は、理系YOUTUBER のヨビノリさんの動画「システム生物学④(動力学的校正)」によると10-4 、つまり一万分の一とのことです。翻訳エラーとはいえ、それがなければウィルスは進化できないわけですし、一度や二度、逃げ延びたとしてもいずれ免疫系につかまりますから、ずっと進化し続けなければならない運命にあるともいえます。つまり、ウィルスは絶えず免疫系よりも速く走らなければならない「命がけのかけっこ」を続けざるを得ません。
さて、この「かけっこ」を数学的に解析するのが本日のテーマです。ウィルスが変異するためのスペース(かけっこのためのトラック)を用意しておいて、自由に動いてもらうという考え方をするならば、地理的成長でみた「拡散項」を含む微分方程式が使えそうです。ここでは、「抗原エスケープモデル」(Sasaki, A. (1994). Evolution of antigen drift and switching – continuously evading pathogens. J. Theor. Biol., 168, 291-308 )を使って理解を深めます。
では、早速、数式をみてみましょう。 N は抗原(ウィルス)の密度、B は抗体の密度です。
$$\frac{∂N}{∂t}=[r-µ(1-p)]N-βNB+pu\frac{∂^2N}{∂x^2}\tag{1}$$
$$\frac{∂B}{∂t}=αNB\tag{2}$$
ここで、rはウィルスの増殖率、µ は突然変異率、p はその有効率、αとβ は免疫応答の強さを示す係数です。式(1)はウィルスが抗体によって攻撃されながらも、姿かたちを変えて生き延びようとする様子を、式(2)は抗体がウィルスを追いかける様子を表しています。
では、これらの数式に具体的な係数を入れて実際に計算をしてみましょう。スタート地点は、抗原N(ウィルス)、抗体 B ともに x12 です。初期密度は N を 0.01 、B は 0.001 とします。時間間隔 (⊿t)は 5.0 です。
その他の係数は以下としました。
| 抗原の増殖率 | r | 0.12 |
| 突然変異率 | µ | 10-4 |
| 有効変異率 | p | 0.5 |
| 免疫応答率 | α | 0.1 |
| 免疫応答率 | β | 0.1 |
縦軸は抗原 N と抗体 B の密度 D、横軸 x は変異型が現われるスペースです。時間を t=50 ごとに進めたときの動きは図1のようになります。
図1
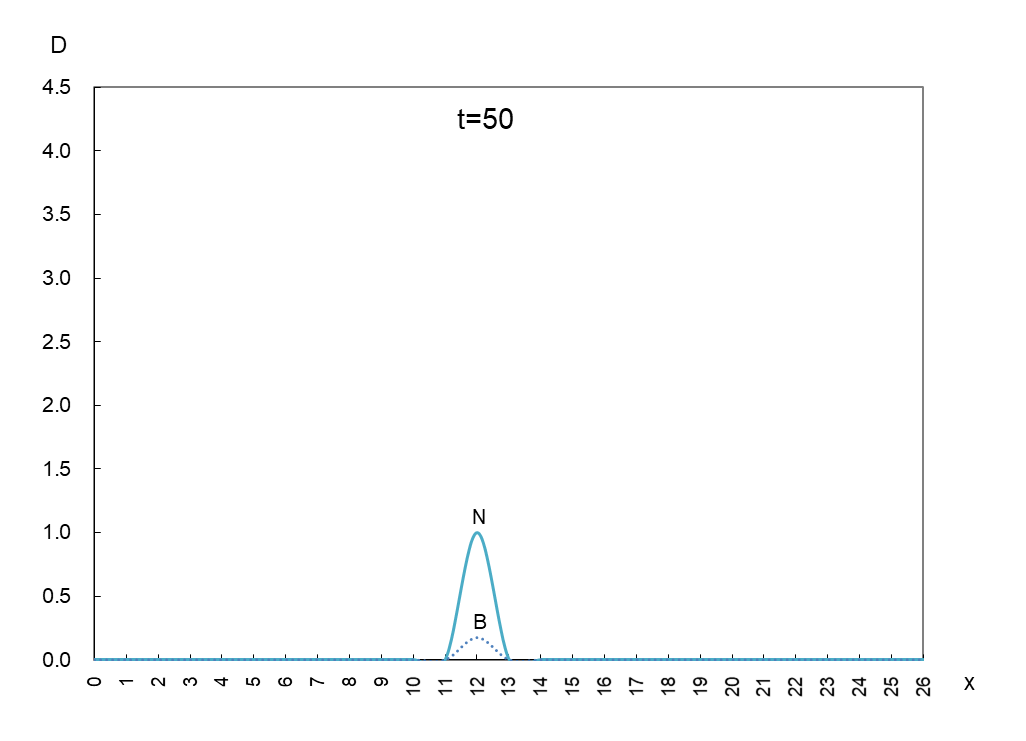
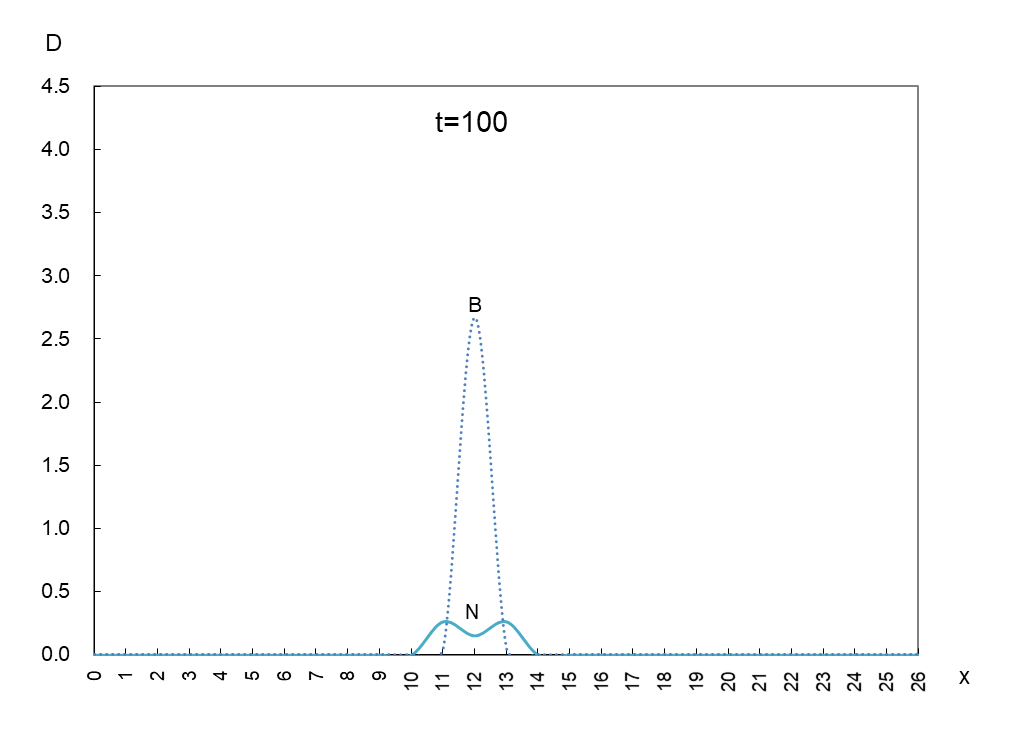
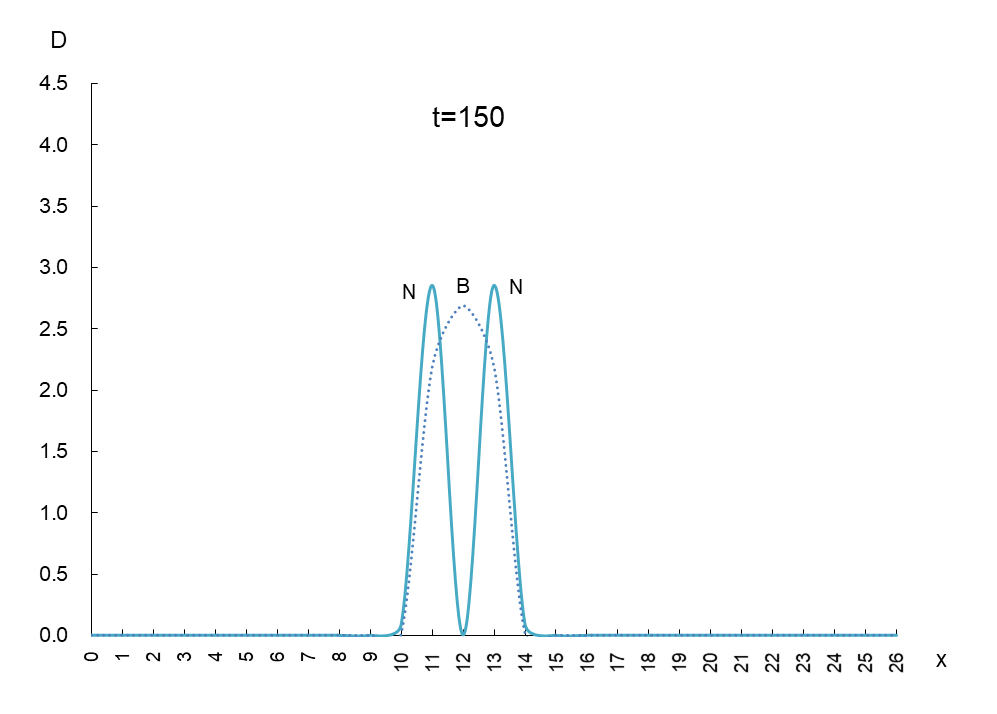

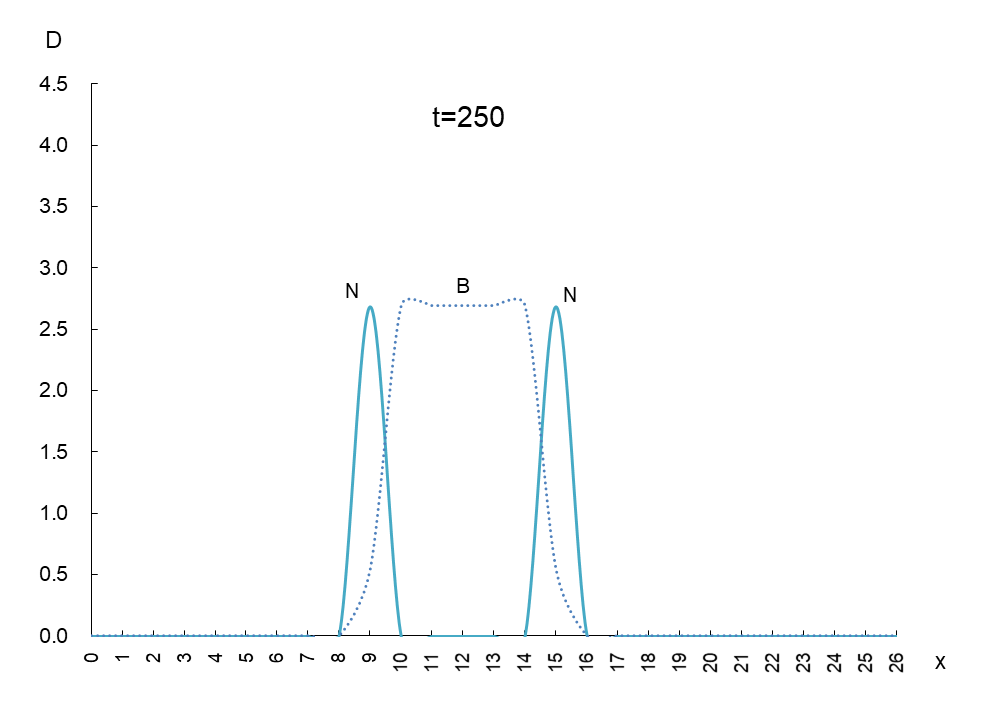
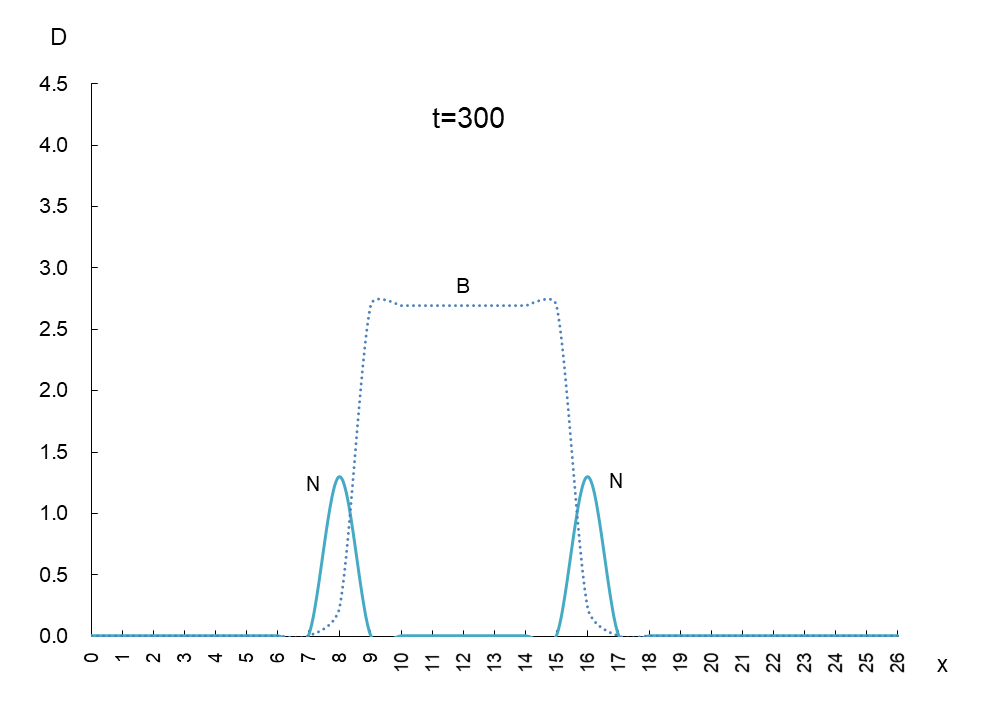
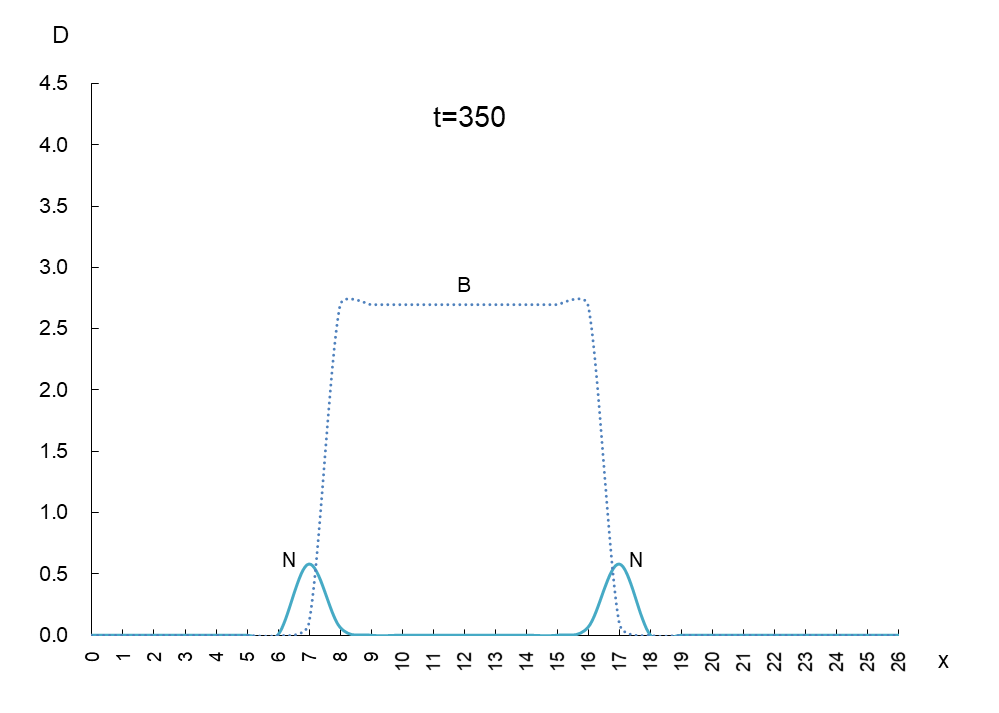
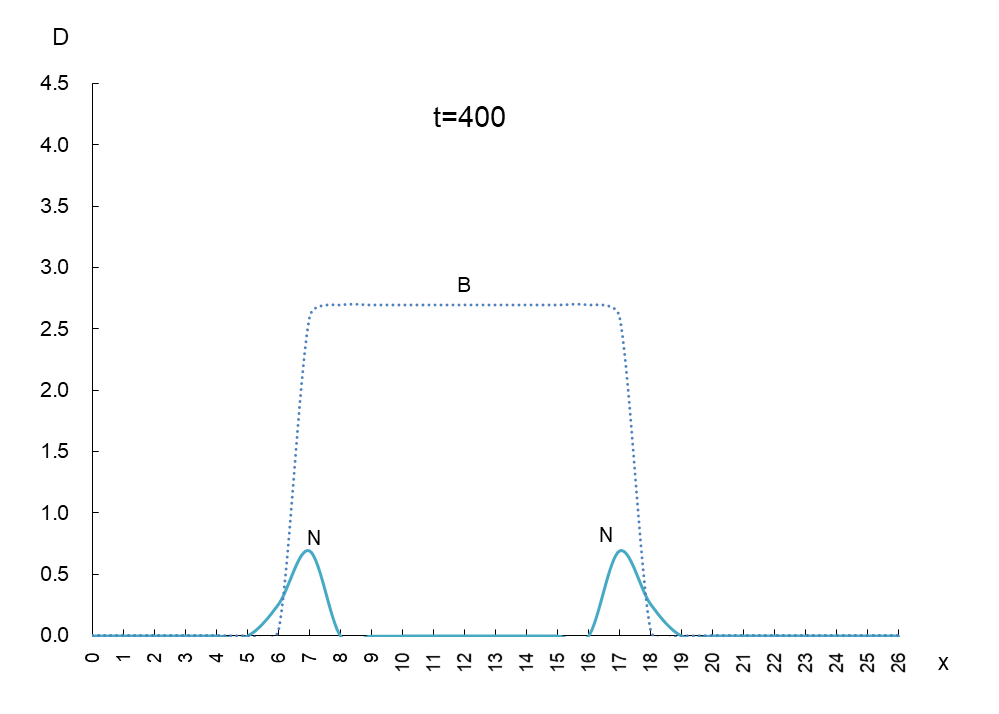
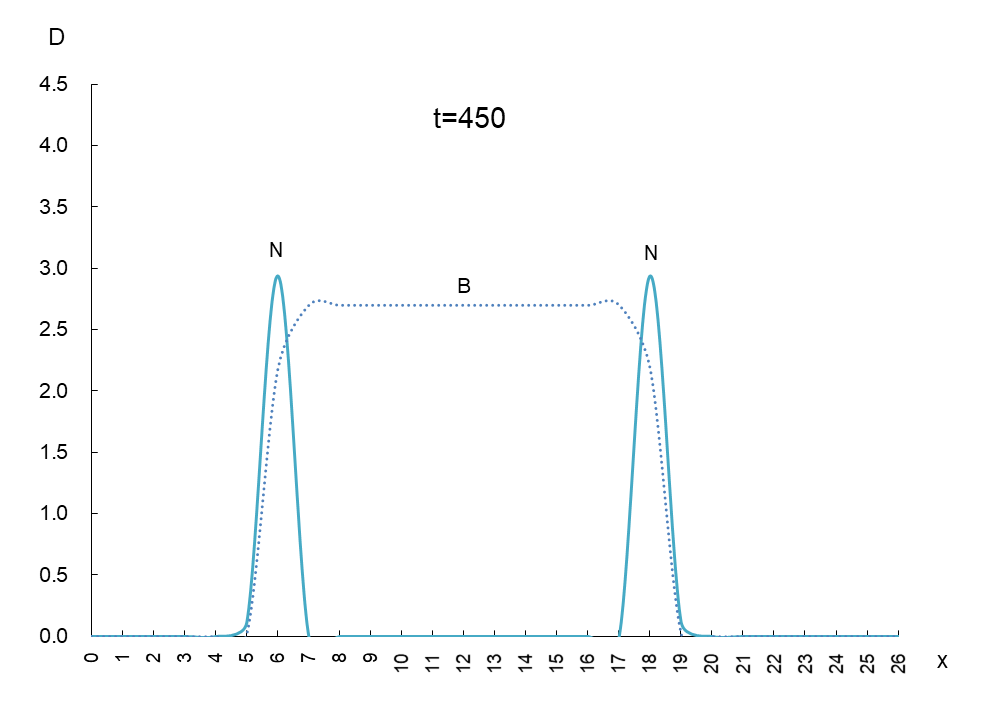
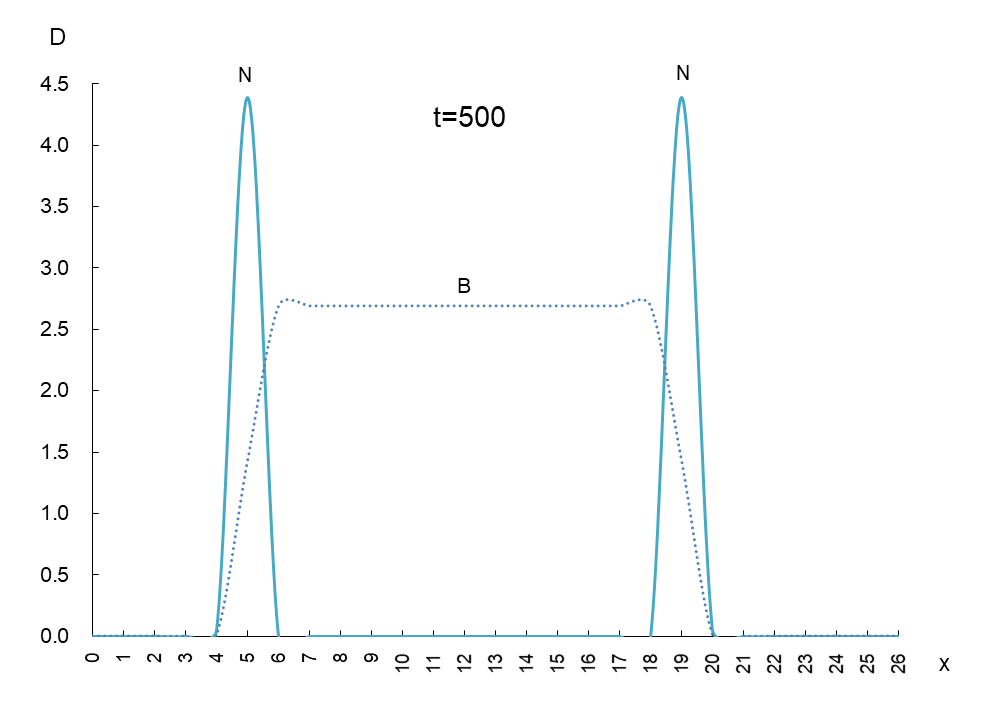
抗原 N (実線)と抗体 B(破線)の挙動を観察するため、少し多めに撮影しました。これらから読み取れることは、
① 抗原 N は確かに抗体 B から逃げている。
② 抗原 N は逃げながら増減(0.5~4.5)を繰り返しているが、抗体 B の密度(2.7)は一定である。
③ 抗原 N と抗体 B の移動速度は一定である。
などで、なかなか興味深い結果です。
では、ここで図1の横軸を時間 t にして、縦軸を抗原 N の密度にします。図2をご覧ください。抗原密度 N が時間経過とともに波打っています。
図2
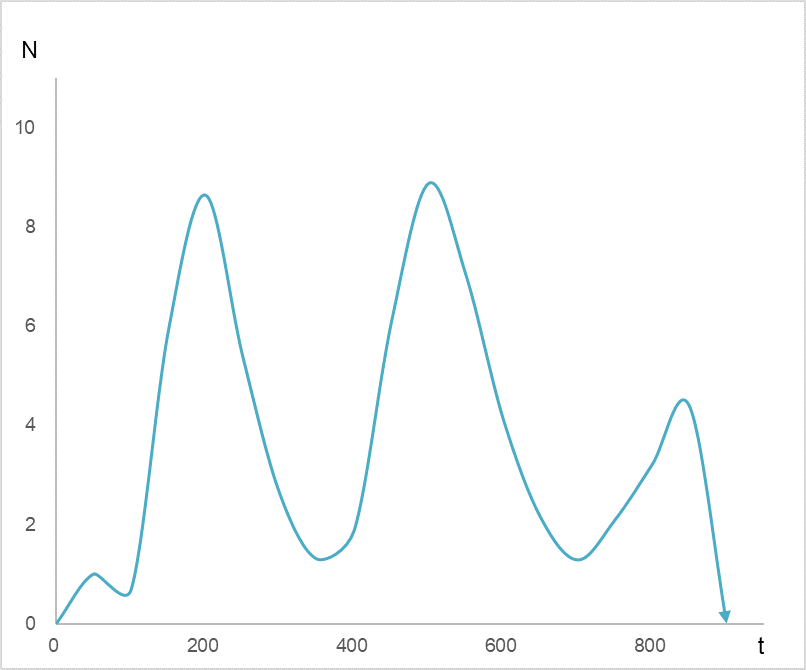
抗原密度 N の波打ち現象
当サイトで毎週、新型コロナ・ウィルスの収束予測をしています。2021年8月15日のブログでアップしたグラフが図3です。ドットは、厚労省から日次で発表されている感染者数を週別にプロットしたものです。
図3
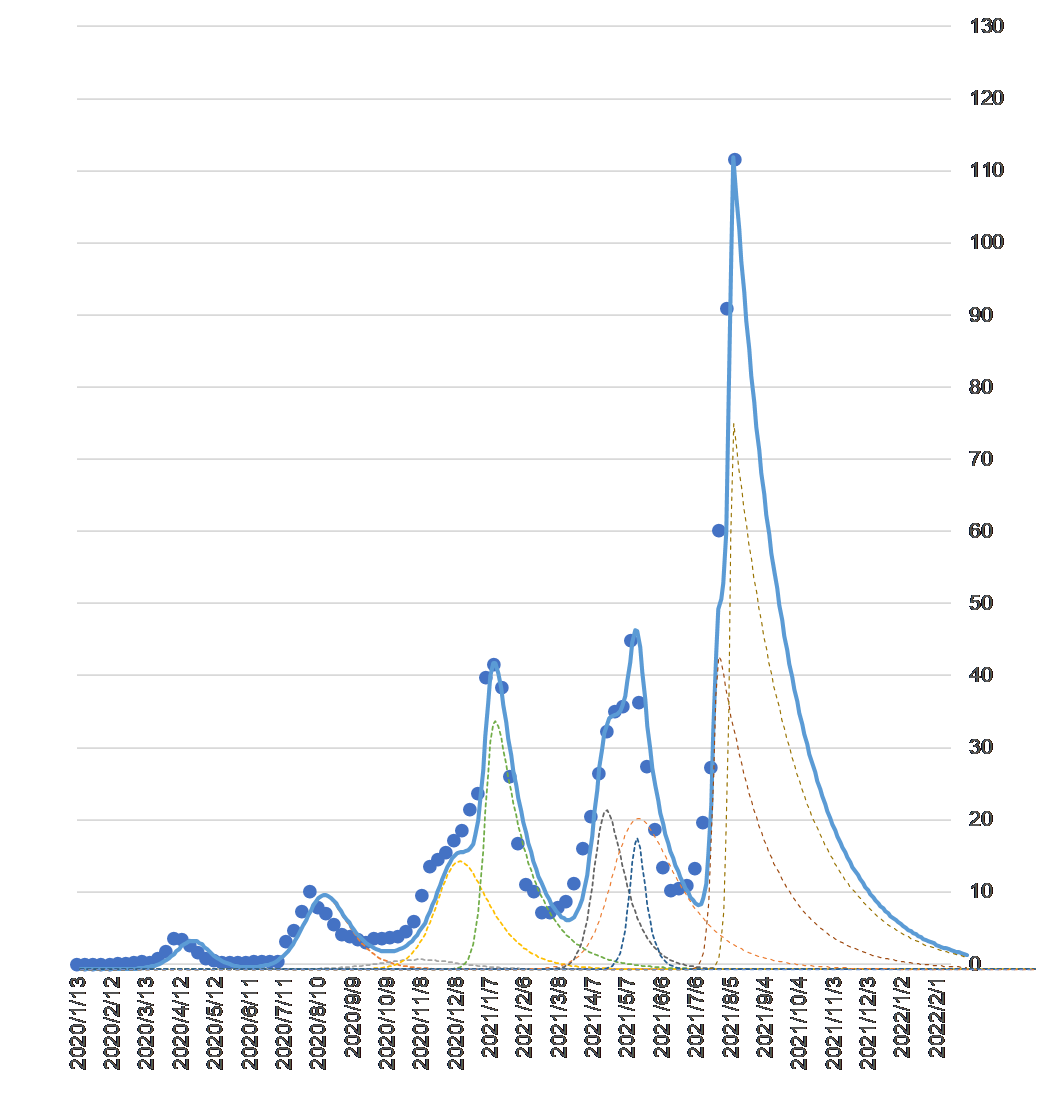
新型コロナ・ウィルスの感染者数(縦軸、単位:千人)の週別推移と合成波による収束予測
(図3のアップデート版は「新型コロナウィルス感染症収束予測の検証(アップデート中)」をご覧ください。)
各変異種の波が破線で表されています。その変異波の合成波が青色の実線です。実線が実際の感染者数にほぼ一致しているのは、そうなるように各変異種のパラメーターを調整しているからです(具体的な方法は2020年11月22日付のブログ をご覧ください)。
このときに使った数理モデルは、捕食者(ウィルス)が餌(人間)を食べるという視点でつくられた方程式(ロトカ・ボルテラ捕食系バージョン 2020年4月16日付ブログ )でしたが、今回使用した抗原エスケープモデルは、「ウィルスは抗体から逃げ続けなければならない」という視点で組み立てられています。それぞれ切り口は違いますが、実際の感染者数が波打つという現象をいずれも数理的に再現することができます。
計算の詳細にご興味のある方は、抗原エスケープモデル – Excel をご覧ください。
記事一覧へ戻る