厚生労働省の発表によると、先週（2022年8月1日～7日）に行われた新型コロナ・ウィルス検査の陽性者は約1.5百万人で過去最高に達しました。

図１

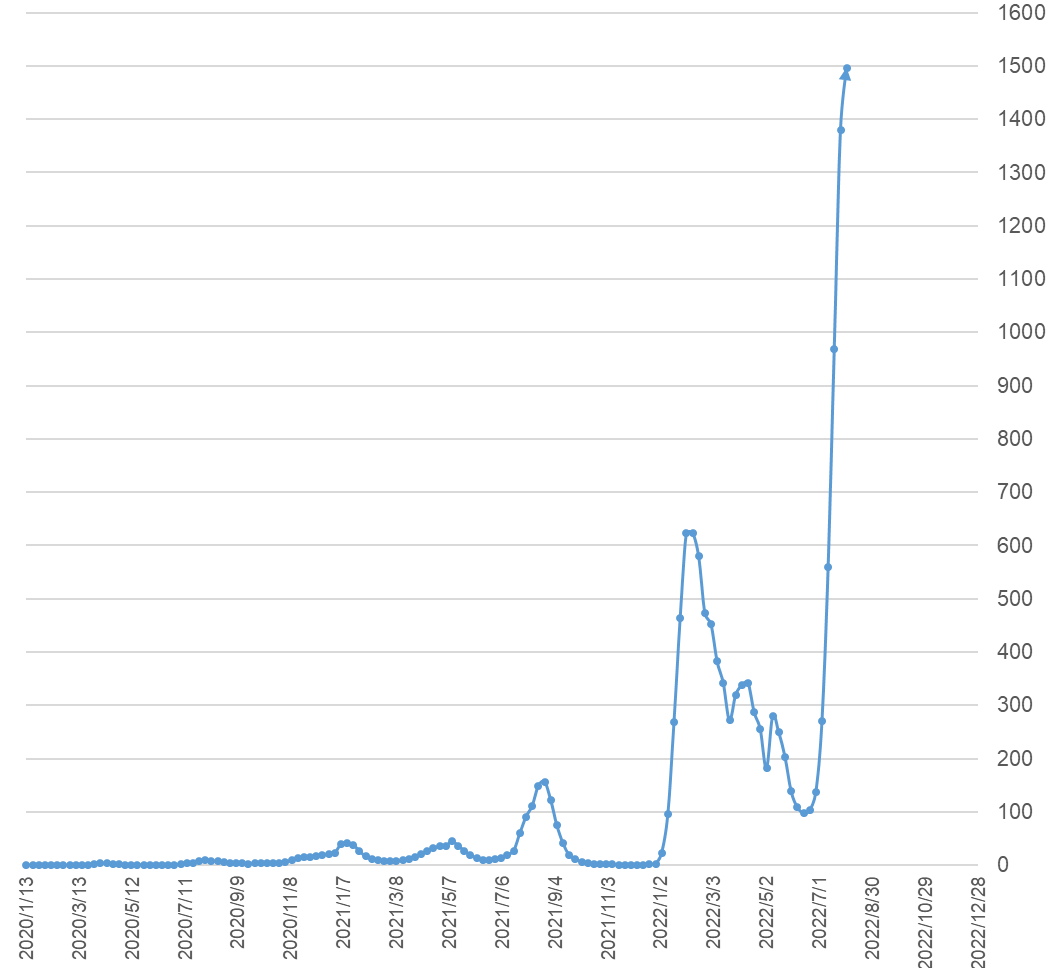
週別陽性者数の推移（単位：千人）

 

報道によると第七波ということですが、図１では最初の方の波がつぶれてしまっていて判別できませんので、縦軸を対数に変更してみます。

図２

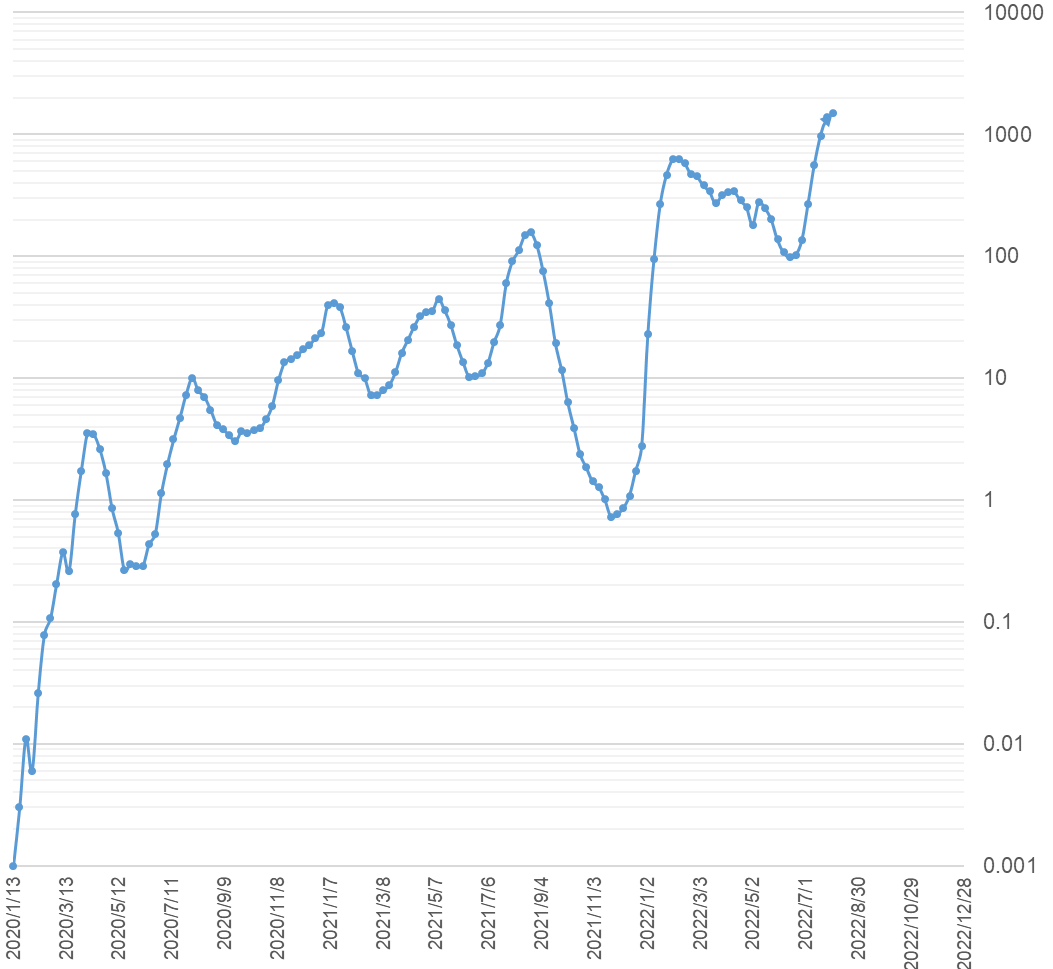
週別陽性者数の推移（対数軸、単位千人）

 

これで前半の波もはっきり読み取ることができます。確かに、現在は七回目の波のピークにあるのがわかります。また過去七回のピークが右肩上がりの直線上に並んでいるのもわかります。陽性者数が一人であった2020年1月13日の週を週番号１とすると、先週は134番にあたりますが、陽性者数がピークを打った週を拾っていくと以下のようになります。

表１

週番号	陽性者数がピークの週	陽性者数	前のピークからの経過週数
13	2020年4月6日の週	3,554
30	2020年8月3日の週	10,094	17週
53	2021年1月11日の週	41,521	23週
70	2021年5月10日の週	44,961	17週
85	2021年8月23日の週	156,931	15週
109	2022年2月7日の週	624.240	24週
134	2022年8月1日の週	1,496,968	25週
			平均20週

 

厚生労働省のHPから集計（2022年8月7日現在）

 

ほぼ、20週に一度の間隔でピークが訪れています。表１をグラフにすると図３になります。確かに、データはほぼ一直線に並んでいます。

 

図３

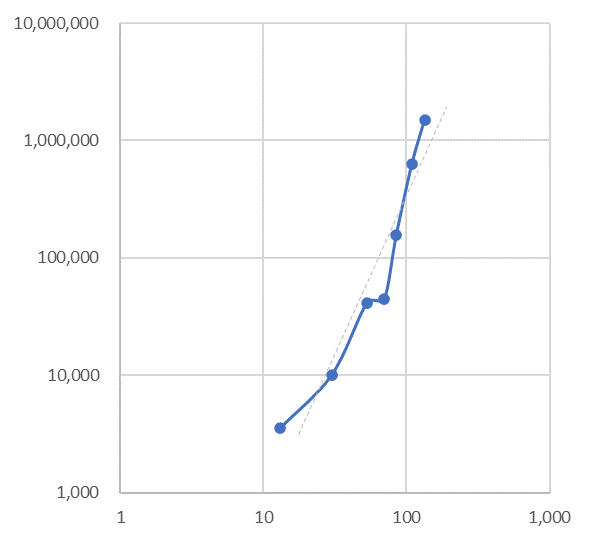
横軸はピークに達した週番号、縦軸はその週の陽性者数（いずれも対数）

 

次に、陽性者数を10万人、20万人、30万人・・・100万人・・・と、10万人間隔で区切って、その間隔に当てはまる陽性者を出した週の数を集計します。それを図３と同じ要領で、横軸を陽性者数の対数、縦軸を週数の対数にしてグラフにすると、

図４

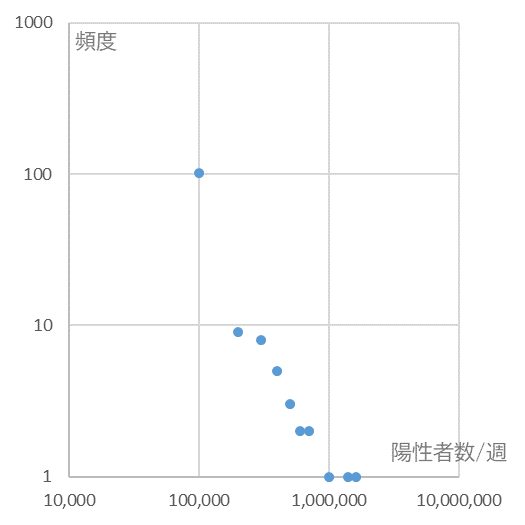
横軸は週別陽性者数、縦軸はその出現頻度（いずれも対数）

 

となり、興味深いことに、こちらの方もデータがほぼ一直線に並びます。毎日報道される感染者数はランダムに増減を繰り返しているようにしか思えませんが、実はそこには綺麗な法則があるようです。ちなみに図４をよくみると、134週の内、陽性者数が10万人以下であった週が100週もあったことがわかります（左上に離れてポツンとあるデータ）。ではその100週の中身はどうなっているのでしょう？区切りを5千人にします。すると、

図５

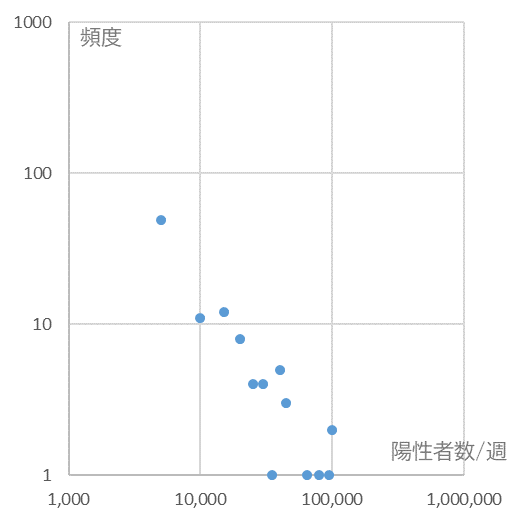
陽性者が10万人以下であった週の数とその出現頻度（いずれも対数軸）

 

これまた、データはほぼ一直線に並んでいるではありませんか！

実はこの法則は、地震の発生頻度と規模にもはっきりと表れます。法則の名前もついていて、「グーテンベルグ・リヒター則」といいます。グーテンベルグはドイツ人、リヒターはアメリカ人で、いずれも地震学者です。図６をご覧ください。

図６

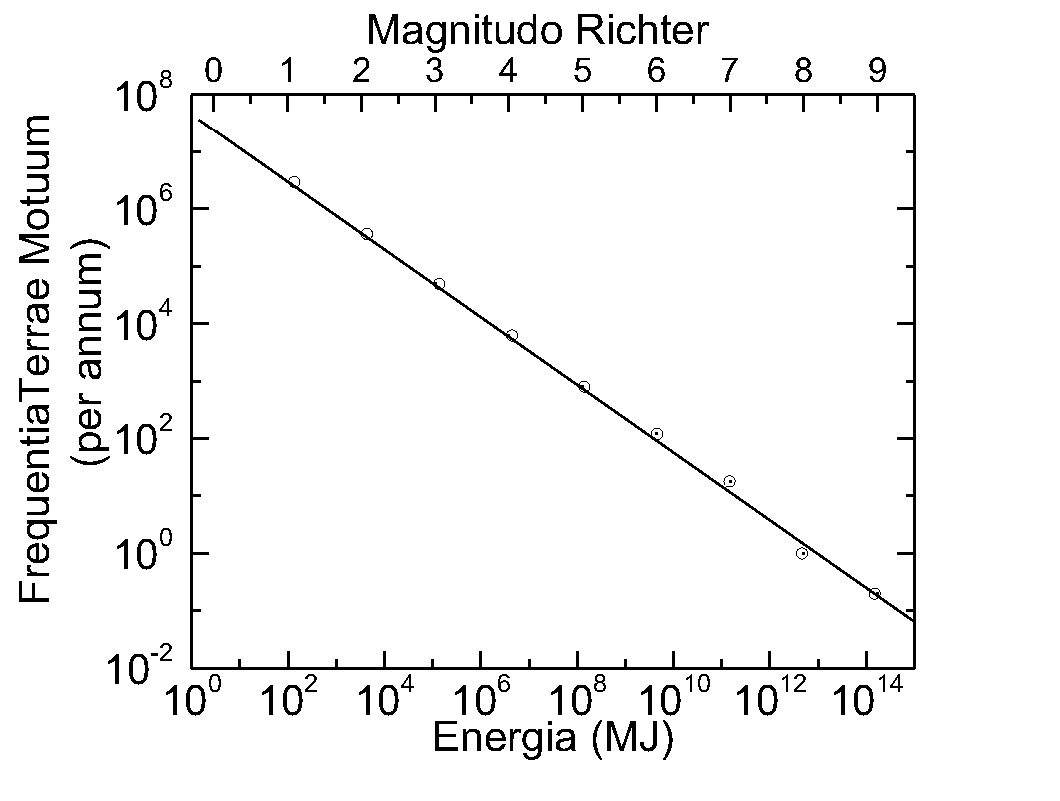
GR則 – 地震の発生頻度（縦軸）と規模（規模）Wikipedia

 

これだけ見事に一直線に並ぶならこの法則は数式に表せそうです。

週別陽性者を $x$、その出現頻度を $y$ として、その関係がべき乗則に従うのであれば、

$$y=ax^b\tag{0}$$

で、表せるはずです。

パラメーターの $a$ と $b$ の組み合わせをいろいろ試して、実際のデータにフィットする直線を探してみましょう。

図６

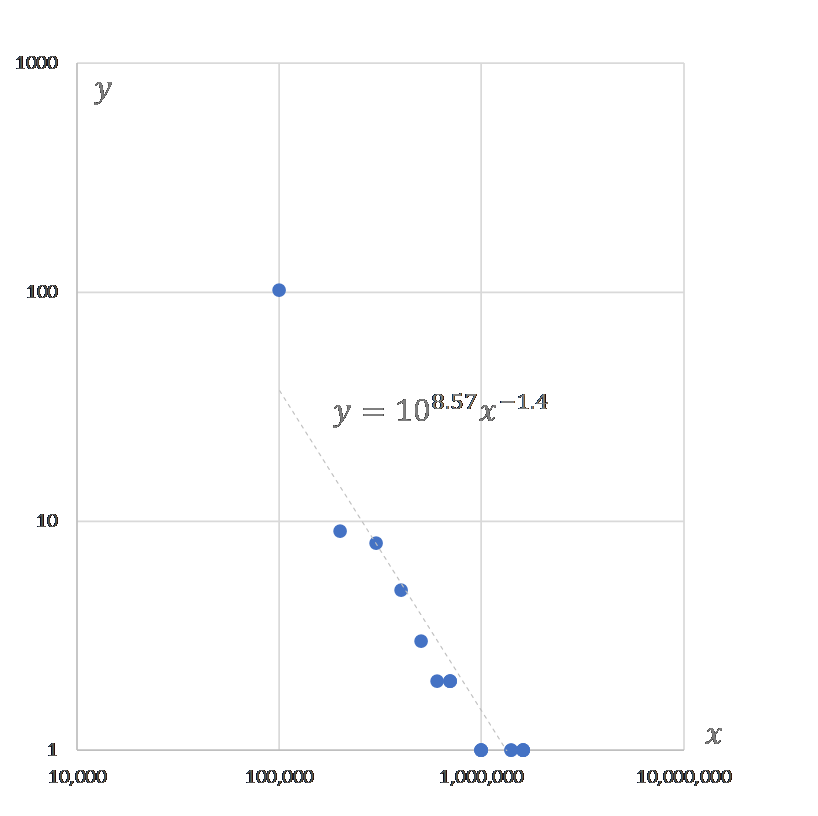
週別陽性者数 $x$とその出現頻度 $y$

$$y=10^{8.57}x^{-1.4}\tag{1}$$

図７

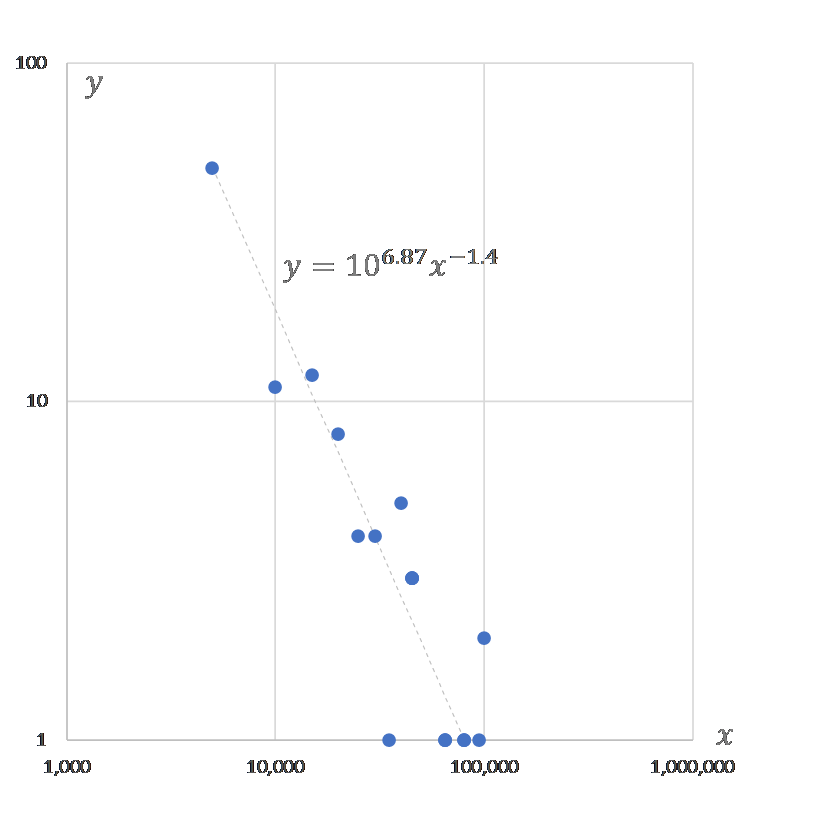
週別陽性者数（10万人以下）$x$ とその出現頻度 $y$

$$y=10^{6.87}x^{-1.4}\tag{2}$$

これで一応、数式化はできましたが、これらは陽性者数とその出現頻度の関係を表しているだけで、陽性者数の増減予測はできません。しかしながら、現在起こっている事象がどの程度珍しいのか、ありふれているのか、の判断はできます。冒頭に述べたように先週の陽性者数は約1.5百万人（一日平均21万人）ですが、これがたとえば五万人（一日平均7千人）くらいまで減ったとしても、式 $(2)$ より $x=50000$ のとき $y=2$ ですので、過去134週ある中でわずか二回くらいしか起きない珍しい事象である、ということがわかります。$x=5000$ のとき $y=49$ ですから、一日平均7百人くらいになって、ようやく「ありふれた」レベルに到達する、ということがわかります。

おわり

 

記事一覧へ戻る