2021年3月14日付のブログ「ドラゴン・キング理論で予測した「急落」は起こったか?」でブリヂストン株の事例をご紹介しましたが、本日は三菱UFJフィナンシャルグループ(以後、MUFG)で予測を試みます。
まずはMUFGの株価(終値)の推移を確認しましょう。
図1
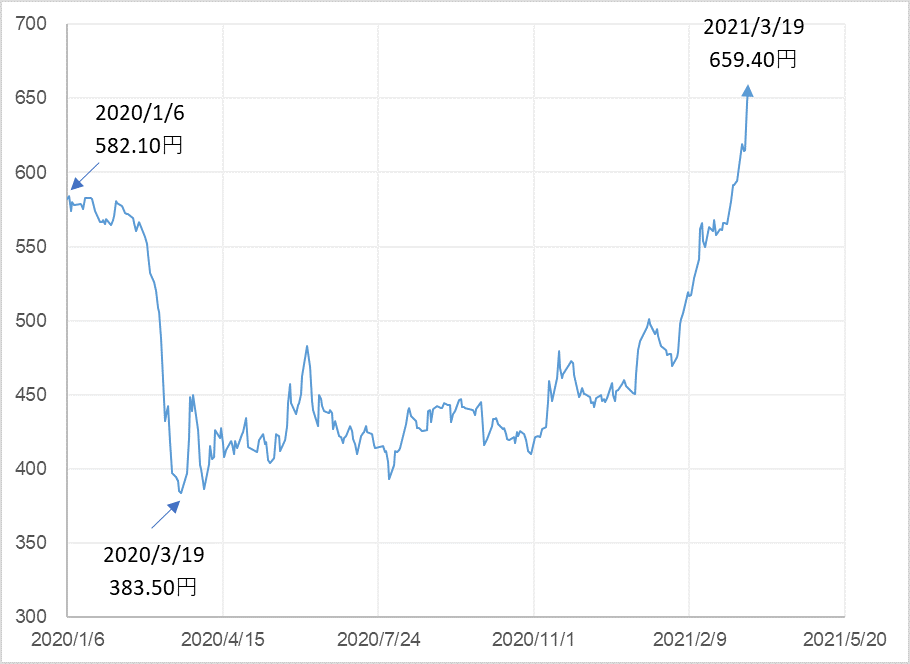
MUFGの株価(終値)の2020年1月6日~2021年3月19日の推移
COVID19ショックで2020年3月19日の底値に到達。1月6日の初値 582.10 円に対して34%下落しました。その後しばらく低迷していましたが、11月に入ると上昇に転じ、2021年の2月に入ると急回復がはじまり、3月19日(金)の時点でコロナショック前の水準をも超えて、659.40 円に達しています。
さて、ここからこれまでの動きと今後の動きを数理的に解析します。マクロとミクロの両面でチェックします。事象がバブル的な成長をしているかどうかは、事象が対数周期曲線に乗っているかどうかで判断できる、というのがドラゴン・キング理論でした。対数周期曲線とは事象の急激な上昇にゆらぎ(波打ち)が加わったもので、そのゆらぎの間隔がバブルの崩壊に向けて徐々に短くなるという特長があります。数式で表すと、
事象の急激な上昇 → べき乗 (Power Law) 曲線:
$$F_{pow}(t)=A+B(t_{c}-t)^m \tag{1}$$
事象のゆらぎ(波打ち) → 対数周期 (Log Period):
$$F_{lp}(t)=1+C\cos(ω\log((t_{c}-t)/T)) \tag{2}$$
(1)と(2)の掛け合わせ → 対数周期曲線:
$$F_{lp}(t)=A+B(t_{c}-t)^m[1+C\cos(ω\log((t_{c}-t)/T))] \tag{3}$$
となります。図1のチャートの2021年1月以降の動きに式 (3)をフィッテイングします。
図2
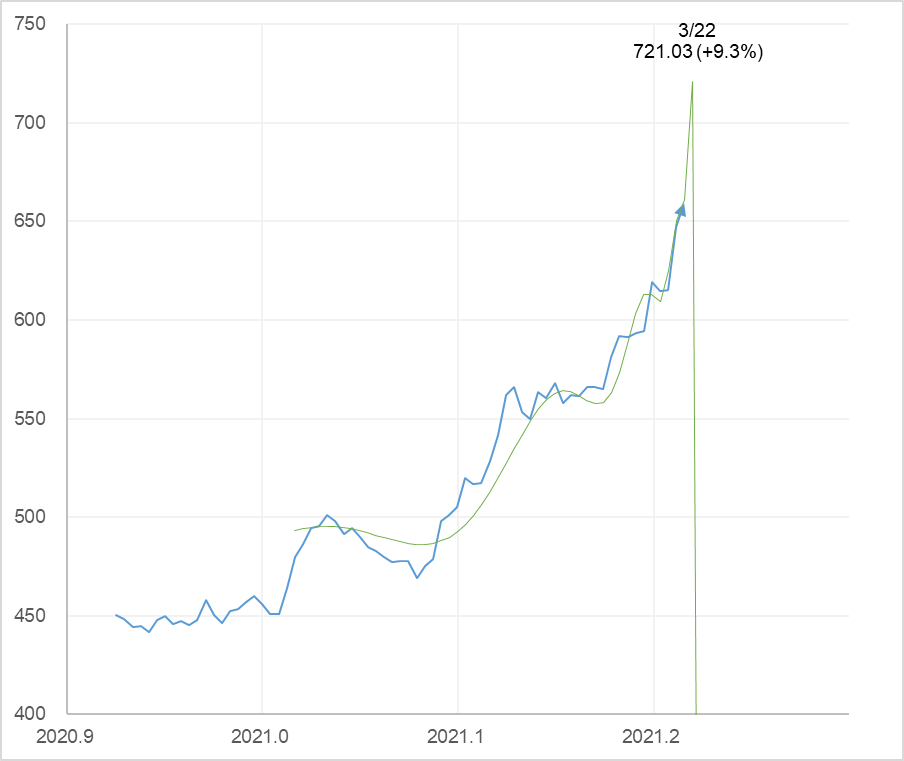
MUFGの終値と対数周期曲線。A=750, B=-450, m=0.3, C=0.08, T=1.55, tc=2,021.22(2020年3月22日)
頂点に記載した 3/22, 721.03 (+9.3%) は計算に使ったクリティカル・タイム (tc ) が2,021.22、つまり3月22日(月)であり、その計算結果が 721.03 円であることを示しています。+9.3% は、3月19日(金)の終値 659.40 円との値差です。ちなみに、tc を3月31日(水)にずらしてフィッテイングしたものが図3で、その場合の値差は +23.8%になります。いずれにしても対数周期曲線に乗るとその最終局面で上昇角度が急に立ち上がり、その後急落するという特長があります。
図3

MUFGの(終値)と対数周期曲線。A=900, B=-680, m=0.3, C=0.06, T=1.5, tc=2,021.25(2020年3月31日)。株価はより高い位置まで駆け登り急落のマグニチュードが蓄積する。
次はミクロ・チェックです。2021年1月以降の株価の推移を確率微分方程式から導かれる σ 曲線と対数周期曲線からゆらぎを取り除いたべき乗曲線のふたつを使います。
株価は絶えず指数関数的増加をしようとしている中で上下にゆらぎます。その瞬間瞬間の変化は以下の微分方程式で表せます。
$$\frac{dx}{dt}=rx+vx\frac{dB(t)}{dt} \tag{4}$$
$x$ が株価、$r$ は成長係数、$v$ はゆらぎ係数、$B(t)$ は日々のランダムな上下動です。この方程式を解くと未来の株価を予測できる式が得られます。それが、
$$x=x_{0}\ e^{(r-\frac{v^2}{2})t+vB(t)} \tag{5}$$
です。この(5)式によって任意の初期値 $x_{0}$ から時間 $t$ が経過したときの株価を求めることができます。ここで、もしブラウン項の $vB(t)$ がなければ式 (6) となります。株価 $x$ が向かう基本的方向を示しており、実際の株価 $x$ はこの式 (6) を中心として上下にゆらぎます。この中心線のことを $µ$ 線と呼びます。
$$x=x_{0}\ e^{(r-\frac{v^2}{2})} \tag{6}$$
$µ$ 線からのゆらぎの度合いは式 $(7)$ で表せ、これが $σ$ 曲線です。
$$x=x_{0}\ e^{(r-\frac{v^2}{2}+v□\sqrt{t})} \tag{7}$$
□の中に入る係数は、株価が上昇しているときはプラス、下降しているときはマイナスです。図2に $σ$ 曲線を書き込んだものが図4です。通常、どの株価も上に凸の上昇 $σ$ 曲線と、下に凸の下降 $σ$ 曲線が交互に現れます。それがちょうど N 字のように見えるのでそれを株価の N 字成長と呼びます。しかしながら、図4をよくみると3/5以降の動きは上に凸の $σ$ 曲線では近似できません。下に凸の上昇曲線である「べき乗曲線」が必要です。事象がべき乗曲線に乗るといずれ相転移がやってきます。
図4
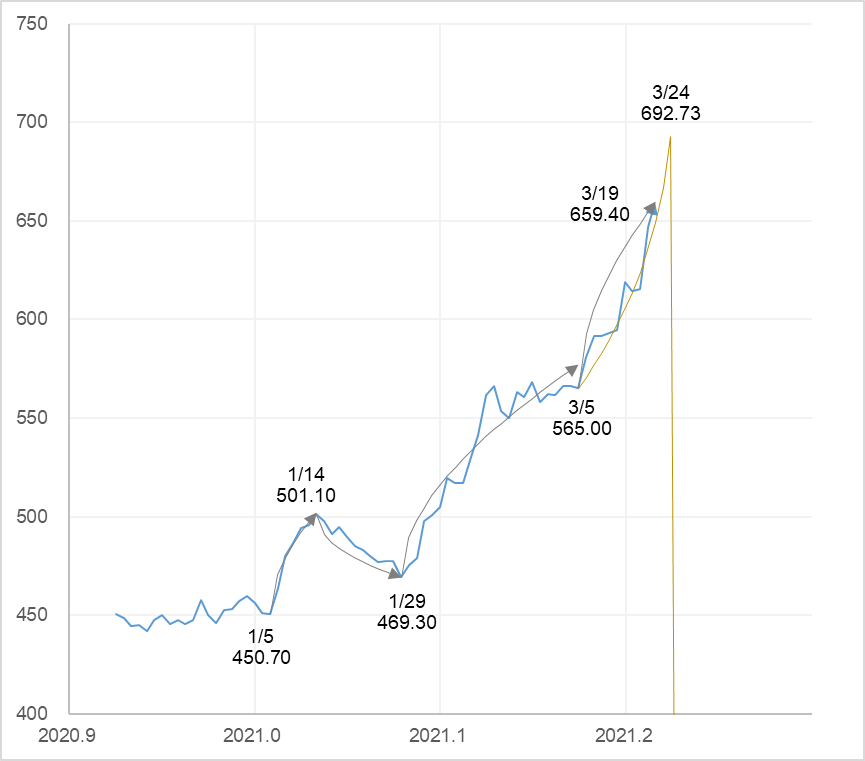
MUFG終値にフィッティングしたσ曲線とべき乗曲線。σ曲線に使用した係数は、r=4.4×10-4, v=0.016, 初期値 x0 =450.70 (1/5), 501.10 (1/14), 469.30 (1/29), 565.00 (3/5)。式(7)の□に入れたσ係数は、+2.7(1/5), -1.3 (1/14), +2.6 (1/29), +3.0 (3/5)。3/5~3/19のべき乗曲線に使用した係数は、A=850, B=-670, m=0.3, C=0.1, T=1.55, tc=2,021.232(2020年3月25日)。
以上より、マクロ的にもミクロ的にもMUFG株は今月中(2021年3月22日以降)に急落ポイントに到達する可能性が高いと予測されます。明日以降の株価の動きに注目しましょう!
以上