S&P500の対前日変化率の分析と簡単な確率的未来予測
はじめに
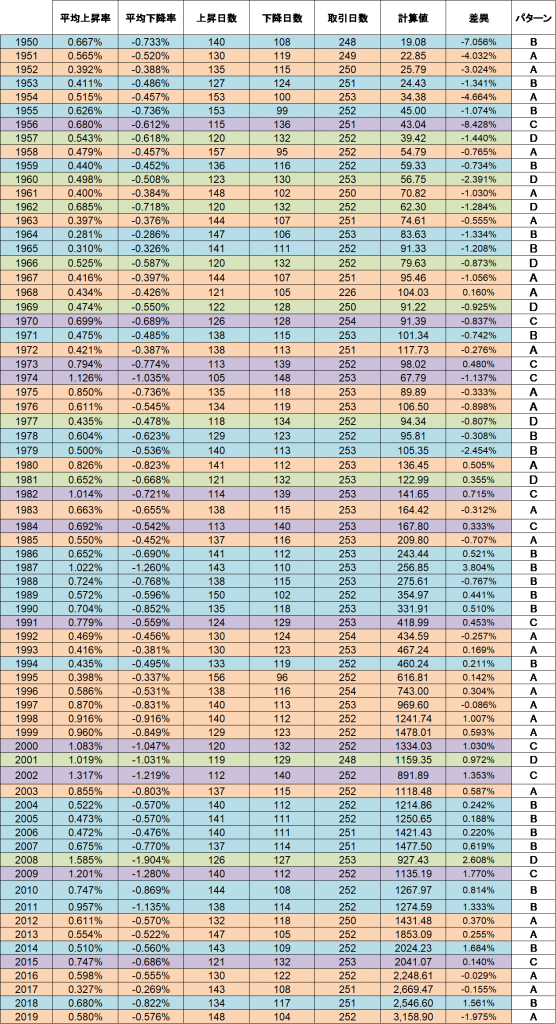
S&P500(米国株価指数)1950 年 1 月 3 日の終値 16.66 米ドルからさまざまな推移を辿っ て 70 年 4 ヵ月後の 2020 年 4 月 17 日現在、2,799.55 米ドルをつけている。取引日数にし ておよそ 1 万 7 千日。翌日の指数は上がるか、下がるかの二通りしかなく、あとはその上 げ幅と下げ幅(まとめて変化率と呼ぶ)がどの程度かという二つの要素、合わせえ「四つの 要素の組み合わせ」が 1.7 万回繰り返されて今日の指数に至っている。まず変化率について 解析を行ったうえで、「四つの組み合わせ」に関するパターン分析を行い、そこから一年後 の指数(以下、単純に株価と呼ぶ)を確率的に予測する簡単な方法を示す。
- 上昇・下降日数と変化率の解析
過去 70 年間、前日に対して S&P500 の上昇率と下降率の平均値、上昇した日数の合計と下 降した日数の合計を集計したものが表0である。17,680 日あった取引日の中で前日より指 数が高かった日は計 9,388 日で、低かった日よりも 1,096 日多い。これは年間平均で僅か 16 日弱という差異である。一方、興味深いことに、対前日の変化率の平均値は逆に下 降率が上昇率を 0.0237%上回っており、微妙なバランスが保たれていることがわかる。
表0
| 頻度 | 変化率 | |
| 上昇 | 9,388回 | 6.503×10-3 |
| 下降 | 8,292回 | -6.740×10-3 |
| 差異 | 1,096回 | -2.370×10-3 |
本日の株価 $x_{n}$ は前日の株価 $x_{n-1}$ が何パーセントかの変化をして形成される。その変化率を $w_{n}$ とすると、本日の株価 $x_{n}$ は、
$${x_{n}=x_{n-1}(1+w_{n}) \tag{1}}$$
である。同様に、前日の株価 $x_{n-1}$ は一昨日の株価 $x_{n-2}$ と変化率 $w_{n-1}$ から構成されているので、
$${x_{n-1}=x_{n-2}(1+w_{n-1}) \tag{2}}$$
である。$(2)$ を $(1)$ に代入すると、
$${x_{n}=x_{n-2}(1+w_{n-1})(1+w_{n}) \tag{3}}$$
これを繰り返していくと初期値 $x_{0}$ から $n$ 日後の株価 $x_{n}$ を得る式になる。対前日比がプラス のときの変化率を $a_{n}$、マイナスのときの変化率を $b_{n}$ とすると、$a_{n}$ と $b_{n}$ はランダムに表れる ので、$n$ 日後の株価は、たとえば
$${x_{n}=x_{0}(1+a_{1})(1−b_{1})(1+a_{2})(1+a_{3})(1−b_{2})(1−b_{3}) \cdots}\tag{4}$$
$(𝑎, 𝑏>0)$
のように書ける。変化率がプラスであった日の合計を $p$ 、マイナスであった日の合計を $q$ だとすると、$(4)$ は、
$${x_{n}=x_{0}((1+a_{1})(1+a_{2})(1+a_{3})\cdots(1+a_{p}))((1−b_{1})(1−b_{2})(1−b_{3})\cdots(1-b_{q})) \tag{5}}$$
と書き換えることができる。変化率の掛け算が長々と続くので、単純に変化率の平均値に置 き換えてみよう。そうすると $(5)$ 式は、
$${x_{n}=x_{0}\ \left(1+\frac{a_{1}+a_{2}+a_{3}+\cdots+a_{p}}{p}\right)^p\ \left(1-\frac{b_{1}+b_{2}+b_{3}+\cdots+b_{q}}{q}\right)^q \tag{6}}$$
すなわち、
$${x_{n}=x_{0}(1+a_{\bar{p}})^p\ (1−b_{\bar{q}})^q\tag{7}}$$
$(𝑝+𝑞=𝑛,\ 𝑎,𝑏>0)$
となり、すっきりした形になる。$(7)$式は正負の変化率の平均値 $a_{\bar{p}}$ と $b_{\bar{q}}$ 、それぞれの日数 $p$ と $q$ が分かれば $n$ 日後の株価が計算できるということを示している。これを S&P500 に適用してみると初期値 $x_{0}=16.66$、正負の変化率と発生日数は表1のとおりなので、それぞれの値を$(7)$式に代 入すると、
$${x_{16780}=16.66\ (1+6.503×10^{-3})^{9388}\ (1−6.740×10^{-3})^{8292}=1974.86}$$
となる。17,680 日後の実際の株価は 2,799.55 であるので 800 ドル以上低い値であり誤差が大き過ぎる。では この簡易的な計算方法に使い道はないのだろうか。ここで期間を 70 年から 1 年に短縮してみよう。
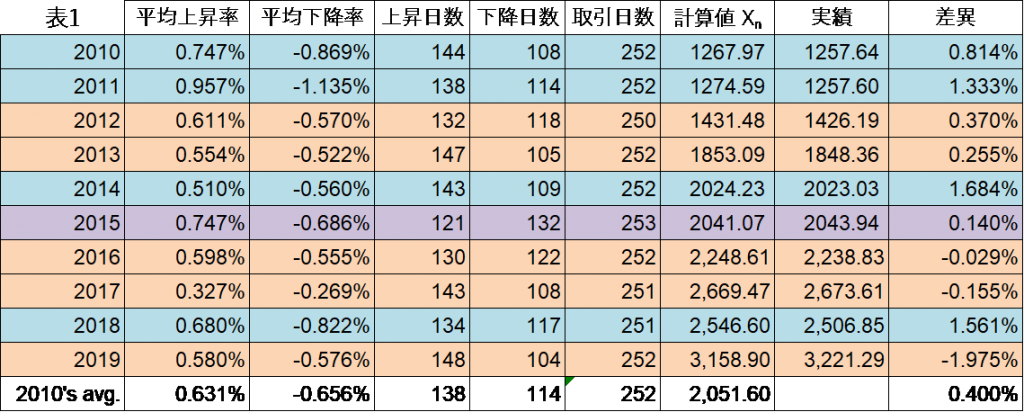
表 1 が直近の 10 年間の実績と計算結果の比較である。右端の差異というのが計算 式 $(7)$ で得られた値と実際の値(各年度末の終値)の差である。平均すると 0.4% の差異にと どまっており、この程度であれば予測に使えそうである。
- 上昇・下降日数と変化率のパターン分析と近未来予測
繰り返しになるが、株価は上昇・下降日数と変化率の組み合わせにより決定されるわけだから、組み合 わせとして以下の四つのが考えられる(表 2)。組み合わせの A は上昇した日数の方が下降した日数よりも多く、上昇率も下降率より高かった年。B は上昇日数の方が下降日数よりも多かったが、上昇率が下降率より低かった年。C は上昇日数が下降日数よりも少なかった が、上昇率が下降率よりも高かった年。D は上昇日数と上昇率が下降日数と下降率よりも低 かった年である。発生確率が最も高いのがパターン A で 38.6%、二番目に高いのがパター ン B で 34.3%、以下、パターン C の 14.3%、D の 12.9%と続く。表 1 の色分けは表 2 に対 応している。

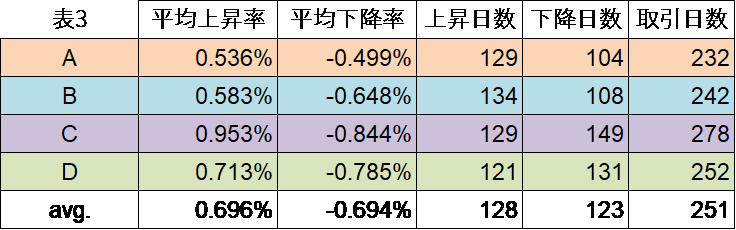
では次に、それぞれのパターンにおける実際の上昇・下降日数、変化率をみてみよう(表 3)。
パターン A は表 2 から過去 27 回出現しているが、表 3 はさらにパターン A の平均上昇日数 は 129 日、同下降日数は 104 日、平均上昇率は 0.536%、同下降率は 0.499% だったことを示 している。
次に知りたいことは、それぞれのパターンがどのくらいの確率で出現しているか、さらには どのパターンのあとにどのパターンが出現しやすいか、という点である。パターンは A から D の四通りあるので、出現パターンの順番は全部で 16 通りある。そしてその 16 通りが実際どの程度の確率で発生したかを示したものが表 4 である。

表 5 は翌年出現するパターンの確率を示したものである。たとえば 2020 年は パターン A であったので翌年もパターン A である確率は 38.5% ある一方で、パターン D に なる可能性も 15.4% あるということを示している。過去データが合計 70 しかないのでこの 確率はかなりおおざっぱの域は出ないが、目安にはなろう。

さて、ここまでくれば計算式 $(7)$ を使って、翌年の株価を確率的に予測することができる。初 期値は昨年度の終値、パターン別の上昇・下降日数、変化率の値は表 3、次に現れるであろ うパターンの確率は表 5 をみればわかる。表 6 と図 1 が 2017 年の終値から 2018 年の終値 を予測したとき、表 7 と図 2 が 2018 年から 2019 年を予測したときの予測値と実績である。
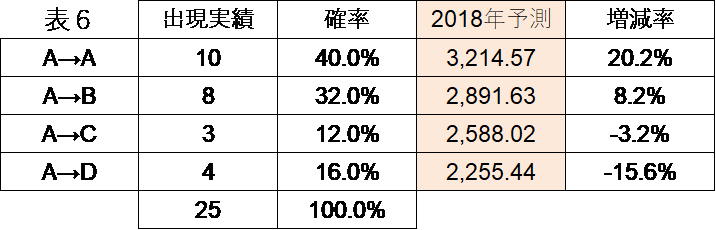

2017 年の終値 2,673.61 に対して、2018 年の終値は 2,506.85 だった。
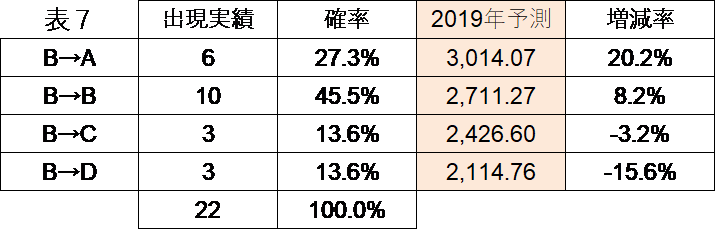

2018 年の終値 2,506.85 に対して 2019 年の終値は 3,221.29 だった。
それでは最後に今年度(2020 年)の株価を予想してみよう。2019 年の終値 3,221.29 ドルに 対して、2020 年の終値の予測幅は 2,771 ドルから 3,822 ドルである。
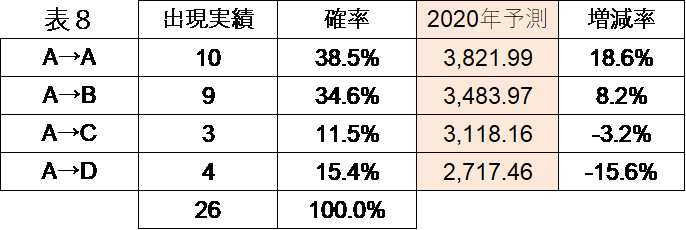
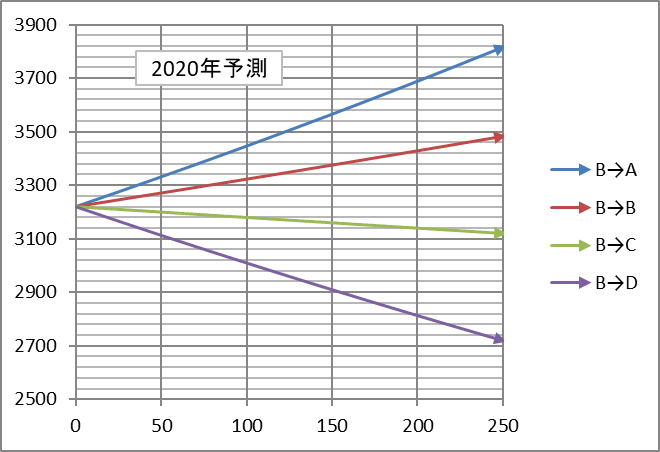
2019 年の終値 3221.29 に対して、2020 年の終値は?
- 結論
株価が形成される単純な四つの要素に注目し、予測値を算出する計算式を導き、その計算値 と実績値を比較することによって一年くらいのスパンであれば計算式から近似値が得られ ることを確認した。さらに、過去 70 年間において四つの要素がどのように組み合わさり変 移したかをパターン分析することによって、次年度の株価が到達するであろう領域を確率 的に予測できることを示した。非常に単純な手法であるが、具体的な予測株価を計算できだけでなくその出現確率も分かるところがこの手法の特長である。