2021年2月15日付のブログ「ドラゴン・キング理論(後編)」で予測したブリヂストン株の急落は果たして起こったか?をここで検証します。
2月15日時点でそれまでの株価の動きに対数周期曲線をフィッティングしたところ、明日にでもドラゴン・キングが現れてもおかしくない状況でした(図1)。
図1
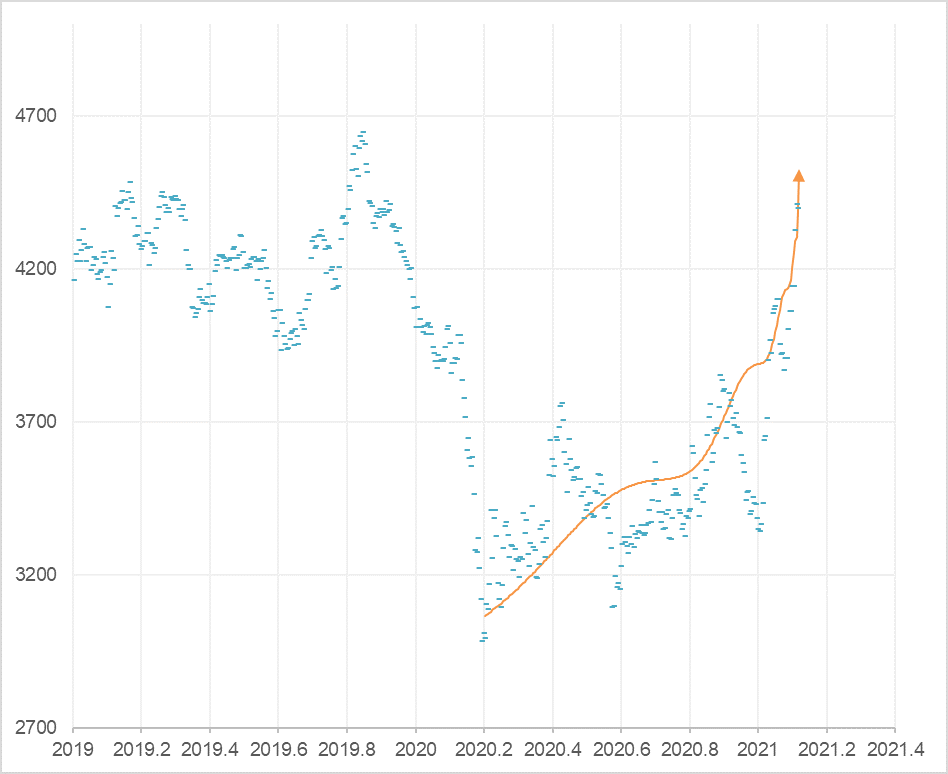
ブリヂストン株の終値推移。2021年2月15日に描いた対数周期曲線はクリティカル・ポイント(急落のはじまり=tc)が間近に迫っていることを告げていた。
対数周期曲線:A+B(tc-t)m[1+Ccos(ωlog(tc-t)/T)]
A= 5,000, B = -1,900, m=0.28, C = 0.06, ω = 7.7, T = 1.2, tc = 2021.12(2021/2/17)
<検証>
翌日の2021年2月16日の4,455円でピークに到達した後、翌々日の2月17日から急落がはじまり2月26日の4,161円まで、一気に6.6%下げました。
ソーネット教授が命名した「ドラゴン・キング」が登場すると10日以内に12~30%急落します(Why Stock Markets Crash, 2003, p63) 。一方、10%前後の下落であっても投資家にとって無視できない大きな動きですから何某かの名前を与えたいところです。ちなみにポケモン図鑑によるとドラゴン・キングと姿かたちがそっくりなのはリザードン(No.006)です。そして、リザードンに進化するのがリザード(No.005)ですので、今回はリザードの仕業ということにしておきましょう。


リザード(左)とリザードン(右)(ポケモン図鑑より)
図2
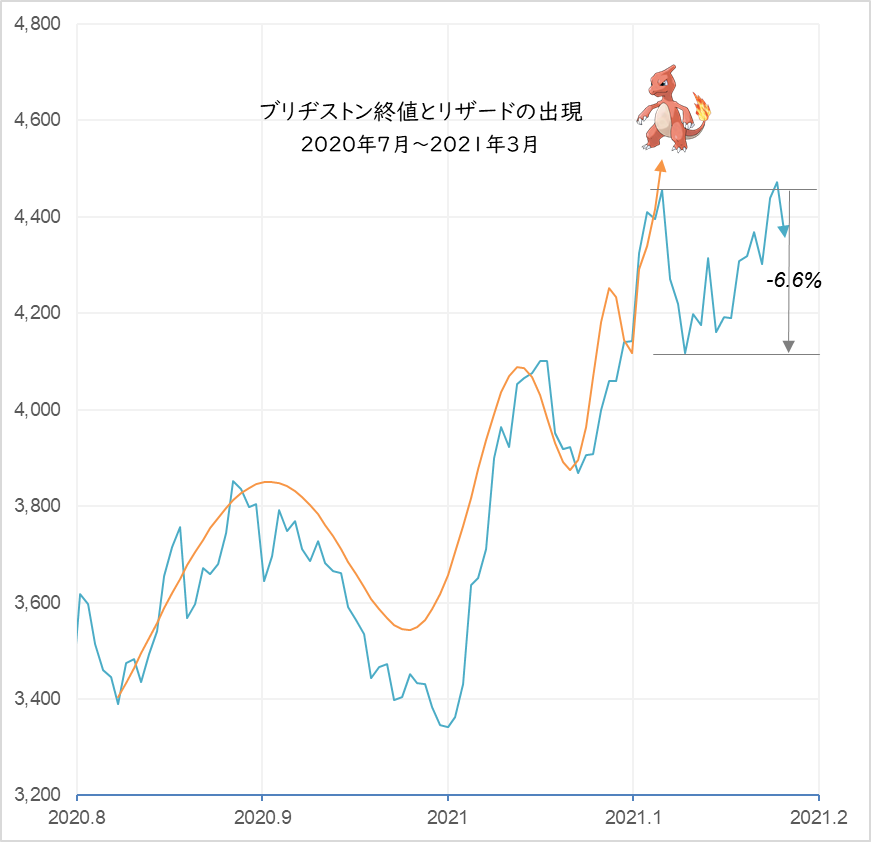
ブリヂストン終値の推移と新たに描いた対数周期曲線
A= 4,650, B = -1,800, m=0.35, C = 0.24, ω = 9.6, T = 1.55, tc = 2021.12(2021/2/17)
確率微分方程式から導かれる確率分布曲線(σ線)は、上昇局面においては上に膨らむ弓形線ですが、対数周期曲線は下に膨らむ弓形線です。図3の1月29日から2月16日の動きに注目してください。この間の動きをトレースできるのは上に膨らむσ線ではなく、下に膨らむ弓形線です。この下に膨らむ弓形線のことを以後、「べき乗曲線」と呼びます。べき乗曲線にゆらぎを与えると対数周期曲線になります。数式は以下のとおりです。
べき乗 (Power Law) 曲線:
$$F_{pow}(t)=A+B(t_{c}-t)^m \tag{1}$$
対数周期 (Log Period):
$$F_{lp}(t)=1+C\cos(ω\log((t_{c}-t)/T)) \tag{2}$$
対数周期曲線:
$$F_{lp}(t)=A+B(t_{c}-t)^m[1+C\cos(ω\log((t_{c}-t)/T))] \tag{3}$$
図3
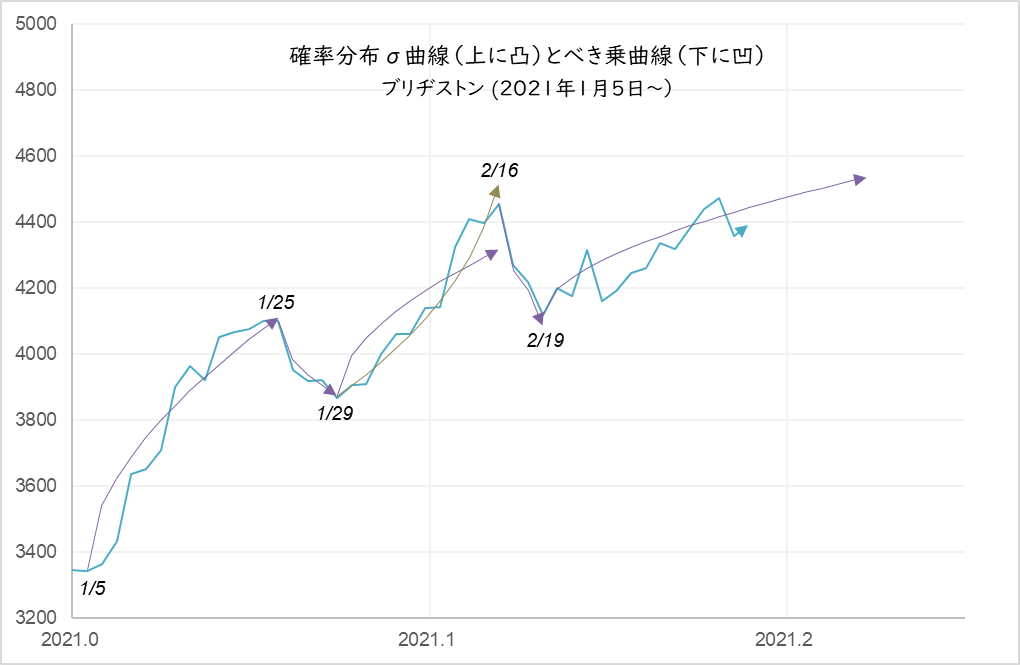
1月29日から2月16日まではべき乗曲線に沿っており、その結果として -6.6%の調整が入ったと捉えることができる。
べき乗曲線: A+B(tc-t)m(A=4,950, B=-3,100, tc=2021.123, m=0.35)
このように確率分布$σ$線とべき乗曲線のふたつで株価の動きを常時チェックしていると今後の株価をかなりの精度で予測できるだけでなく、急落の兆候をもある程度事前に掴める可能性がありそうです。
引き続き検証していきます。
以上
<追記>
リザード出現の新しい事例があります。2021年6月2日付のブログ「スモール・ドラゴンの出現予測と検証」をご覧ください。(2021年7月2日)