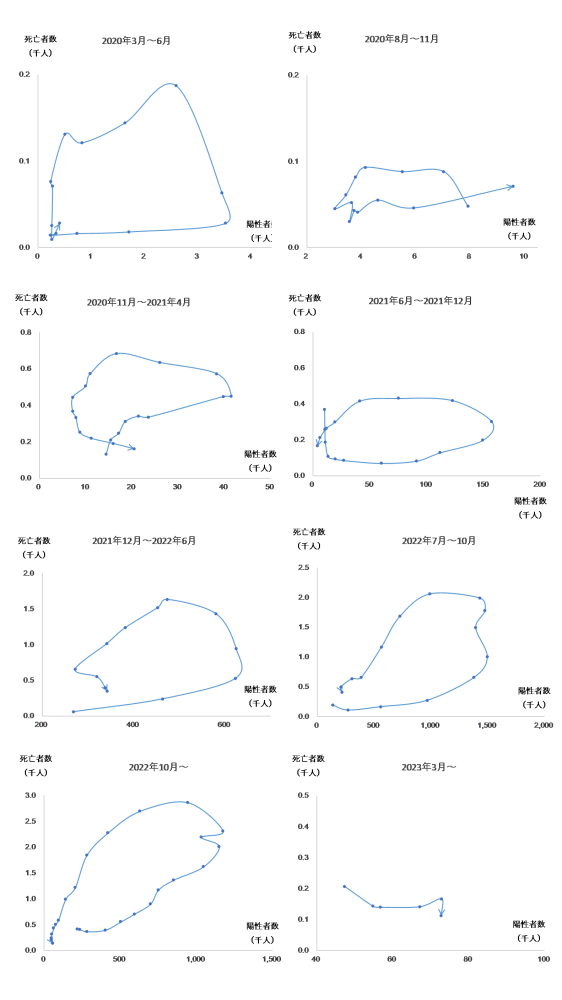
図1の青色のドットは厚生労働省のホームページで公表された新型コロナウィルス感染症の感染者数を週別に集計したものです。青色の実線は2023年5月までの各変異種の合成波です。同感染症の感染症法上の位置づけ変更に伴い、2023年5月7日分のデータが最終集計値となっています。
変異種の出現に関する数理的考察は、2021年8月18日付のブログ「新型コロナウィルス変異種の存在を説明する数理モデル – 逃げる抗原、追いかける抗体」をご覧ください。
図1
新型コロナ・ウィルスの感染者数(単位:千人)
破線が各変異種の感染者数、実線が合成波
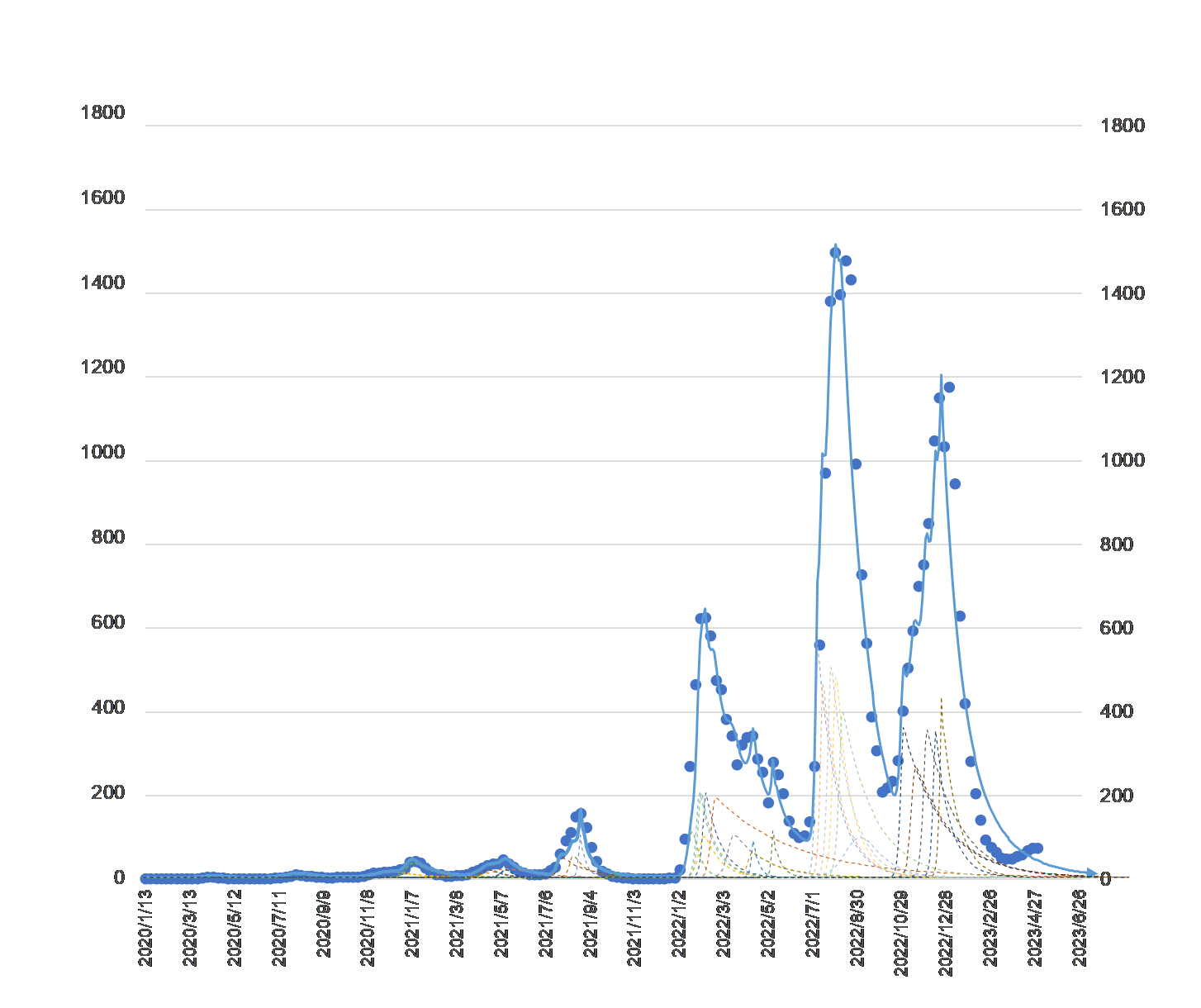
2023年5月7日現在
縦軸(単位:千人)を対数にすると、
図2
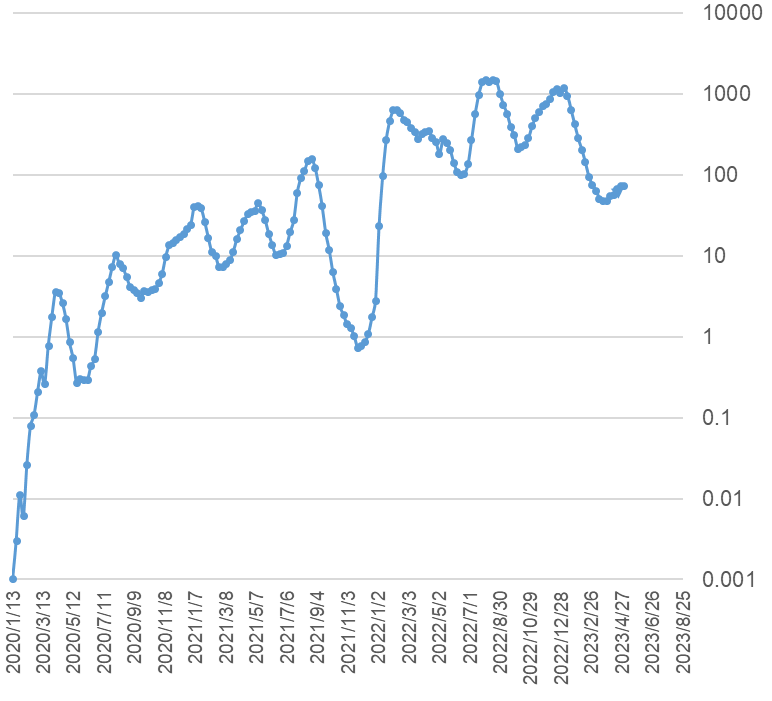
COVID-19 の週別陽性者数(対数軸、単位千人)
2023年5月7日現在
となり、感染者数が波打っている様子がよくわかります。波の山から次の山までの間隔を集計して平均するとおよそ20週です。
<収束予測を計算するための数理論>
感染する可能性のある人の数を $x$(以下、未感染者)、感染していて他人にうつす可能性のある人の数を $y$(以下、感染者)としたときに、それぞれの変化率は以下の微分方程式に従うとして予測しています。(注意:「未感染者」には、感染者との接触を避けている、感染しないようにしている、ひとは含まれません。詳しくは 2020年4月16日付ブログ「外出自粛は新型コロナ・ウィルス感染症の収束を速めるか?」と2020年11月22日付ブログ「新型コロナ・ウィルス感染者数が波打つ理由」をご覧ください。)
$$\frac{dx}{dt}=-bxy\tag{1}$$
$$\frac{dy}{dt}=bxy-cy\tag{2}$$
式 $(1)$ は未感染者が感染者と接触して減少すること、式 $(2)$ は、その結果感染者数が増加する一方で、治癒したり、亡くなったりして感染者ではなくなること、を表しています。係数の $b$ は「感染係数」、$c$ は「治癒係数」です。合成波(青色の実線)を構成する各波(破線)の係数は以下のとおりです。
表1
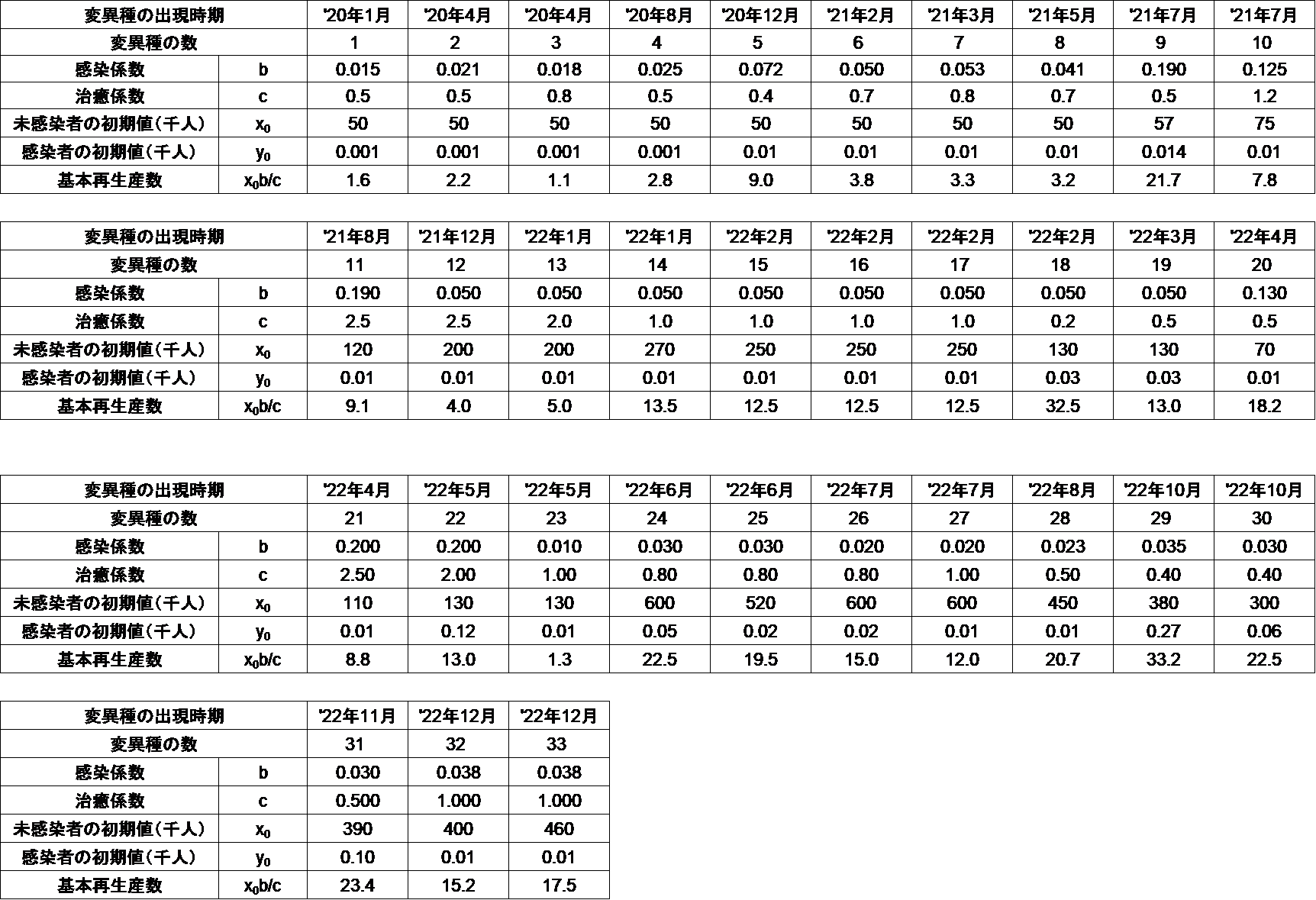
以下は、厚労省ホームページ、報道関連資料から2020年8月3日以降のデータを週別に集計しグラフ化したものです。ご参考まで。
図2
検査数と陽性者数の相関関係
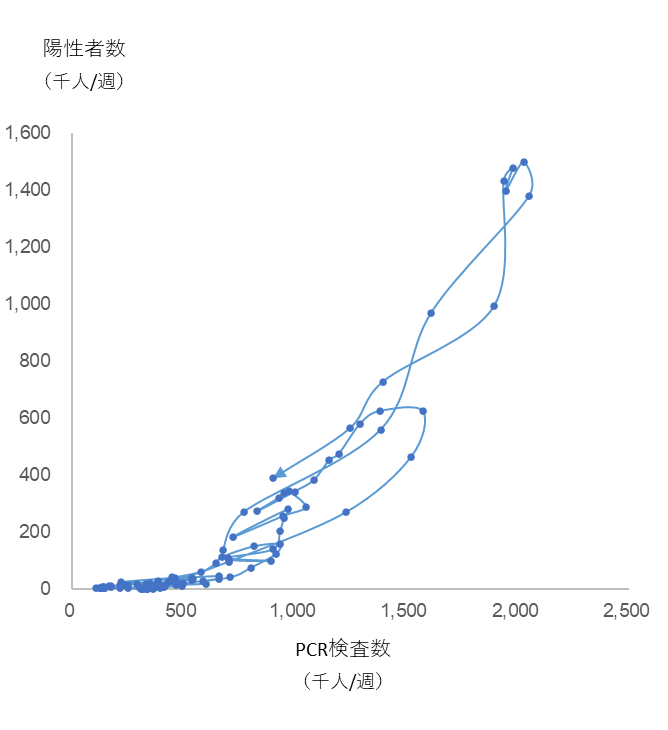
PCR検査数と陽性者数、ふたつのデータをエクセルの関数 =CORREL(陽性率の推移,死亡率の推移) に入れて計算すると、相関係数 r = +0.89が得られ、強い正の相関があることがわかります。(一般に相関係数 r が 0.7 ≦ r ≦ 1.0 にあると「強い正の相関」があるとされます。)「PCR検査をすればするほど陽性者が増える」ということを示しています。
2022年9月25日現在
(厚労省による検査数の公表は2022年9月26日で終了しています。)
図3
陽性率と陽性者死亡率の相関関係
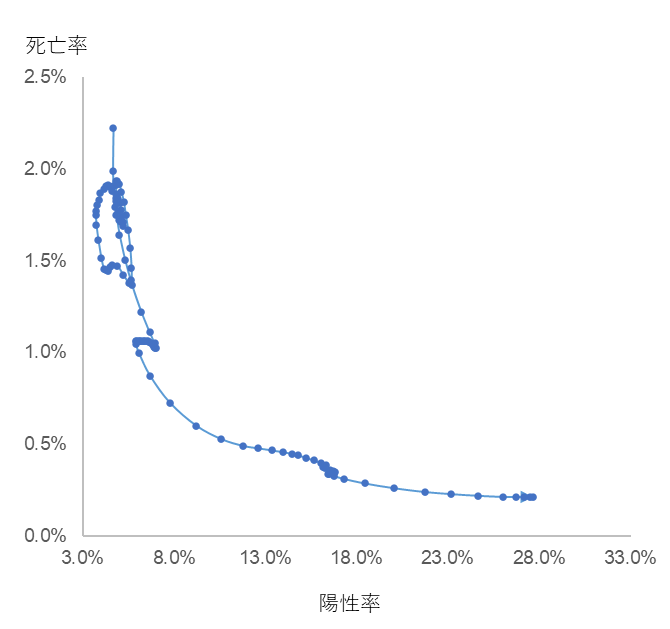
一方、PCR検査陽性率と陽性者死亡率の相関係数 r は -0.89 で強い負の相関があります。陽性率が上昇する一方で、死亡率は下降しており、重篤化リスクが減少していると推察されます。経済活動再開の数理的根拠といえるでしょう。
2022年9月25日現在
(厚労省による検査数の公表は2022年9月26日で終了しています。)
一方、死亡者数の日次推移をヒストグラムにすると、陽性者数同様、おおよそ八つの波が現われます。図4をご覧ください。正規分布は平均と標準偏差というふたつの変数でその形が決まりますが、それらを実際のデータに合うように調整すると、これまでの分布がうまく説明でき、今後の分布、つまり「収束時期」をおおよそ推察することができます。
図4
COVID-19 による死亡者数の日次推移と正規分布による合成近似
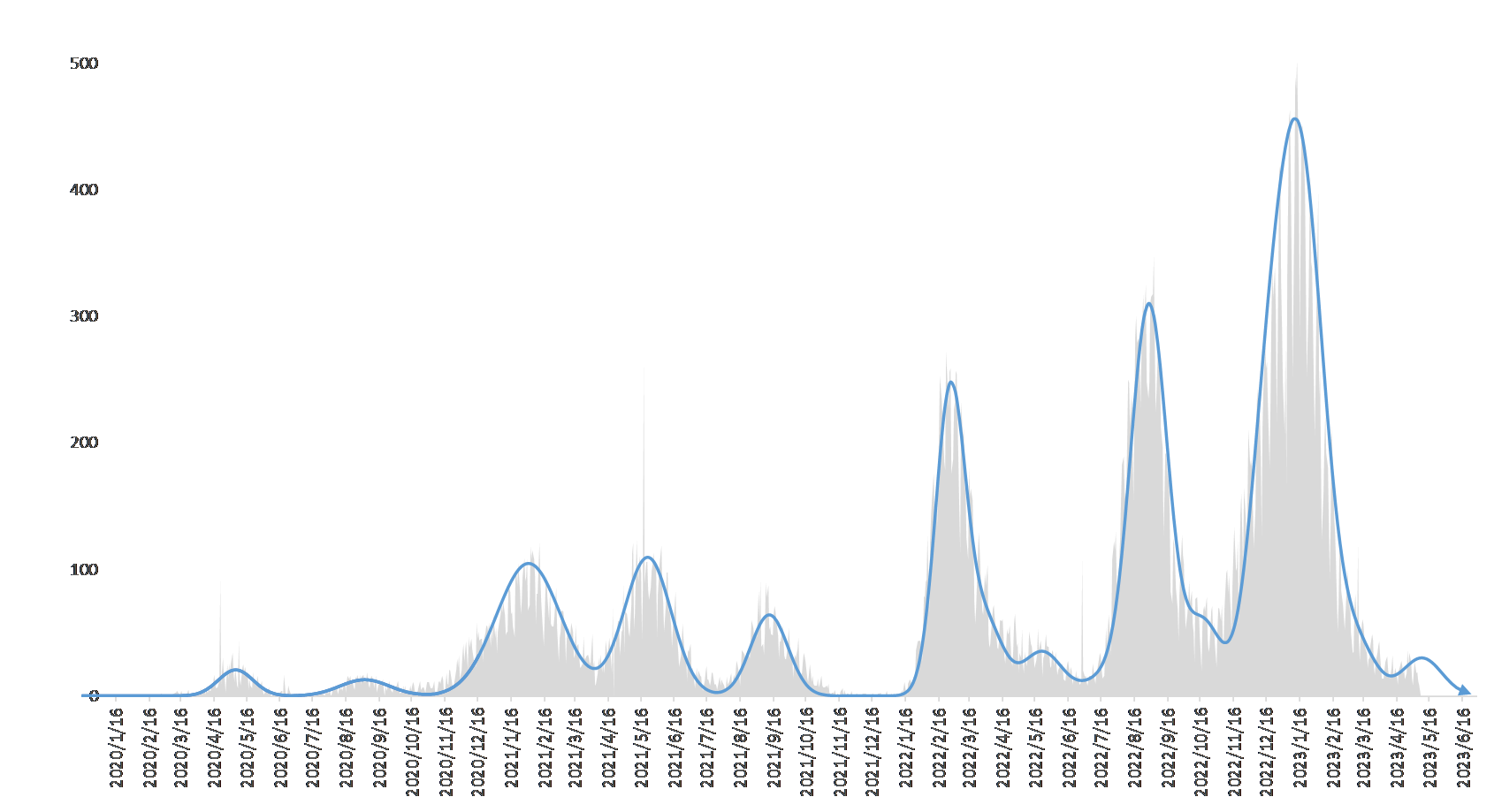
正規分布を合成することでもおおよその収束時期がわかります。
2023年5月7日現在
収束時期は陽性者数と死亡者数の回転関係によっても予測することができます。陽性者数を横軸に、死亡者数を縦軸に取ると左回りに平均十三週で一回転します。図5のとおり、回転は繰り返されているので、それが最後の収束かどうかまではわかりません。
図5
陽性者数と死亡者数は平均13週で左回りに一回転します。
2023年5月7日現在
いつまで感染が続くのかは、100年前に大流行したスペイン風邪の死者数(月別)の推移が参考になります。図6をご覧ください。流行期間は1918年から1921年の四年で、その間に五回のピークがあったことがわかります。
図6
COVID-19(グレー)と100年前に大流行したスペイン風邪(青)の月別死亡者数の比較
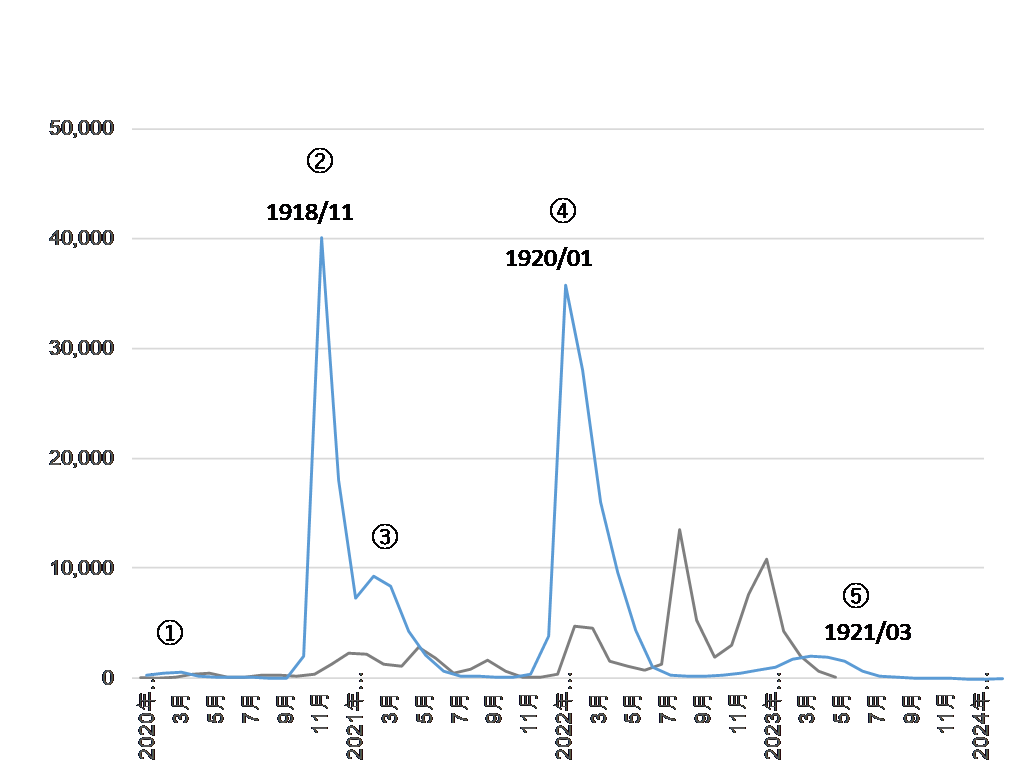
2023年5月7日現在
スペイン風邪のデータは東京都健康安全研究センターのHPより。
比較のため横軸と死亡者数(縦軸)のスケールを合わせています。
100年前のスペイン風邪の流行期間は1918~1021年の四年で、ピークが五回あったことがわかります。
東京都健康安全研究センター 年報56、2005 によると、スペイン風邪による感染者数は2,380万人、死亡者数39万人です。1920年当時の人口は5,600万人でしたから感染率は43%、死亡率は1.6%でした。一方、新型コロナウィルスの感染者数は2023年4月16日現在で、3,379万人、死亡者数は7.5万人です。日本の人口は現在1億2,500万人ですので感染率は26%、死亡率は0.22%です。インフルエンザの特長として「流行時期によりウイルスが変異することが往々にして観測される.スペインかぜ流行の際にも原因ウイルスが変異し,その結果として死亡率が大幅に増加したものと考えることができる.」と述べられており、さらには「今後のインフルエンザ対策を企画立案する際には,「再燃」について十分配慮していくとともに,インフルエンザウイルスの抗原性を経時的に観測していき,ウイルスの変異にすばやく対処することがぜひとも必要である.ウイルス変異を早期に検出できれば,新型インフルエンザの流行を未然に防ぐことも可能になるものと考える.」と、変異とその対応への重要性が指摘されています。
「変異種を早期発見して対処すべし」という主旨ですが、ワクチンの開発は後追いにならざるを得ず、変異種に対応するワクチン接種がはじまったころには次の変異種がすでに流行しているというのが現実です。実際のところ、新型コロナウィルスについても、三回、四回とワクチンを接種していても感染するケースがあることから、効果は限定的です。また、外出禁止などの強制的な封じ込めは経済活動を大きく阻害しますので、有効な対応策がないのが実情です。ウィルスは手強く、人類はこのようなパンデミックにこれから何度も遭遇することになるでしょう。
新型コロナウィルスで実際に観測されている変異株については国立感染症研究所が継続的に報告書2022年12月16日付の第23報 を出していますので表1と合わせてご覧ください。
おわり
記事一覧へ戻る