1年前の2020年5月30日付ブログで「何割のひとが新型コロナウィルスの抗体を獲得するか？」をアンダーソンとメイのモデルを使って予測しました。当時のPCR検査陽性者数は1万7千人、抗体保持者数は、そのころに米国で行われた抗体保有率検査を参考にして「陽性者と回復者の20倍、免疫損失率1%」と仮定して五年後の抗体保有者数を予測計算しました。その結果は54万人でした。

抗体保有率の調査は厚労省が過去に二回行っており、その結果は以下のとおりです。2020年末時点の人口はおよそ125.7百万人ですので（総務省）、0.68%ということは、その時点での抗体保有者はおよそ85万人と推察されます。

表1

抗体保有調査（厚労省HPより）	第一回（2020年6月1～7日）	第二回（2020年12月14～26日）
総検体数	7,950	15,043
陽性数	8	103
抗体保有率	0.10%	0.68%

 

一方、2021年5月5日現在、PCR検査陽性者数は約60万人（厚労省）です。これらの実績値より、昨年の5月30日で用いた感染係数と初期値を補正します。また、本年からはじまったワクチンの接種率を $c$ として微分方程式に取り込み、以下のように修正します。

$$\frac{dX}{dt}=a(X+Y+Z)-bX-βXY+γZ-cX\tag{1}$$ 

$${\frac{dY}{dt}=βXY-(α+b+v)Y} \tag{2}$$

$$\frac{dZ}{dt}=vY-(b+γ)Z+cX\tag{3}$$

ここで、$X$は抗体のないひとの数、$Y$は感染者数、$Z$は抗体のあるひとの数です。各係数は以下のとおりです。

表2

出生率	a	0.007	厚労省の人口動態調査（令和元年）
感染係数	β	0.01	2020年5月以降の厚労省データをもとに算出
感染致死率	α	0.017	死亡者数÷PCR検査陽性者数（2020年5月4日 厚労省）
免疫喪失率	γ	0.01	仮説
自然死亡率	b	0.011	厚労省の人口動態調査（令和元年）
ワクチン接種率	c	0.50	仮説
回復率	v	0.88	退院または療養解除者数÷PCR検査陽性者数（2020年5月4日 厚労省）
Xの初期値	X0	124.183	日本の人口-感染者数-治癒者数（百万人 2020年5月4日 厚労省）
Yの初期値	Y0	0.60763	PCR検査陽性者数（同上）
Zの初期値	Z0	0.53484	退院または療養解除者数（同上）

 

以上の初期値と係数を微分方程式　$(1)$～$(3)$ に代入して計算をした結果が図1 です。

図1

 

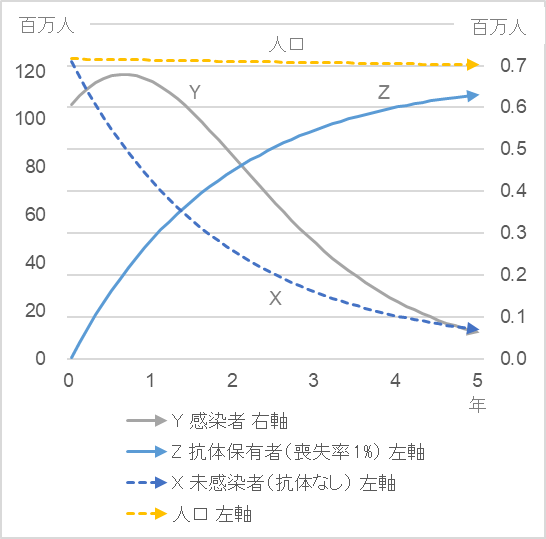
ワクチンの接種が進むことでPCR検査陽性者の数 $Y$ は急速に減少し、抗体をもつ人の数が五年後には人口の八割を超えることが分ります。免疫喪失率とワクチン接種率は現時点では仮の係数で計算していますが、感染係数同様、データを蓄積することで、より実態に近い係数に置き換えることができます。引き続きフォローしていきましょう。

計算の詳細にご興味のある方は、抗体 20210504 – Excel をご覧ください。

以上

 

 

 

記事一覧へ戻る