新型コロナウイルス感染症の収束が明らかになったのちは体内に抗体ができているかどうかに関心が移ると思われます。感染者が31万人を超えたアメリカのニューヨーク州で1万5千人を対象に行われた抗体検査の陽性率はニューヨーク市内でおよそ20%であったと公表されました(5月2日)。抗体保持者の割合が意外に多いと感じた方が多いのではないでしょうか。日本ではまだ大規模な調査が行われていないため抗体保持者の割合がわかりませんが、感染者数の推移を予測したように抗体保持者の割合も予測することができるでしょうか。今から41年前の1979年に「伝染病は人口を抑制するか?」というテーマに数理的に取り組んだふたりの学者(アンダーソンとメイ)の論文(Nature Vol.280)を参考に、この日本で何割のひとが新型コロナの抗体を獲得するのか?を予測します。なお、厳密には抗体を獲得したからといって免疫が保証されるわけではありませんが、ここでは議論を簡単にするために「抗体保持者=免疫獲得」とします。
基本理論
まず全人口を$X$、$Y$、$Z$ の三グループにに分類します。分類の仕方は以下のとおりです。
感染症を他人にうつす可能性のないひとで免疫のないひと (感受性者)→ $X$
感染症を他人にうつす可能性のないひとで免疫のあるひと (回復者=抗体保持者)→ $Z$
感染症を他人にうつす可能性のあるひと (感染者)→ $Y$
そして、この三つのグループがどのように相互に影響し合うかを数式に表します。
$${\frac{dX}{dt}=a(X+Y+Z)-bX-βXY+γZ} \tag{1}$$
$${\frac{dY}{dt}=βXY-(α+b+v)Y} \tag{2}$$
$${\frac{dZ}{dt}=vY-(b+γ)Z} \tag{3}$$
ここで、
$a$ は自然出生率 、$b$ は自然死亡率、$v$ は伝染病からの回復率、$α$ は感染による死亡率(以下、感染致死率)、$β$ は免疫のないひとが感染者に出会って感染する率、$γ$ は免疫を失う率、です。
$(1)$ 式は感染症にかかる可能性のあるひとの数 $X$ がどう変化するかを表しています。出生率 $a$ が $X$ だけでなく$Y$ と $Z$ にもかかっているのは生まれたばかりの子供はすべて感受性があると仮定しているからです。$X$ の減少要因は自然死 $b$ と感染者 $Y$との接触 $β$、増加要因は免疫の喪失 $γ$ です。
$(2)$ 式は感染していて他人にうつす可能性のあるひとの数 $Y$ の変化です。感染者の数 $Y$ は免疫のないひと $X$ と接触することによって増えますが $β$、感染による死亡 $α$、自然死 $b$、そして伝染病からの回復 $v$ という三つの要因によって減少します。症状の有無は問わずに、とにかくひとにうつす可能性のある人が $Y$ です。
$(3)$ 式は伝染病から回復するひとの数、つまり体内に抗体ができて免疫を獲得したひとの数の変化を表しています。回復率 $v$ で $Y$ から抜け出すことによって増加し、自然死 $b$ と免疫の喪失 $γ$ によって減少します。
アンダーソンとメイは以上の関係を分かりやすくまとめています。図1をご覧ください。
図1
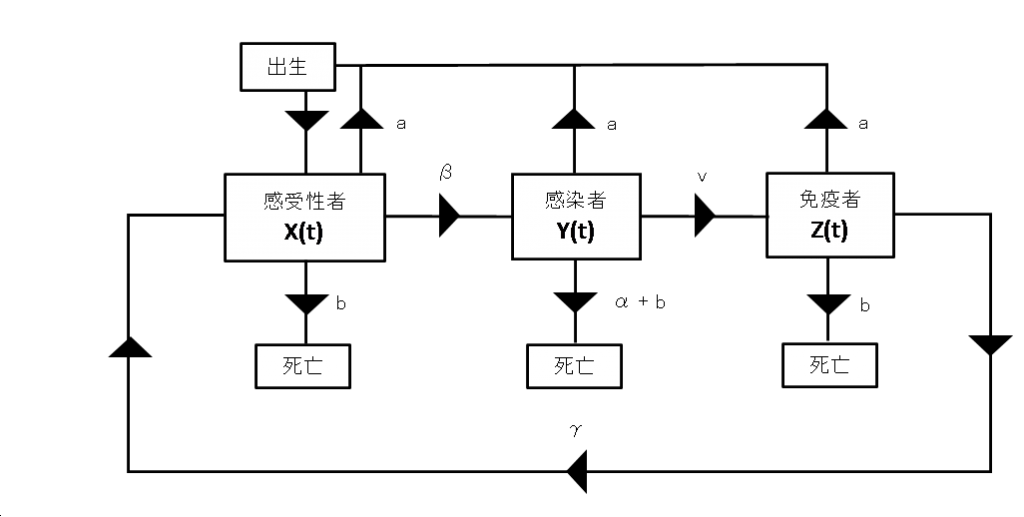
もし病気がなければ $$Y=Z=0$$ ですから、式$(1)~(3)$ は、式 $(4)$ に集約されます。
$$\frac{dx}{dt}=(a-b)X \tag{4}$$
$(4)$ 式は出生率 $a$ が自然死亡率 $b$ を上回れば人口はどこまでも大きくなり、下回れば限りなくゼロに近づくことを意味しています。
$X + Y + Z$ は全人口で、以後 $N$ とおきます。式 $(1)~(3)$ を足し算すると、
$${\frac{dN}{dt}=(a-b)N-αY} \tag{5}$$
となり、とてもシンプルな形になります。$a-b$ は病気のないときの自然増加率 $r$ です。人口とは、自然な増加から伝染病による死亡を差し引いた分だけ増えていくものだ、という単純なことをこの $(5)$ 式は示しています。
ではここで、方程式 $(1)~(3)$ の係数に任意の値を選んで $X$、$Y$、$Z$ がどのような動きをするのかをみていきましょう。式の中にはいろいろな係数が含まれていますが、$(5)$ 式から人口に影響を与える係数は $a$、$b$、$α$ の三つに絞られます。中でも$α$ が人口を抑制する係数ですからまずそこに焦点を当てましょう。表1をご覧ください。感染致死率が低いパターンとして、$α$ = 0.03、高いパターンとして $α$ = 0.5 を採用し、その他の係数はすべて同じにして計算すると、$X$、$Y$、$Z$ がそれぞれ時間とともにどう変化するかが分かります。図2-1、図2-2をご覧ください。オレンジの実線が人口 $(X+Y+Z)$、青の破線が感受性者(免疫なし)$X$、グレーの実線が感染者 $Y$、青の実線が回復者(免疫あり)$Z$ です。
動きの中で注目すべき点がいくつかあります。図2-1をご覧ください。伝染病が発生すると免疫をもたないひとXが感染しはじめますから、$X$ は減少し、感染者数Yは増加します。その後、$Y$ の中から回復者が現れることによって免疫をもつ$Z$ の数は増加します。興味深いのはある程度時間が経過すると感染者$Y$ と回復者Zが漸増する一方で、免疫をもたないひと $X$ の増減が止まり平衡する(増えも減りもしなくなる)という点です。人口は、感染者 $Y$ と免疫をもつ回復者 $Z$ の増加によって増え続けます。その結果、感受性者 $X$ の人口に対する割合は徐々に減少する、つまり伝染病にかからない人の割合が徐々に増えるということですから、社会が少しずつよい方向に向かうことを意味します(図3-1)。ちなみに感染者の割合も増えますが、感染者には無症状のひとも含まれてますので全員が病気に苦しんでいるわけではないことに留意する必要があります。
一方、感染致死率 $α$ が高いと、人口は減少に転じます。これは式➅からも想像がつきます。ここで興味深いのは、感染致死率 $α$ が高いと、免疫獲得者の割合が低くなってしまうという現象です。図3-2をご覧ください。$α$ = 0.03 のときは抗体保持者が六割近くに達しているのに、$α$ = 0.5 では3.5%程度に留まっています。②式より、感染致死率 $α$ が高いと感染者 $Y$ の数が減少することが分かります。$Y$ の数が減ると、③式より免疫保持者 $Z$ の数も減ります。免疫獲得者を増やすためには感染源を確保しておく必要があるのです。
表1
| 図2-1 | 図2-2 | ||
| 出生率 | $a$ | 0.25 | 0.25 |
| 感染係数 | $β$ | 0.015 | 0.015 |
| 感染致死率 | $α$ | 0.003 | 0.500 |
| 抗体損失率 | $γ$ | 0.01 | 0.01 |
| 自然死亡率 | $b$ | 0.24 | 0.24 |
| 回復率 | $v$ | 0.45 | 0.45 |
| $X$ の初期値 | $X_{0}$ | 100 | 100 |
| $Y$ の初期値 | $Y_{0}$ | 0.001 | 0.001 |
| $Z$ の初期値 | $Z_{0}$ | 0.001 | 0.001 |
図2-1 図2-2
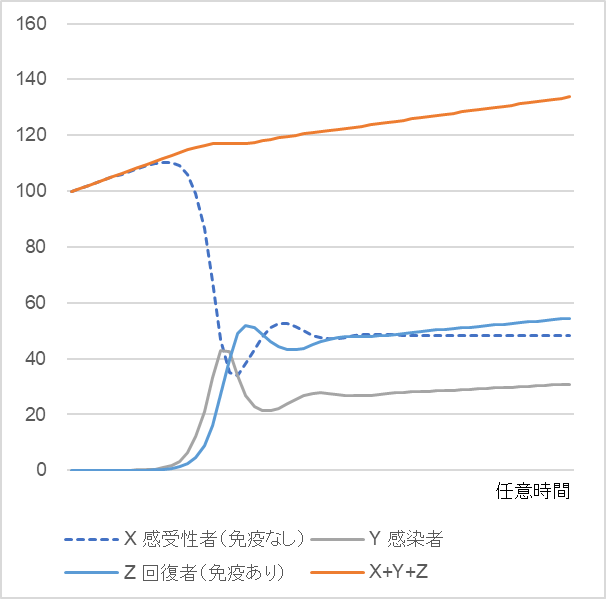
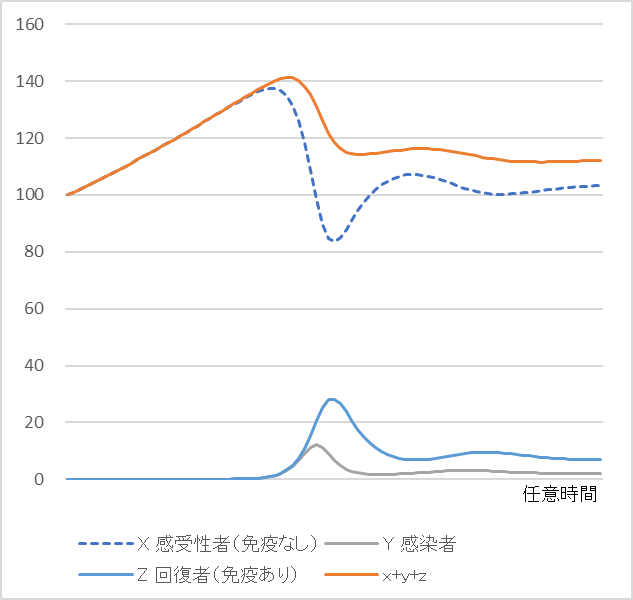
感染致死率 $α=0.003$ 感染致死率 $α=0.500$
図3-1 図3-2
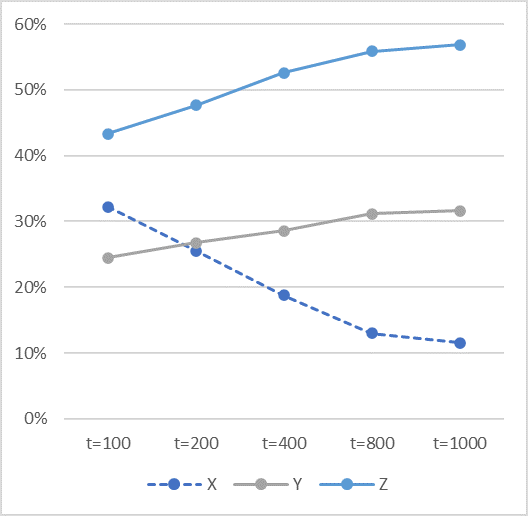
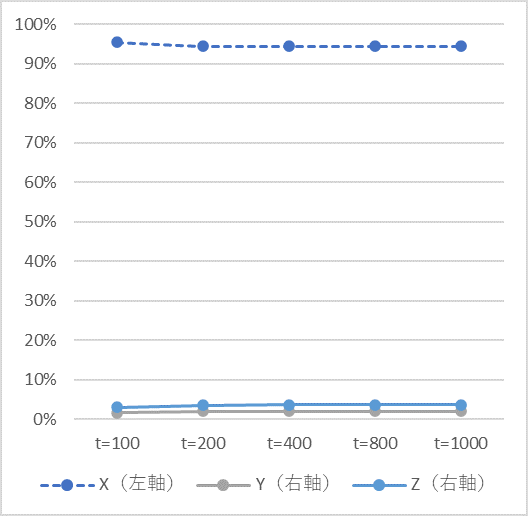
感染致死率 $α=0.003$ 感染致死率 $α=0.500$
<他の係数が気になる方へ>
感染係数 $β$:大きいと全体の動きだし($X$、$Y$、$Z$の増減)が起こるタイミング)が速くなり小さいと遅くなります。
抗体喪失率 $γ$:大きいと感染者数Yと回復者数Zの増え方が少なくなり、小さいと大きくなります。
回復率 $v$:大きいと動き出しが遅くなり、$X$ の平衡値が高くなります。逆に小さいと動き出しが速くなり $X$ の平衡値が低くなります。
では、上記の計算方法を使ってを今後の日本の状況を予測してみましょう。新型コロナウイルスの感染者数、死亡者数、回復者数は厚労省から公表されている2020年5月28日現在の数字としています(参考資料1)。出生率と自然死亡率は厚労省の人口動態調査(令和元年、参考資料2)に依ります。免疫喪失率についてはデータがありませんので1%と10%の二通りで計算しました。高い方を10%にしたのは、新型コロナウイルスは一度陰性になっても再度陽性になることがあると報道されているためです。日本の人口は総務省のホームページ(2020年予測)を参照しました。
これですべての係数と初期値が出揃いました(表3)。これらの数値を式 $(1)~(3)$ に代入すれば時間推移が計算できます。図4をご覧ください。青色の破線が感染の可能性がある感受性者X(右軸)の推移です。人口の自然減とともに、125百万から123百万人に減少します。黄色の実線が抗体喪失率1%のときの抗体獲得者、青色の実線が同喪失率10%のときの抗体保持者の数です。
表3
| 出生率 | $a$ | 0.007 | 厚労省の人口動態調査(令和元年)より |
| 感染係数 | $β$ | 1.6683×10-4 | 厚労省公表のPCR検査陽性者数の人口比 |
| 感染致死率 | $α$ | 0.052 | 厚労省公表の死亡者数÷感染者数 |
| 抗体喪失率 | $γ$ | 0.1 or 0.01 | 仮説 |
| 自然死亡率 | $b$ | 0.011 | 厚労省の人口動態調査(令和元年)より |
| 回復率 | $v$ | 0.848 | 厚労省公表の退院または療養解除者数÷PCR検査陽性者数 |
| Xの初期値 | $X_{0}$ | 125,294 | 現時点の日本の人口(百万人)総務省予測 |
| Yの初期値 | $Y_{0}$ | 0.01668 | 現時点の感染者数(厚労省) |
| Zの初期値 | $Z_{0}$ | 0.01415 | 現時点の退院または療養解除者数(厚労省) |
図4

免疫のない感受性者X(破線)は人口の自然減とともに減少します。感染者(グレーの実線)が指数関数的に減少する一方で抗体獲得者(黄色と青色の実線)は増加します。
ではここで抗体獲得者 $Z$ に注目します。初期値を参考資料1の「退院または療養解除となった者の数」とすると五年後の数は表4のとおりですが、
表4
| 抗体保持者の数 | 初期値 | 5年後 | 人口比 |
| 抗体喪失率 = 10% のとき | 14,100 | 18,300 | 0.015% |
| 抗体喪失率 = 1% のとき | 14,100 | 27,000 | 0.021 |
はじめに、で触れたようににニューヨーク市街地では二割のひとが抗体検査に陽性を示した事実は無視できません。仮に、生活環境や習慣の違いを踏まえて、日本における抗体保持者比率を百分の一の 0.2% とすると現時点での抗体保持者はおよそ25万人(125百万人 x 0.2%) となります。これは現状の回復者1万4千人のおよそ18倍です。よって、ざっくりと感染者 $Y$(無症状を含む)と抗体をもつ回復者 $Z$ の初期値を現状の20倍にしてみましょう。図5 と表5 をご覧ください。抗体喪失率が1%の場合、5年後の抗体獲得者数は 54万人、同喪失率が10% の割合は36万人とでました。いずれにしても人口比では1%以下です。
図5
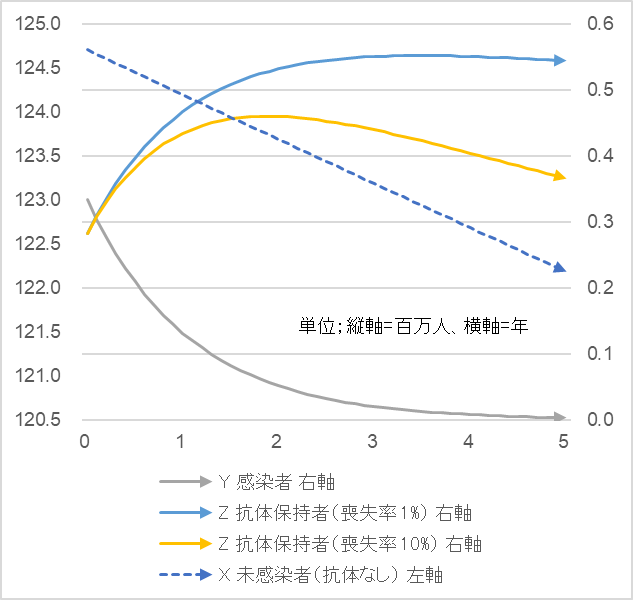
表5
| 抗体保持者の数 | 初期値 | 5年後 | 人口比 |
| 抗体喪失率 = 10% のとき | 283,000 | 366,000 | 0.291% |
| 抗体喪失率 = 1%のとき | 283,000 | 544,000 | 0.432% |
さいごに
免疫は実際にウイルスに感染するか、ワクチンを打ってもらうかのいずれかでしか獲得することはできません。しかもウイルスは絶えず進化しています。DNA形が少し違うだけで免疫系はもう機能しません。今から100年前にはやったスペイン風邪(インフルエンザ)は世界で5億人が感染し5千万人死亡したといわれています。その第一波(1918~1919)で日本人は2100万人が感染し26万人が死亡しました。第二波(1919~1920)では、240万人が感染し、13万人が死亡、さらに、第三波(1920~1921)では22万人が感染、3700人が死亡しています。毎年のように感染者数が波打つ原因はウイルスが微妙に変化(進化)していることが原因と推察されています。(参考資料3)。
新型コロナウイルスの感染者は2020年5月現在、世界でおよそ590万人、死者36万人に達しました。スペイン風邪に比べると二桁くらい規模が小さいですが、注目すべきはパンデミックが起こるタイム・スパンが100年もあったことです。東日本大震災級の規模の地震は1000年に一度といわれています。これらを同時に経験した我々稀有な世代は後世に警鐘を鳴らすべき立場にいるのかもわかりません。今後行われるであろう調査や検査データを計算式に取り込むことによってキーとなるパラメーターも同定できるようになるでしょう。そうすれば、いずれまたやってくるパンデミック時の政策決定に寄与できるようになると思われます。
計算の詳細にご興味のある方は、抗体 20200530 – Excel をご覧ください。
おわり
<追記>
つづきは、2021年5月5日づけのブログ「コロナウィルスの抗体保有者数の数理予測」をご覧ください。

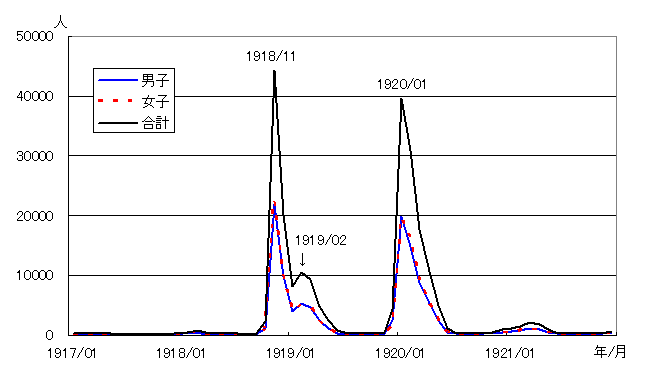
スペイン風邪による死亡者数の月別推移(東京健安研セ年報 56, 2005)