2022年7月18日付けのブログ、シンプルな数式が産み出す「数理アート」で、以下の数式を座標に表すと、とても興味深い「非対称」な形があらわれるという話をしました。
$$x^3+y^2=x\tag{0}$$
図0
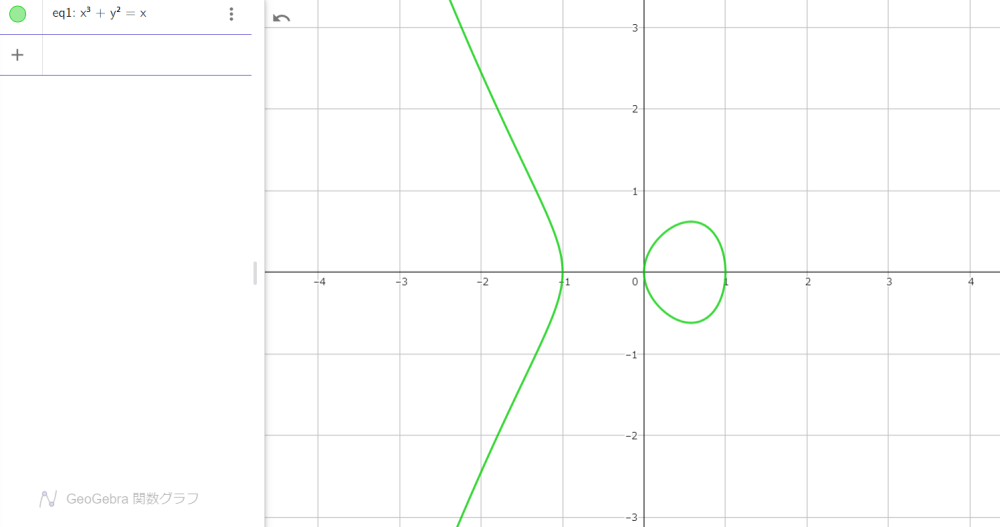
横軸が $x$、縦軸が $y$
首を少し傾げると、山の頂から昇る朝日のように見えます。「山の曲線も、大気の影響で変形する太陽も、リアル」と感想を述べただけでしたが、本日はこの方程式を掘り下げます!
まず、式 $(0)$ を変形します。
$$y^2=x-x^3=x(1-x^2)=x(1+x)(1-x)\tag{1}$$
こうすると、このグラフが 間違いなく整数座標の $(-1,0)$, $(0,0)$, $(1,0)$ の三か所を通ることが分かります。このなかで山頂にあたる $(-1,0)$ に注目します。なぜなら、そこには間違いなく絶景が拡がっているはずだからです。視線を表すために、山の両裾野と太陽へ接線を引いてみましょう。もちろん定規でさっと引くこともできますが、「接線といえば微分」ですから、なにはともあれ、式 $(1)$ を $x$ で微分します。途中の計算式は省略させていただいて、結果だけ示すと
$$\frac{dy}{dx}=\frac{1-3x^2}{2\sqrt{x-x^3}}\tag{2}$$
になります。一方、座標 $(-1,0)$ と任意の座標 $(x,y)$ を通る直線の傾きは、
$$\frac{(0-y)}{(-1-x)}=\frac{y}{1+x}\tag{3}$$
です。式 $(2)$ と式 $(3)$ が等しいこと、さらに、式 $(1)$ より
$$y=\sqrt{x-x^3}\tag{4}$$
であることから、以下の等式が得られます。
$$\frac{1-3x^2}{2\sqrt{x-x^3}}=\frac{\sqrt{x-x^3}}{x+1}\tag{5}$$
整理すると、
$$x^2+2x-1=0\tag{6}$$
とシンプルな $x$ の二次方程式になりますので、同方程式の解の公式から、
$$x=-1±\sqrt{2}\tag{7}$$
が得られます。これが接線が山と太陽に接する $x$ の座標です。あとは、この $x$ を式 $(4)$ に代入すると、
$$y=±\sqrt{6±4\sqrt{2}}\tag{8}$$
が得られます。接点は $x$ 軸に二か所、$y$ 軸に二か所、合計四か所、具体的には、次の四座標です。
$$(-1-\sqrt{2},-\sqrt{6+4\sqrt{2}})\tag{接点A}$$
$$(-1-\sqrt{2},\sqrt{6+4\sqrt{2}})\tag{接点B}$$
$$(-1+\sqrt{2},\sqrt{6-4\sqrt{2}})\tag{接点C}$$
$$(-1+\sqrt{2},-\sqrt{6-4\sqrt{2}})\tag{接点D}$$
接点座標にはすべて $\sqrt{2}$ が入っているので無理数であることが分かります。$\sqrt{2}=0.14142$ とおいて、図0に接線と接点を描き加えます。
図1
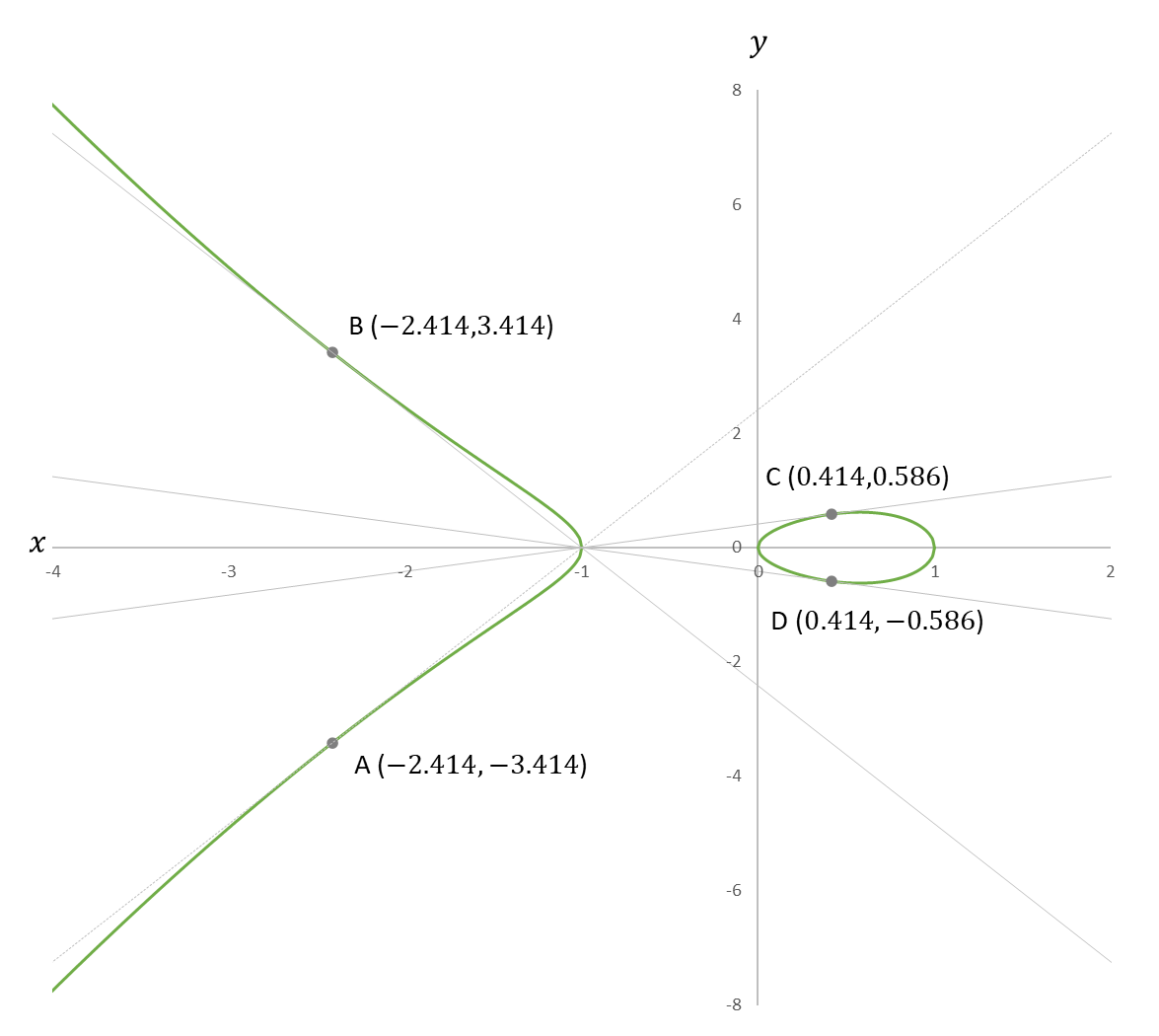
山の裾野と接線が重ならないように $x$ 軸と $y$ 軸のスケールを調整しています。
座標 $(-1,0)$ から四本の接線が後光の様に放射されています。山の裾野が優雅な曲線を描いていて、接点の位置が絶妙です。
ところで、なぜ $-1<x<0$ と $1<x$ には図形が存在しないのでしょうか.
式 $(1)$ より、
$$y=\sqrt{x(1+x)(1-x)}\tag{9}$$
ですから、$-1<x<0$ と $1<x$ のときは ルートの中が負の値になることが分かります。つまり、その間は $y$ が虚数になるので、実数軸のグラフには現れないということです。逆にいえば、虚数軸を追加すれば現れるということですから、$y$ 軸を虚数軸 $z$ に入れ替えてみましょう。
図2
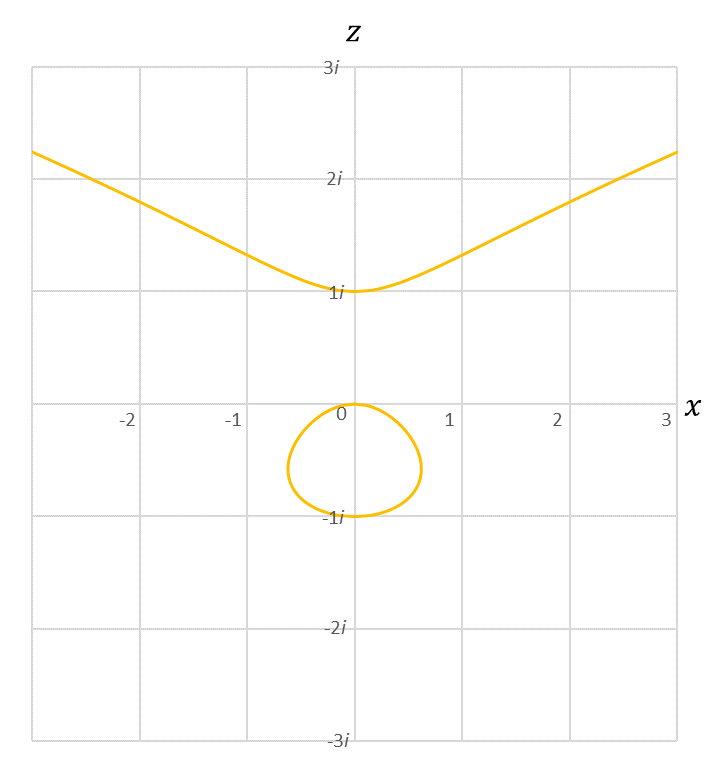
図0の $y$ 軸を虚数軸 $z$ に入れ替えた図
確かに現われました、しかも同じ「山と太陽」の組み合わせが!
図0と図2を合体して三次元の $xyz$ 座標にしてみましょう。図2の $x$ 軸を図1に揃えるべく、「ぐぐっ」と回転させて、見る角度を三次元的に変えます。
図3
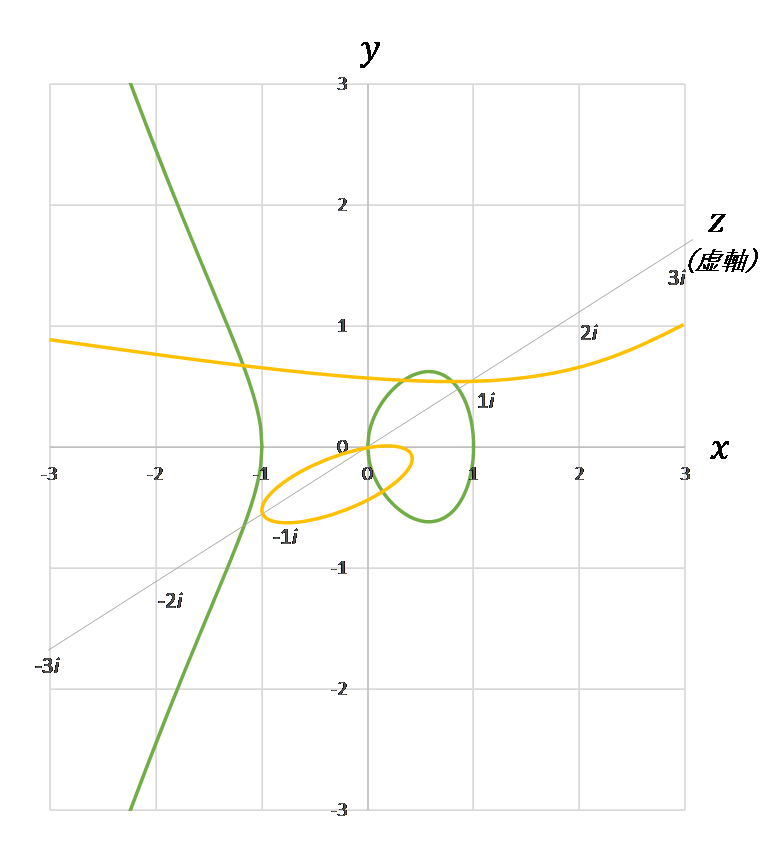
楕円曲線 $x^3+y^2=x$ の $xy$ 座標に虚軸 $z$ を加えると、隙間を埋めるようにもうひとつの楕円曲線が現われる。
虚軸 $z$ に沿って現れる黄色の楕円曲線は私が手書きで描き加えたものですので正確ではありません。ただ、こうすることによって、何もないと思っていたところに、実は双子の兄弟がいた!ことが視覚化できます。-1<x<0 と 1<x は、ぽっかりと空いていたわけではなく、しっかりと埋まっていたのです。
おわり
記事一覧へ戻る