2023年1月8日付のブログ「株価の動き」を「数式化」するひとつの方法で、世界の株価指数の動きが以下の微分方程式で表現できることを示しました。
右辺の第一項が拡散、第二項が移流です。$D$ と $C$ はそれぞれの速度係数です。この式(1)の展開例が図1です。ある一定期間の株価の分布はおおよそ正規分布に従うことがわかっていますが、その正規分布が時間経過とともに、グレー、オレンジ、ブルー、グリーンと拡散しながら移流しているのがわかります。
図1


確率分布曲線(正規分布)の拡散移流。移流係数 $C$ が負のときは右へ、正のときは左へ移流する。
では実際の社会現象を観察してみましょう。図2が世界の株価指数の過去四年間の推移です。
図2

世界の株価推移(2021年~2024年の日次終値、2021年1月4日=1.0とした)
七色のインクを橋の上から同時に川の同じ場所に落とし続けたら、このような絵になりそうですが、この図2を図1の様式に書き換えてみましょう。図3をご覧ください。明らかに拡散を続けていることがわかりますし、よく見ると、左右にわずかに移流していることもわかります。
図3
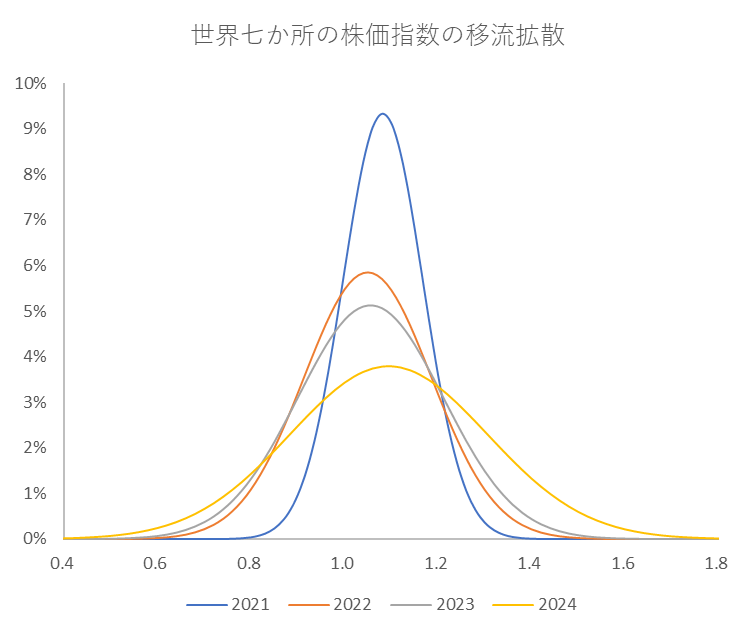
2021年初から各年度末までの平均と分散で描いた世界の株価指数の正規分布の推移。
拡散しながら左右にわずかに移流している様子がわかる。
図4は個別銘柄(ブリヂストン、資生堂、三菱UFJ、トヨタ自動車、ソフトバンク)と TOPIX の動きです。図2同様、2021年初の株価を 1.0 に揃えた過去四年間の日次終値の推移です。
図4
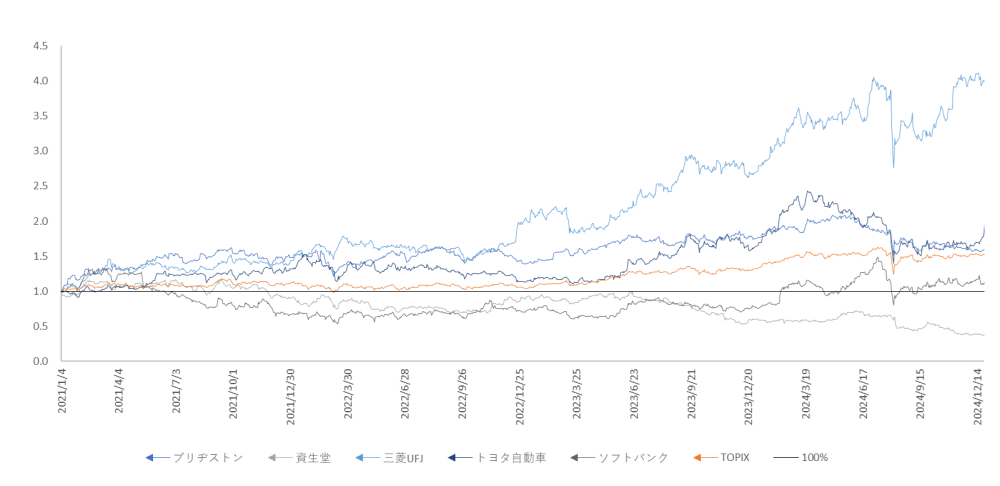
2021年~2024年の国内個別銘柄とTOPIXの推移(2021年初=1.0)
正規分布で置き換えると、
図5

2021年初から各年度末までの平均と分散で描いた個別銘柄の正規分布の推移。
拡散しながら移流している様子がよくわかる。
となります。図1を見比べてください。よく似ています。
ところで、図3(世界の株価指数の分布推移)と図5(国内の個別銘柄の分布推移)をよく観察すると、移流係数 $C$ と拡散係数 $D$ は一定ではなく絶えず変化していることもわかります。全体が右肩上がりの年は右方向へ、右肩下がりのときは左方向へ移動しています。各銘柄の成長のばらつきが大きくなればなるほどベルカーブの高さが低くなり裾野が広がっています。
つづく
記事一覧へ戻る