株価に限らず、通貨でも、金属でも、クラッシュや破壊が生じるクリティカルなタイミングを $t_c$ としたとき、そこへ至るまでの過程をよく観察し、数値化することで $t_c$ は予測できるとする理論をご紹介します。私はこれまでの研究で株価の暴落はランダムに起こるものであって、その引き金や経済環境などの説明は後付けに過ぎないとして、その理由を確率微分方程式を使って解析してきました。ただ、これでは残念ながら暴落がいつ起こるのかを予測することはできません。

一方、ディディエ・ソーネット 教授（フランス人、スイス連邦工科大学チューリッヒ校、起業家リスク議長）はその理論をアリアン・ロケットの主要部品の破損診断に応用して成功した科学者で、複雑系理論をベースにべき乗則と対数周期を組み合わせた数式で $t_c$ （the critical time) を具体的に予測します。ちなみに、同教授は極端なクラッシュや破壊をもたらすものを「ドラゴン・キング」と呼んでいます。$t_c$ とはそのドラゴン・キングが現れる瞬間です。

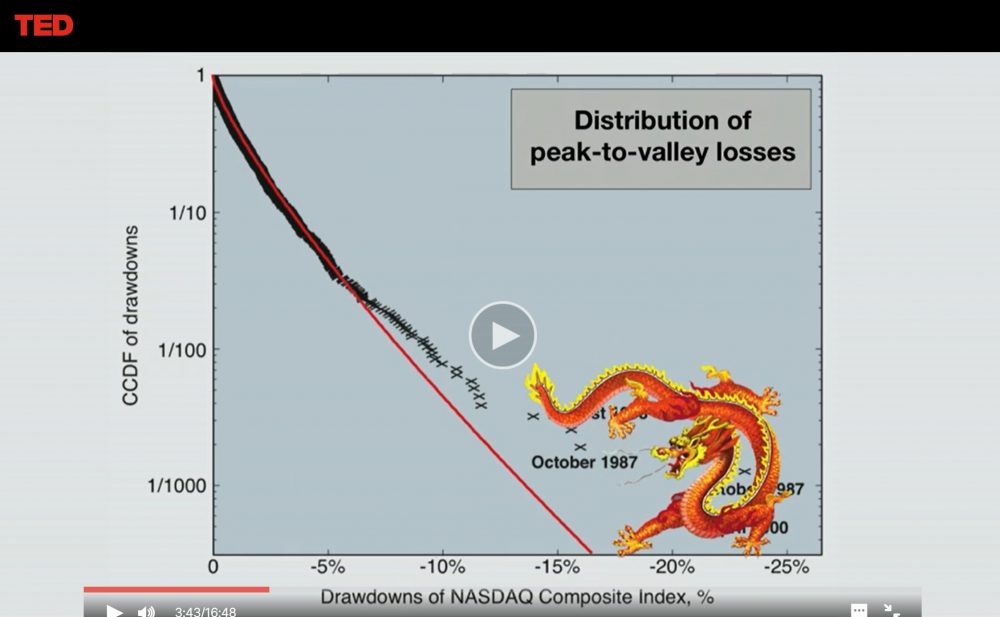
フィナンシャル・マーケットに時折現れるドラゴン・キング

Didier Sornette　TEDGlobal 2013　”How we can predict the next financial crisis”より

 

 

では早速、数式をみていきましょう。（数式は同教授の著書 “Why Stock Markets Crash” Critical Events in Complex Financial Systems から引用しています。）

まずべき乗則ですが、同法則は英語で Power Law ですのでその時間関数を $F_{pow}(t)$ と表現します。

$$\begin{array}{}\text{(１)}& F_{pow}(t)=A+B(t_c-t{)}^m\end{array}$$

クラッシュの代表例として1987年10月のブラックマンデーを選びます。グレーの破線はエクセルで自動表示できる指数近似曲線です。オレンジの曲線が $(1)$ 式で描いたものです。比較するとグレーの破線よりもオレンジの実線の方がバブル崩壊前の立ち上がりをよりよく近似しているのが分かります。

次に対数周期ですが、これは $t_c$ に向けて波の間隔がより短くなることを表現しようとするものです。対数周期は英語で Log Period ですからその時間関数を $F_{lp}(t)$ と表現します。

$$\begin{array}{}\text{(2)}& F_{lp}(t)=1+C\cos (\omega \log ((t_c-t)/T))\end{array}$$

アップダウンをコサイン波で、波長の時間変化（短縮化）を対数で表していますね。図1の紫色の実線が $(2)$ 式で描いた波形です。

図1

A= 412, B = -158, m=0.4, C = 0.3, ω = 9.0, T = 1.0, t_c =  1987.82（1年=1.0)

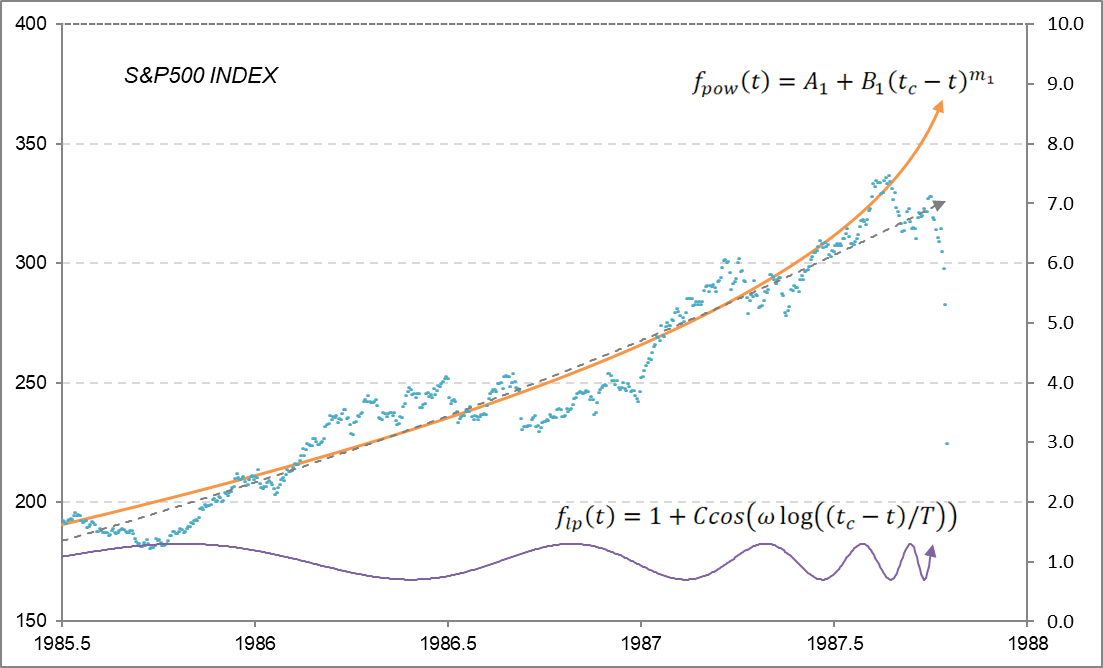
そして、クラッシュにいたる株価の推移は $(1)$ 式と $(2)$ 式を掛け合わせることで表現できるというわけです。つまり、

$$\begin{array}{}\text{(3)}& F_{lp}(t)=A+B(t_c-t{)}^m[1+C\cos (\omega \log ((t_c-t)/T))]\end{array}$$

です。この $(3)$ 式がドラゴン・キングの出現を予測する数式です。図2 をご覧ください。

図2

A= 412, B = -158, m=0.4, C = 0.075, ω = 9.0, T = 1.0, t_c = 1987.82（1年=1.0）

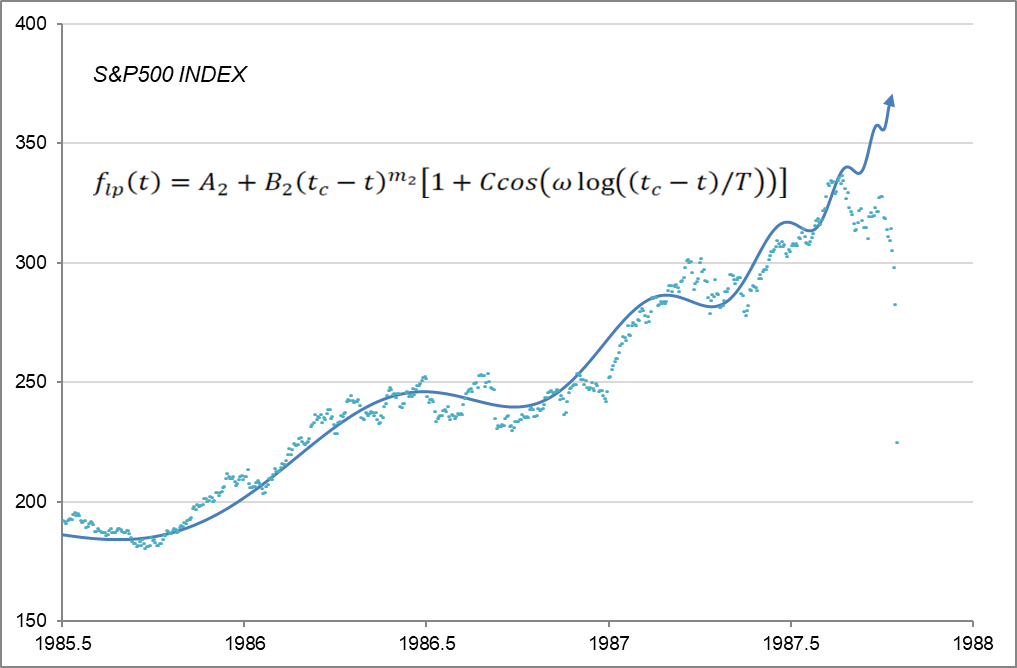
ランダムに動いていると思っていた株価が、なんと一定の関数で近似されてしまうとは驚きです。しかも、二年前からクラッシュへの歩みがはじまっていることを示しています。

さて、すでにお気づきになられた方もおられると思いますが、式 $(3)$ を使って図2を描くには予め $t_c$ を決めておく必要があります。予測したい $t_c$ が最初から分かっているのであればそもそも予測する必要はありませんね。そうではなくて、株価の動きに式 $(3)$ をうまくフィッティングする過程で $t_c$ が自ずと決まる、つまり、理論を現実に重ね合わせると ドラゴン・キングが見えてくる、ということです。では、具体的にやってみましょう。

仮に今、我々は 2019年末にいるとします。その時点で S&P500 は 2018年末に比べ 30% 以上値上がりしていました。そこで、式 $(3)$ の各種パラメーターを入れ替えて、なるべく実態に沿うようにフィッテング作業を行います。上下運動の激しかった 2019年の前半はひとつの波に集約して、後半を第二波、第三波で表現しようとすると $t_c$  を 2020.12 に設定する必要があります（図3）。結果として、およそ二か月後にはバブルが崩壊するという予測をしたことになります。

図3

A= 3,820, B = -1,150, m=0.77, C = 0.03, ω = 15.5, T = 0.58, t_c = 2020.12（1年=1.0）

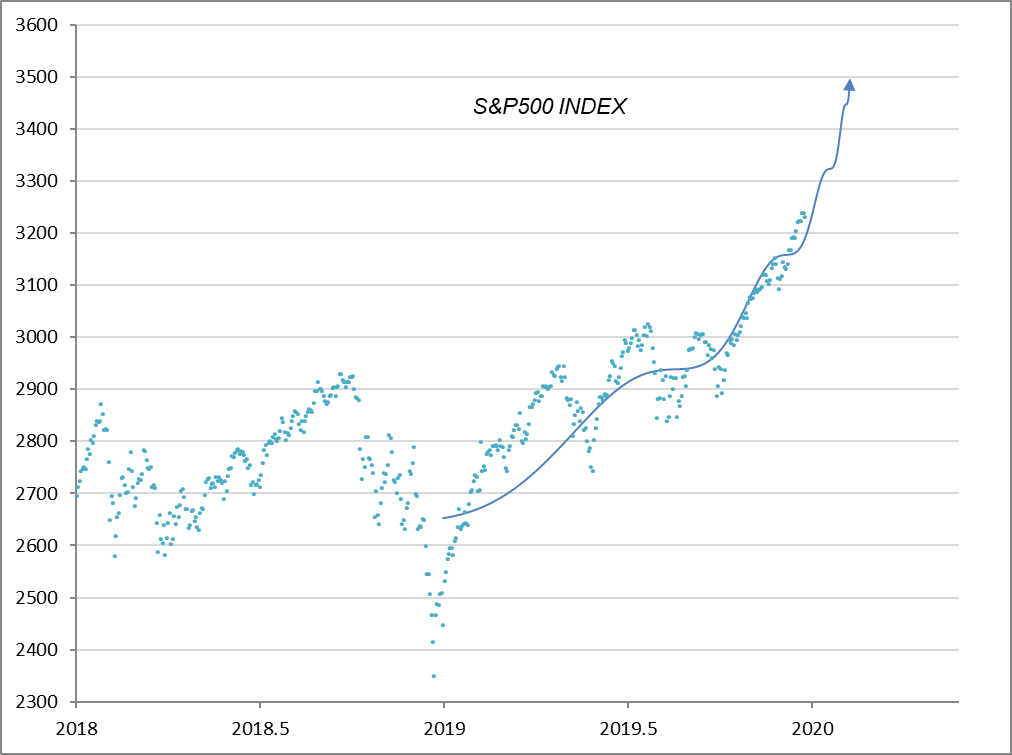
さて、その後、実際の株価はどう推移したでしょうか。図4をご覧ください。2020年2月19日に 3,386.10 の最高値を付けたあとクラッシュしました。

図4

A= 3,820, B = -1,150, m=0.77, C = 0.03, ω = 15.5, T = 0.58, t_c = 2020.12（1年=1.0）

過去のデータを使うと先の結果がみえているため恣意的にパラメーターを操作したのではないかと思われても仕方がありません。そこでソーネット教授は予測結果に鍵をかけておき、あとで検証できるようにしました。さらには FCO (Financial Crisis Observatory) というバブルをリアルタイムで観測するプラットホームを創設してその予測状況を公開しています。以下のウェブサイトご覧ください。

ちなみに、最新の報告書（2021年2月1日付）によると S&P500　（Broadcastingセクター） は昨年の 10月（図5の緑の縦線の右側）からバブル期に入っていると予測されています。

図5

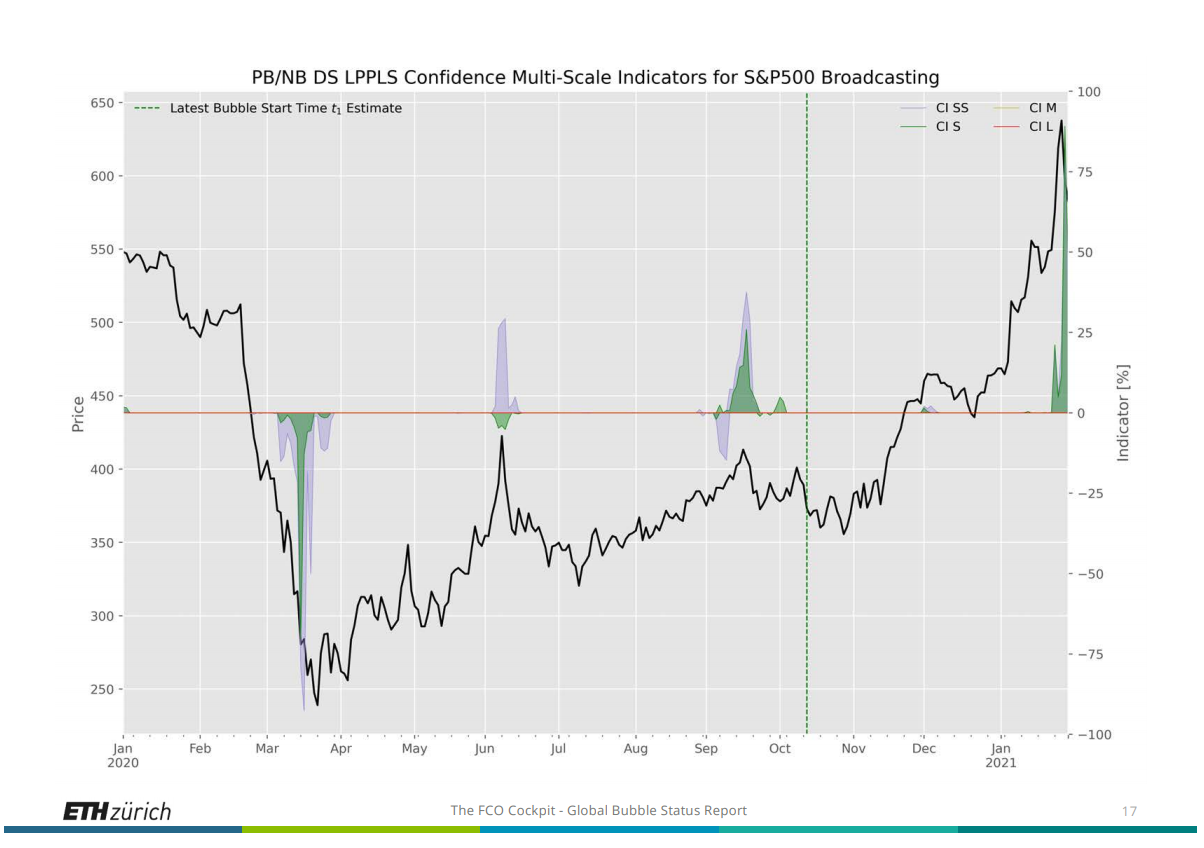
つづく

 

＜追記＞

計算の詳細にご興味のあるかたは、対数周期曲線 – Excel をご覧ください。

「後編」は、2021年2月15日付のブログ 、2021年3月14日付のブログ をご覧ください。

 

＜参考文献＞

Didier Sornette, Why Stock Markets Crash, Critical Events in Complex Financial Systems, Princeton University Press, 2003

 

記事一覧へ戻る