2022年11月19日付けのブログで「世界一美しい等式 $e^{i\pi}=-1$」を導出しましたが、本日は「最も有名なアインシュタインの式」としてTシャツにも印刷されることがある $E=mc^2$ の導出にチャレンジします。「イー・イコール・エムシー・ジジョウ」と語呂がよくて覚えやすいだけでなく、エネルギー $E$、質量 $m$、光速 $c$ という、まったく異質なものが等式で結ばれていること、しかもこの数式が大量破壊兵器や原子力発電所など、身近に存在する危うさの理論的根拠である、という点が他の数式を寄せ付けない知名度につながっているように思えます。

まずは下の図をご覧ください。

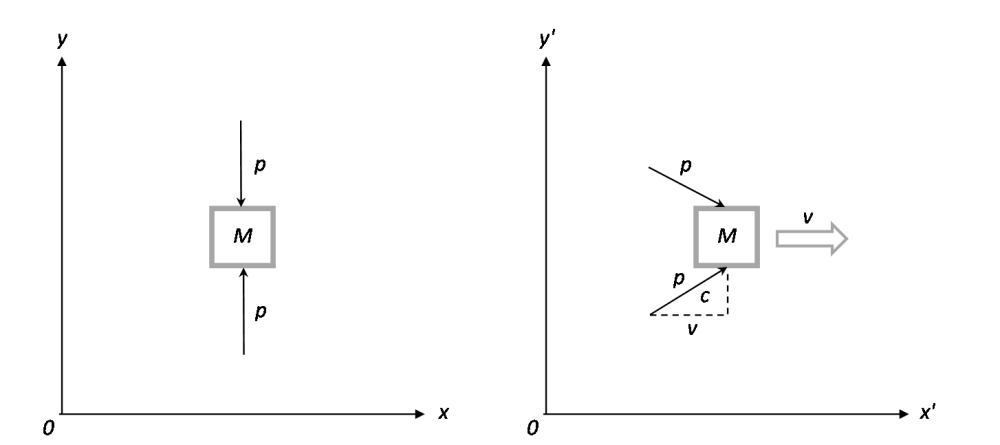
         　　　　　速度 $v$ で飛行中のロケットの中にいる Ａ さんの座標　　　　　           　　　　　　　 　　 ロケットの外で静止している B さんの座標

 

図1 は速度 $v$ で飛行中のロケットの中にいる A さんの座標、図2 がロケットの外で静止している B さんの座標です。図1 において、ロケットの中で静止している物体 M に同時に上下逆方向から運動量 $p$ の光子が吸収されたとします。物体 M は速度 $v$ で移動しているので、B さんは光子が斜めに物体 M に吸収される様子を観測します。このとき、光子の運動量 $p$ は M に斜めに当たる分小さくなり、その割合は三角形の相似より、$\frac{v}{c}$ です。

ところで、光子の運動量 $p$ は、光子のエネルギー $ε$ を光速 $c$ で割ったもの、つまり、

$$p=\frac{ε}{c}\tag{1}$$

であることがわかっています（ウィキペディア「光子」参照）。

以上より、物体 M の運動量の増加分は、二個の光子が斜め吸収されることから、

$$\frac{2ε}{c}\frac{v}{c}=\frac{2εv}{c^2}\tag{2}$$

となります。

一方、運動量は、質量に速度をかけたもの、というのが定義です。B さんからみる物体 M は一定の速度 $v$ で移動しているので、物体 M が光子二個を吸収して運動量を増やしたのであれば、その増加分は速度 $v$ が同じなら質量の増加として現れなくてはなりません。増えた質量を $m$ とすれば、運動量の増加分は $mv$ です。

これで運動量の増加分が二通りで表現できたことになり、これらを等式で結び合わせると、

$$\frac{2εv}{c^2}=mv\tag{3}$$

変形して、

$$2ε=mc^2\tag{4}$$

$2ε$は物体のエネルギーの増加分 $E$ なので、

$$E=mc^2\tag{5}$$

となり、最も有名なアインシュタインの式に辿り着きました。

 

中学・高校で習ったとおり、エネルギーは「力ｘ距離」で、力は「質量ｘ加速度」ですから、エネルギーは「質量ｘ加速度ｘ距離」です。これを「単位」に置き換えると、「キログラム x メートル/秒² x メートル」、つまり「キログラム x メートル²/秒²」です。メートル²/秒² は速度の二乗ですから、「エネルギー＝質量ｘ速度²」となります。冒頭でアインシュタインの式は「異質なものの組み合わせ」と述べましたが、単位の組み合わせを替えるだけでその「からくり」が垣間見えるのも興味深いところです。

 

おわり

 

＜参考文献＞

「世界は2乗でできている」小島寛之著、2013、講談社ブルーバックス

 

 

記事一覧へ戻る