シリーズでお伝えした2021年9月3日付ブログ「コロナ禍の売上急落の不安を払拭する超簡単な数式」、 同年9月11日付のブログ「継続は力なりを数式で理解する」、そして同年9月13日付のブログ「経営者が目線を上げる、という数理的意味」は時系列分析を事業の売上に適用したものでした。

$$x_{t}=αx_{t-1}+µ+ε_{t}\tag{1}$$

x_t は時間 t における売上、 x_t-1 はそのひとつ前の売上です。α は売上係数、µ は定数。ε_t はノイズ項です。この単純な数式が、たとえば、一時的に急伸した売上もその後必ずもとの状態にもどること、を教えてくれました。

式（1）は、そのルールに基づき展開すると、

$$x_{t}=αx_{t-1}+µ+ε_{t}=α^tx_{0}+µ(1+α+α^2+α^3+ ・・・+α^t)+(α^{t-1}ε_{1}+α^{t-2}ε_{2}+α^{t-3}ε_{3}+・・・+ε_{t})\tag{2}$$

となり、それぞれの項には以下の性質があります。

第一項： $α^tx_{0}$ は、$α<1$ のときゼロに近づく

第二項： $µ(1+α+α^2+α^3+ ・・・+α^t)$ は $α<1$ のときある一定の値に収束する

第三項： $α^{t-1}ε_{1}+α^{t-2}ε_{2}+α^{t-3}ε_{3}+・・・+ε_{t}$ はノイズの集まりで正規分布する

たとえばコロナ禍は、第三項の一時期に大きなマイナスのノイズを与えると再現できますし、逆に、売上の急伸は、一時期的に大きなプラスのノイズを与えると再現できます。そして、いずれの場合も刺激が過ぎ去ると元の状態に戻ります。第二項の µ が大きいか小さいかによって、収束する値が大きく変わるので、この µ こそが経営者の目線と捉えることができる、というような話をしました。

たとえば、t=0 のときの売上 x₀ を 100 、売上係数 α を 0.9、定数 µ を 10 とします。ランダム項の ε_t は平均 0、標準偏差 5 の正規分布に従うとします。そうすると、売上 x_t の時系列変化は図１のようになります。

図１

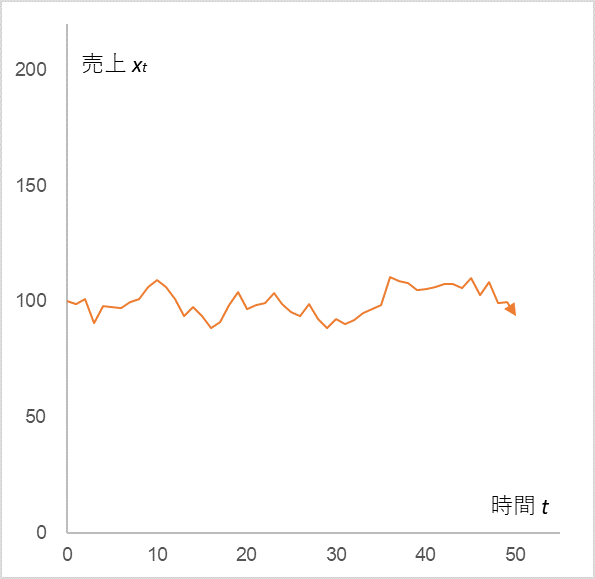
初期売上 x₀=100, 売上係数 α=0.9, 定数 µ=10, ランダム項 ε_t=（平均 0、標準偏差5）の確率正規分布

 

売上 100 を中心にして上下運動しています。ここに、t=10～13 でマイナスのノイズを入れると図２のようになります。

図２

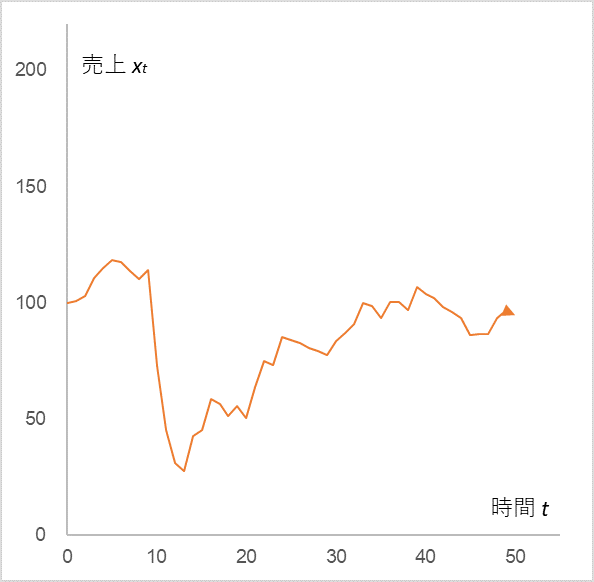
x₀=100, α=0.9. µ=10, ε_t は 図1と同じ正規分布に従うランダム項。但し、ε₁₀=-40, ε₁₁=-30, ε₁₂=-20,ε₁₃=-10

 

マイナスのノイズを入れることで売上は急落しますが、またもとに戻っていくのが分かります。

さて、今年（2024年）の日経平均は8月に入った途端に二割急落しました。これは1987年のブラックマンデーや2008年のリーマンショックに匹敵する下げです。図３をご覧ください。

図3

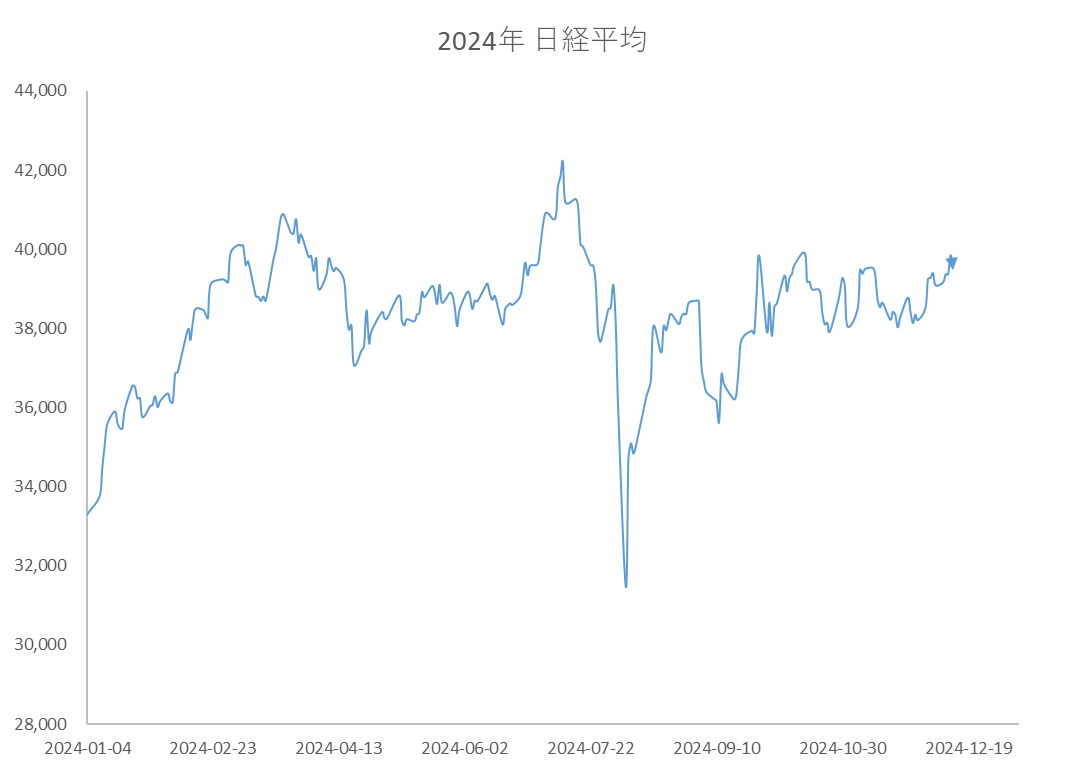
日経平均は2024年8月1日、2日、5日の三日間で21%急落した。これは1987年10月19日のブラックマンデー（-15%）、2008年10月8～10日のリーマンショック（-24%)に匹敵する。

 

ではここで、ものごとを逆から見ます。今年の日経平均株価の急落を時系列分析で再現できるでしょうか？それはつまり、式（１）のパラメーター（$α$と$μ$）を調整することによって、図２を図３に近づけることができるか？という問いと同じです。

さっそくやってみましょう。図４をご覧ください。

図４

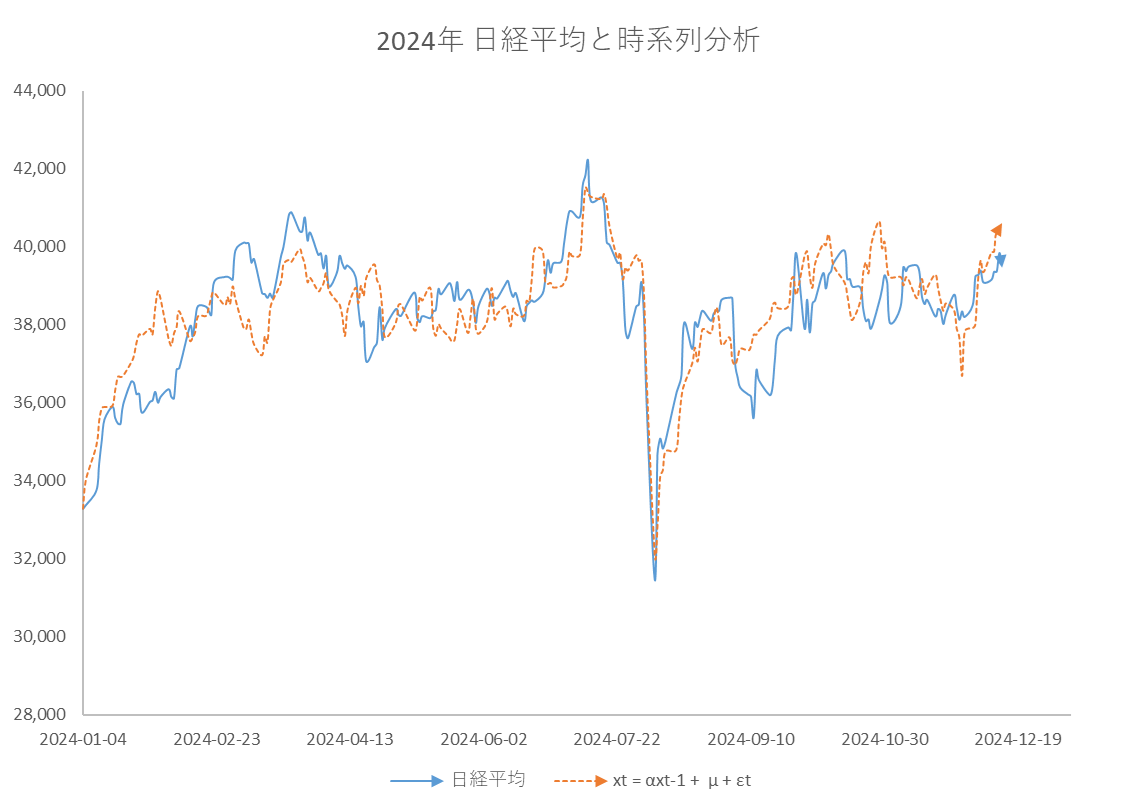
青の実線が日経平均の推移、オレンジの破線が式（１）において初期値 x₀＝33,288（2024年1月4日の終値）、α=0.9、μ=3,900、ノイズ（ε)を平均 0, 標準偏差400の確率正規分布としたときの一例（2024年8月1日、2日、5日に対前日比-2.0%、-5.4%、-12.3%のノイズを入れた。）

 

おおよそ再現できています。となると、世の中の急落現象を時系列分析したとき、それらのパラメーターを集めていくとそこにはある一定の法則があるのではないか？という気がしてきます。たとえば、自然がなぜか地球の重力加速度を 9.8m/s² に設定しているように、社会もある一定のパラメーターで動いている可能性はないでしょうか？

つづく

記事一覧へ戻る