数理経営のすすめ – その2「ゆらぎ」で、経営環境の絶えまない変化や、経営者の迷いなど、内外から受けるゆらぎの度合いが大きくなればなるほど成長が削がれてしまうことを、数式と計算によって示しました。これまで経験的、感覚的感じていたことが、数理的に裏付けられたことで、より納得感が増してすっきりしたのではないでしょうか。

さて、ここまで一社の成長だけをみてきましたが、ここからは複数社の成長をみていきます。同業者との競争、アウトソーシング、異業種間の共創、オープンイノベーションなど、企業の成長はそれをとりまく企業との関係においてさまざまな影響を受けます。

さて、突然ですが、これまで次ようなことを聞いたり、経験したりしたことはありませんか？

１）競争相手が現われると成長が鈍化する。

２）自社にない経営資源を他社に求めると（そうでない場合に比べて）より成長する。

３）同異業者が集まると（そうでない場合に比べて）クラスター効果でより成長できる。

４）来年度の予算（売上や利益目標）を提出すると、毎年「上方修正」を求められる。

 

ここでは以上のようなことがなぜ起こるのかという理由を数理的に究明します。

 

まずは、シンプルに「ゆらぎ」のない場合からはじめましょう。

x 社とy 社の基本行動パターンをそれぞれ、

$$\frac{dx}{dt}=r_{1}x(1+\frac{x}{K_{1}})\tag{1}$$

$$\frac{dy}{dt}=r_{2}y(1+\frac{y}{K_{2}})\tag{2}$$

とします。これらは、その1「成長」でみた経営者目線を取り込んだ数式で、その成長曲線は上限のあるS字形になります。ここで、r₁ 、r₂ は成長係数 、K₁ 、K₂ が 経営者目線です。

次に x 社と y 社が競争相手として絶えずしのぎを削っているとします。y 社が x 社に影響を与える度合いを a(>0)、x 社が y 社に影響を与える度合いを b(>0) 、（以下これらを競争係数とよびます）とすると、式 (1) と (2) は以下のようになります。

$$\frac{dx}{dt}=r_{1}x(1+\frac{x}{K_{1}})-axy\tag{3}$$

$$\frac{dy}{dt}=r_{2}x(1+\frac{y}{K_{2}})-bxy\tag{4}$$

「成長＝売上」ととらえて、x 社の売上と y 社の売上の初期値とその組み合わせを以下の四通りとします。① は x と y が同時期に事業を開始した場合、② は x が先行している場合、③ は y が先行している場合、④ は両社がほぼ同じ売上規模である場合、ととらえます。

表1

売上	①	②	③	④
x 社の初期値	1	90	1	90
y 社の初期値	1	1	90	90

 

式 (3)、(4) に代入するそれぞれの係数は以下のとおりとします。

表2

	成長係数 (r)	経営者目線 (K)	競争係数 (a,b)
x 社	0.2	80	0.0010
y 社	0.3	70	0.0015

 

これで計算に必要なすべての係数がそろいましたので、四つの組み合わせがその後どう変化するかを計算できます。方法は 成長 – Excel と同じです。計算結果を横軸に x 社の売上、縦軸に y 社の売上をとる散布図に展開すると図 1 のようになります。

図1

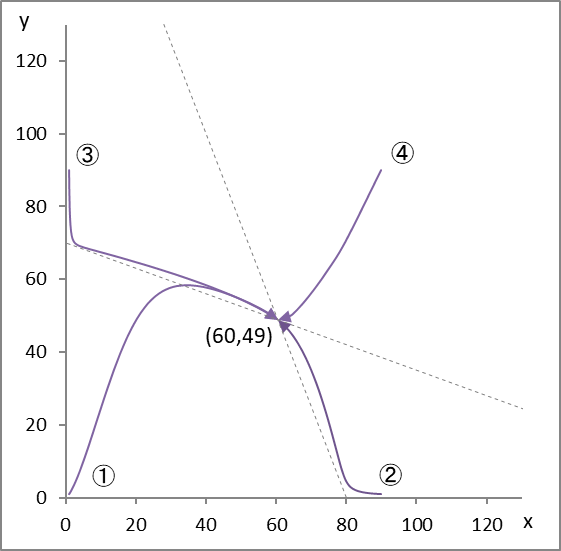
r₁=0.2, r₂=0.3, K₁=80, K₂=70, a=0.001, b=0.0015, 平衡点 (x,y) = (60,49)

グレーの破線はアイソクラインと呼ばれる境界線。x と y の増減と減少の組み合わせがここで切り替わる。

 

興味深いことに、初期値が違っていても時間の経過とともに平衡点に向かいます。そして、一旦平衡点に到達するとそれ以降、いくら時間が経過してもそこにとどまります。平衡点の座標は (60,48) ですから、経営者目線 (K₁) が 80 の x 社の売上は 60に、経営者目線 (K₂) が 70 の y 社の売上は 48 にとどまります。これが、先に述べた、「競争相手が現われると成長が鈍化する」という経験則の数理的裏付けです。

平衡点を競争のないときの経営者目線にもどすためには、両社はさらに目線を上げる必要があります。図2をご覧ください。もし、平衡点の座標を (80,70) に戻したいのであれば、新たな経営者目線は、x 社が 124、y 社は 118 でなけれなりません。経営者が毎回、予算の上方修正を求める理由がここにあります。

図2

r₁=0.2, r₂=0.3, K₁=124, K₂=118, a=0.001, b=0.0015, 平衡点 (x,y) = (80.2,70.7)

グレーの破線はアイソクラインと呼ばれる境界線。x と y の増減と減少の組み合わせがここで切り替わる。

競争相手がいる場合は経営者目線をより上げないと、目標の売上に到達しない。

 

では、反対に x 社と y 社が、たとえばオープン・イノベーションのような共創関係にある場合を考えます。式 (3) と (4) の競争係数の符号をマイナスからプラスに変更するだけでよいので、

$$\frac{dx}{dt}=r_{1}x(1+\frac{x}{K_{1}})+axy\tag{5}$$

$$\frac{dy}{dt}=r_{2}x(1+\frac{y}{K_{1}})+bxy\tag{6}$$

となります。

 

さあ、このとき、x 社と y 社の成長はどのように変化するでしょうか。係数はすべて表1 と表2 と同じで、競争係数の符号だけが違います。 図3 が計算結果です。平衡点が（126, 114）へ移動しています。

図3

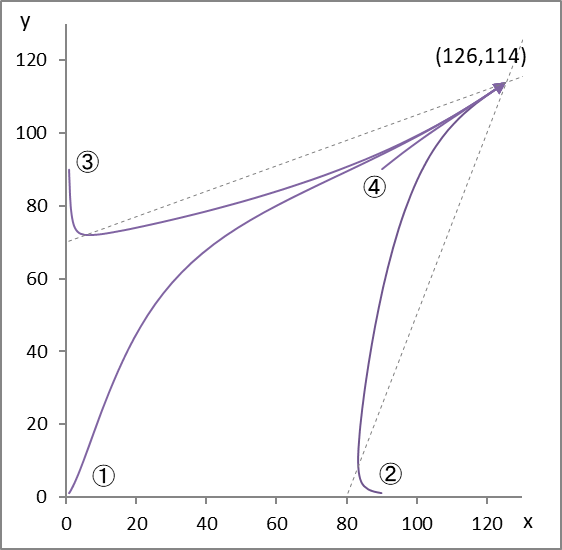
r₁=0.2, r₂=0.3, K₁=124, K₂=118, a=0.001, b=0.0015, 平衡点 (x,y) = (126,114)

グレーの破線はアイソクラインと呼ばれる境界線。x と y の増減と減少の組み合わせここで切り替わる。

二社が共創関係にあると単独での成長限界を超えて成長することができる。

 

二社が共創関係にあると、単独での成長限界（＝経営者目線）を超えて成長できることがわかります。これが、自社にない経営資源を他社に求めることでより成長できる数理的証明です。

異業種が交流することで、新しい発想が産まれたり、地理的に集結することでブランド力や集客力が産まれたりして成長が底上げされるのがクラスター効果です。これは、二社の共創である式 (5) と (6) を三社、四社、・・・と増やしていくことを意味します。たとえ係数がわずかな値であっても、各社の売上は、ちりも積もればで、少しずつ大きくなっていきます。

アイソクライン（境界線）や平衡点の計算方法などにご興味がある方は、競争と共創 – Excel をご覧ください。

数理経営のすすめ、その4 では、「クラスター効果」をもう少し掘り下げてみますのでお楽しみに！

 

＜追記＞

つづきは、2021年6月29日付のブログ をご覧ください。

 

 

 

 

 

 

記事一覧へ戻る