経営は「経験と勘?」 いや、「ビジョンと戦略?」 どちらも否定はできませんが、「数値化」されていないところは共通しています。物体の運動はニュートンの運動方程式によって数式で表現できますし、コロナ・ウィルス感染者数も数理モデルによって予測計算することができます。我々自身の健康もあらゆる指標を数値化し、その変化を辿ることで今後の健康状態を予測し、疾病を防止することができる時代になっています。
自然科学の理論は必ず実験や観測によってその正しさが証明されています。逆に自然現象をうまく説明するために理論が構築されているという言い方もできます。であれば、社会現象を数理的にうまく説明するための理論もつくれるのではないでしょうか。本日のテーマは「成長」です。
成長
経営者Aは、現在の売上 $x_{0}$を毎年、同額の$a$ だけ伸ばすと決めて、それを実現するとします。仮に、初期の売上 $x$ をゼロとし、その後の増加額 $a$ を $1$ とすると、任意の時間 $t$ が経過したときの売上は図1 のように直線になります。
図1
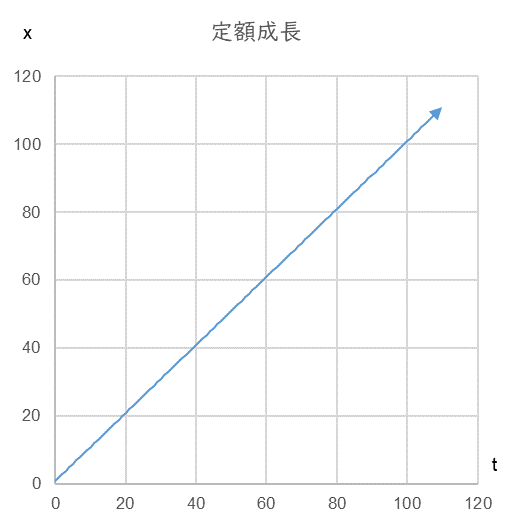
売上 x(単位は任意)が一定の額 a で増えるときの売上の時系列変化。未来の売上はこの直線上にあります(横軸は任意の時間)。
売上が一直線に増える続けるわけですから順調な事業のようにみえます。しかし図2をご覧ください。売上の対前年増加率のグラフです。時間の経過とともに低下しています。「定額」成長する売上の変化率は「右下がり(下に凸)の曲線」になります。
図2
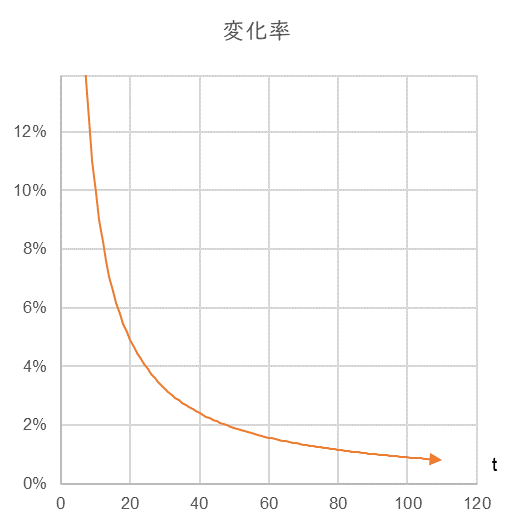
定額成長する売上 x の変化率 の時系列変化(横軸は任意の時間)。売上の変化率は右下がり(下に凸)の曲線となりいつまでも低下し続けます。
では、初期値 $x_{0}=1.0$ で、単位時間あたり 5% の変化率で成長する事業の売上はどうなるでしょうか。図3をご覧ください。右上がりの下に凸の曲線になります。
図3

単位時間あたりの変化率が 5% の場合の売上 x の時系列変化。未来の売上はこの右上がり(下に凸)の曲線上にあります。
一方、変化率は 5% で一定なので、水平な直線になります(図4)。
図4
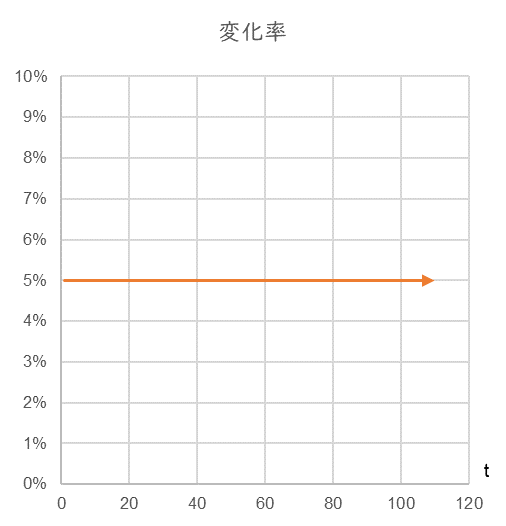
さて、定額であれ定率であれ一定の成長を続けるためには、まず経営者がそう思い続けることが必要です。その思いはいかなる「瞬間」においてもゆらぎないものでなくてはなりません。それがその経営者の「基本行動パターン」を形成します。ここでその瞬間瞬間の基本行動パターンを $\frac{dx}{dt}$ と表します。これは分数ではなく「記号」ですので、上から「ディーエックス・ディーティー」と読んでください。
定額成長の場合は、直前の売上(前月でも前年でも単位は何でも構いません)に関わらず、毎回同額の $α$(単位は任意)だけ増やすという基本行動パターンですので、
$$\frac{dx}{dt}=α\tag{1}$$
です。仮に、初年度の売上 $x_{0}$ をゼロ、目指す定額増分 $α$ を 1 とすると、時間 $t$ と売上 $x$ の関係は表1 のようになります。
表1
| 時間 $t$ | 売上$x$(図1) | 売上 $x$ の変化率(図2) | $$\frac{dx}{dt}=α$$ |
| 0 | 0 | ||
| 1 | 1 | 100.0% | 1 |
| 2 | 2 | 50.0% | 1 |
| 3 | 3 | 33.3% | 1 |
| 4 | 4 | 25.0% | 1 |
| 5 | 5 | 20.0% | 1 |
| 6 | 6 | 16.7% | 1 |
| 7 | 7 | 14.3% | 1 |
| 8 | 8 | 12.5% | 1 |
一方、定率成長の場合は、経営者は直近の売上 $x$ を絶えず意識する必要があります。前年度の売上に目指す増加率($r$ とします)を掛け合わせた分だけ売上を伸ばす必要があるからです。よって、このときの基本行動パターンは、直近の売上 $x$ に $r$ を掛け合わせるので、
$$\frac{dx}{dt}=rx\tag{2}$$
と書けます。
仮に、初年度の売上 $x_{0}$ が $1$ 、$r$ が $0.05$ のとき、時間 $t$と売上 $x$ の関係は表2のようになります。初年度の売上 $1.0$ に $0.05$ をかけた $0.05$ が次年度に達成すべき増分です。よって、次年度に目指すべき売上は $1.0+0.05=1.05$ です。同様に、三年度は、次年度の売上 $1.05$ に $0.05$ を掛けた $0.053$ を増やす必要があるので、目指すべき売上は $1.05+0.053=1.103$ となります。
表2
| 時間 $t$ | 売上 $x$ (図3) | 売上 $x$の変化率(図4) | $$\frac{dx}{dt}=rx$$ |
| 0 | 1.000 | ||
| 1 | 1.050 | 5.0% | 0.050 |
| 2 | 1.103 | 5.0% | 0.053 |
| 3 | 1.158 | 5.0% | 0.055 |
| 4 | 1.216 | 5.0% | 0.058 |
| 5 | 1,276 | 5.0% | 0.061 |
| 6 | 1.340 | 5.0% | 0.064 |
| 7 | 1.407 | 5.0% | 0.067 |
| 8 | 1.477 | 5.0% | 0.070 |
さて、ここで定率成長のグラフ(図3)をもう一度ご覧ください。このままですと無限大に発散します。売上は市場規模そのものよりは大きくなりませんし、市場占有率にも限界がありますから、どの経営者にも多かれ少なかれ潜在意識の中に「上限」が存在するのではないでしょうか。よって、この無意識の「上限」を基本行動パターンの $\frac{dx}{dt}$ に組み込んでみましょう。
売上を $x$、上限を $K$ として、$1-\frac{x}{K}$ を考えます。$x$ が $K$ に近づけば近づくほど $1-\frac{x}{K}$ はゼロに近づきますから、徐々に成長が鈍化するはずです。よって、式(2)にこの $1-\frac{x}{K}$ を掛け合わせてみましょう。
$$\frac{dx}{dt}=rx(1-\frac{x}{K})\tag{3}$$
このとき、時間 $t$ と売上 $x$ の関係は、表2の $\frac{dx}{dt}=rx$ を 式 $(3)$ に置き換えればいい(=基本行動パターンが変わる)ので、以下のようになります。
表3
| $t$ | $x$ | $x$ の変化率 | $$\frac{dx}{dt}=rx(1-\frac{x}{K})$$ |
| 0 | 1.000 | ||
| 1 | 1.050 | 4.950% | 0.050 |
| 2 | 1.103 | 4.948% | 0.052 |
| 3 | 1.158 | 4.945% | 0.054 |
| ・ | ・ | ・ | ・ |
| ・ | ・ | ・ | ・ |
| 198 | 99.515 | 0.026% | 0.025 |
| 199 | 99.539 | 0.024% | 0.024 |
| 200 | 99.562 | 0.023% | 0.023 |
r=0.05, K=100 としたときの x とその変化率の時系列推移
グラフにすると、図5 の実線のようになります。無限大に発散する定率成長(破線)から上限のある曲線(S字カーブ)に変わりました。
図5
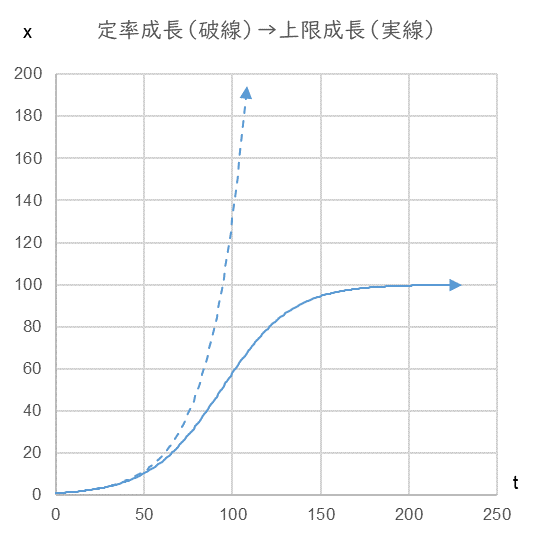
この「S字カーブ」は耐久消費財の普及率によく現れます。
図6
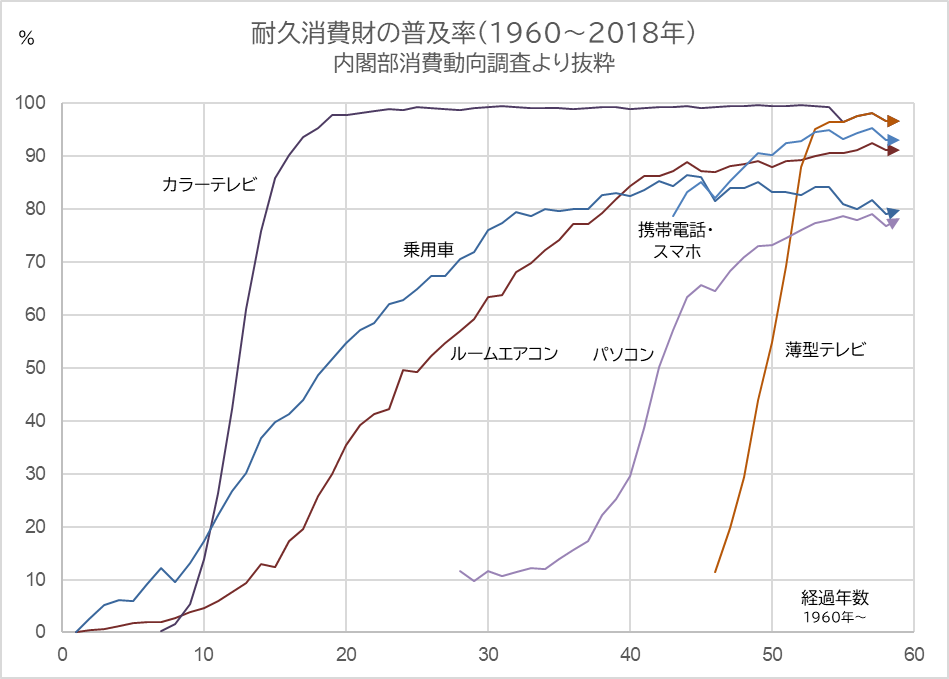
生活必需品になればなるほど成長係数の r の値が大きくなり成長曲線の勾配が急になります。
さて、経営者が「上限」に到達したことを良しとしてしまうと、事業はそれ以上大きくなりません。会社はよく「経営者の器以上に大きくならない。」と言われます。その「経営者の器」、または「目線の高さ」が式 $(3)$ の $K$ です。
売上の成長が鈍化したときに経営者が目線を上げることができるかできないかはその後の結果に大きな影響を与えます。図7をみてください。青の破線は $K=100$ のときの成長曲線、緑の実線が $t=50~100$ の間に $K$ を $100$ から$200$ へ上げたときの成長曲線です。
図7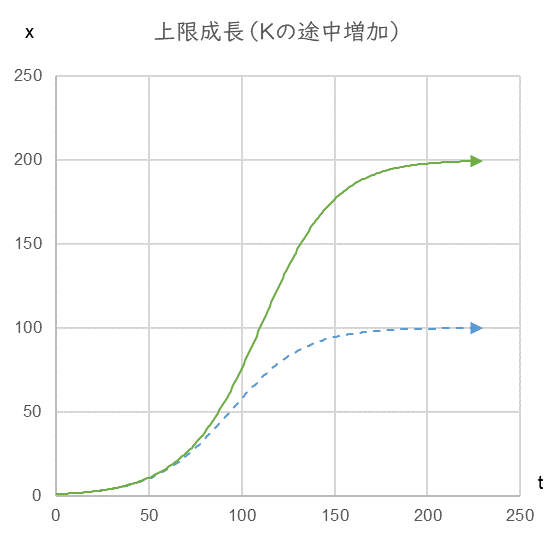
一方、ひとつの事業が上限に達したときに、もうひとつの事業を積み上げるという方法もあります。図8は $K=100$ の事業(青色)が上限に達したときに、もうひとつの $K=100$ の事業(緑色)を積み上げたときの成長曲線です。
図8

このとき、変化率は図9のように推移しています。
図9
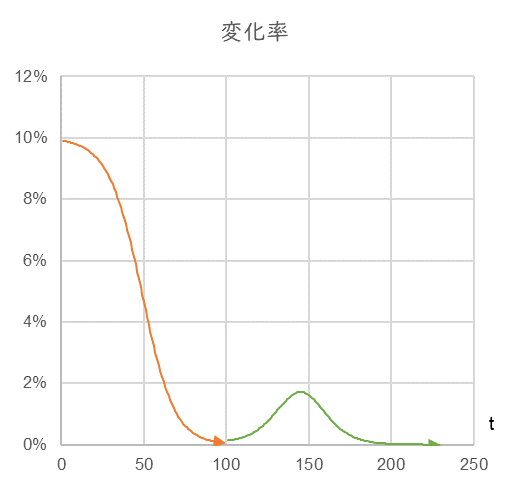
図9 は時間経過とともに下がり続けた変化率が、新たな事業を積み上げることでプラスに反転することを示しています。但し、追加した事業もその上限に近づくとまた成長がとまります。つまり、変化率がまたゼロに近づいてしまいますから、絶えず成長するためには「変化率の変化」に注目して早め早めに手を打つ必要があることが分ります。実際、図8において、$K$ を階段状に上げていくと成長曲線はどう変化するでしょうか。
図10
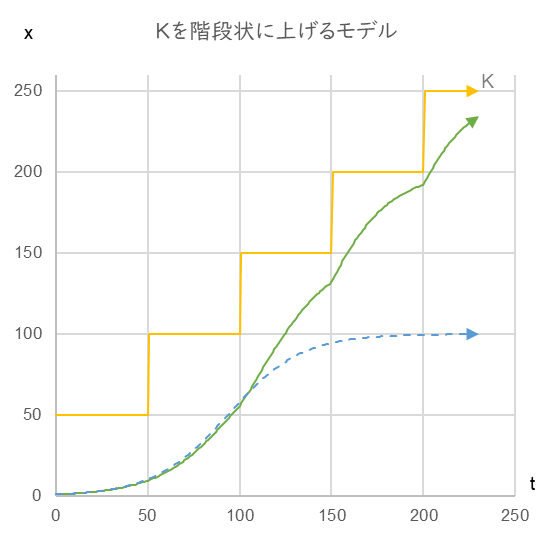
r=0.05, K を 50 → 100 → 150 → 200 → 250 と階段状に上げたときの成長曲線(緑の実線)
図10の緑の実線が、上限に甘んじることなく絶えず目線をあげたときに達成される成長曲線です。このとき、変化率は以下のように推移しています。
図11

図10 の成長曲線の変化率の推移
絶えず目線を上げて経営するということは、単純にいえば売上を時間の経過とともに上げていこうとする行動パターンですから、式 $(3)$ を以下のように変更してみましょう。
$$\frac{dx}{dt}=at+b\tag{4}$$
図12と図13の青色の実線はセブンイレブンとトヨタ自動車の売上推移です。緑色が式 (4) で描いた曲線ですが、実際の売上をよく近似できていることが分ります。
図12 図13

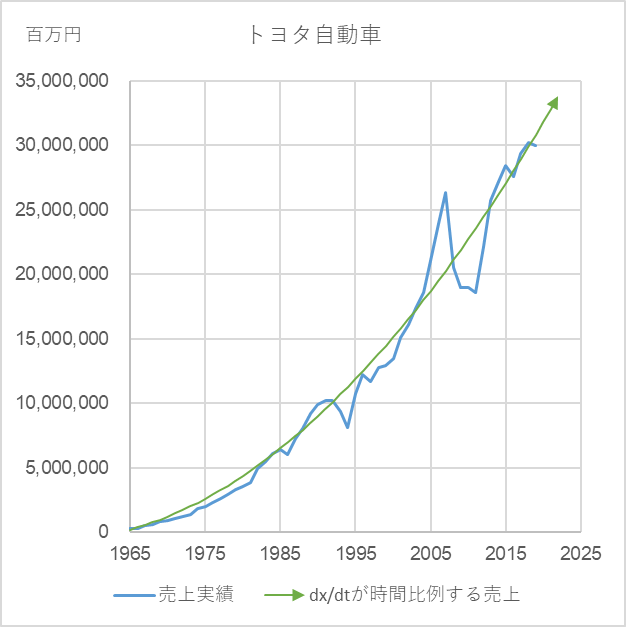
a=50, b=7 a=14,800, b=160,000
セブンイレブン: 元データ 売上高、店舗数推移|セブン-イレブン~近くて便利~ (sei.co.jp)
トヨタ自動車:元データ http://www.toyota.co.jp/jpn/company/history/75years/common/pdf/financialstatement_of_income.pdf
さて、ここまで「目線を上げる」ことを強調してきましたが、一方で、市場規模自体が縮小することもあります。$K$ を減少する市場規模と捉えて、式 $(3)$ の $K$ を式 $(4)$ に変更してみましょう。
$$\frac{dK}{dt}=\frac{a}{\sqrt{t}}\tag{4}$$
これを式 $(3)$ の $K$ と入れ替えると、
$$\frac{dx}{dt}=rx(1-\frac{x}{\frac{dK}{dt}})\tag{5}$$
となります。図14の緑の実線をご覧ください。確かにピークに達したあとは右肩下がりになっています。
図14

r=0.05, a=1.0, dK/dt}=a/√t のときの成長曲線(緑の実線。青の破線は K=100 (一定)のときの成長曲線)
試しに、式 (5) を平均身長と平均体重の年齢別推移にフィッティングすると以下のようになります。
図15 図16
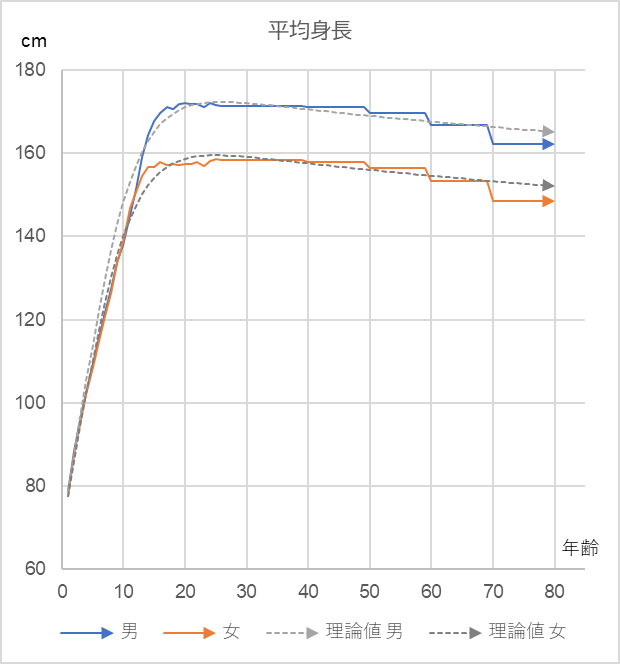

元データ:国民健康・栄養調査(厚労省 2019年)
身長(男):r=0.2, a=0.2, K0=181
体重(男):r=0.2, a=1.0, K0=80
身長(女):r=0.2, a=0.2, K0=172
体重(女):r=0.23, a=0.9, K0=64
以上、いろいろな成長曲線をみてきましたが、これらのモデルは成長の本質的な特長をつかんでいるため応用範囲が広いです。手元にあるデータを是非、式 $(1)$ ~ $(5)$ を使ってグラフにしてみてください。表2 や 表3 の要領でエクセルに展開すればすぐに描けます。きっとおもしろい発見があるはずです!
図1~16 、表1~3 のエクセル版はこちらから 👉 成長 – Excel
<追記>
つづきは、2021年5月31日づけのブログ をご覧ください。
記事一覧へ戻る