S&P500の未来予測を確率微分方程式で行う方法
はじめに
確率微分方程式の解を株価に見立てることによってその将来の動きを確率的に予測することができます。ここでは米国の代表的な株価指数であるS&P500をとりあげます(以下、単純に株価と呼びます)。同方程式に含まれるパラメーターの値を探索したうえで、誰でも表計算ソフト(エクセル)で予測を体感できるようにしました。2020年3月にコロナ・ウィルスの世界的蔓延とともに発生した株価の暴落は投資家にとって最大の関心事と思われますが、1987年のブラック・マンデーや2008年のリーマン・ショック後の株価の回復を参考にしながら、具体的な計算を行い「いつ暴落前のレベルに戻るのか?」を探ります。
確率微分方程式のパラメーターの探索
確率微分方程式①とその解析解②には成長係数の $r$ とゆらぎ係数の $v$のふたつのパラメーターが含まれます(式 (1) から式 (2) への導出は、2023年1月23日付ブログをご覧ください)。$B(t)$ は株価のランダムな動き(平均ゼロ、標準偏差 1.0の標準正規分布に従うBrown運動)示すものとします。
$$\frac{dx}{dt}=rx+vx\frac{dB(t)}{dt} \tag{1}$$
$$x_{n}=x_{0}\ e^{(r-\frac{v^2}{2})t+vB(t)} \tag{2}$$
($2$) 式の $x_{0}$ は初期値です。解析解 $x_{n}$ は $x_{0}\ e{(r-\frac{v^2}{2})}$ を中央値としてゆらぐことが分かります(以後、この中央値のことを $µ$ と呼びます)。株価がこの解析解のひとつであると仮定し、ゆらぎ項 $vB(t)$ を無視して、初期値 $x_{0}$ = 16.66 (1950年1月3日の終値))が単純に 16,348日後に 2058.90 (2014年12月31日の取引の終値))に指数増加したと考えます。
$$(r-\frac{v^2}{2}) = r’$$
とおいて、($2$)式を
$$x_{n} = x_{0}\ e^{r’t}$$
とし、ここに初期値 $x_{0}$ と $x_{16348}$ の値を代入すると、
$${x = 16.66\ e^{r’*16348} = 2,058.90} \tag{3}$$
($3$)式より 、
$${r’ = 2.946×10^{-4}}$$
つまり、
$${r-\frac{v^2}{2} = 2.946×10^{-4}}$$
が得られます。
ここで、未知のパラメーターである $r$ と $v$ を探り当てる作業を行います。まず、株価の推移と $µ$ 線を横軸が経過日数、縦軸が対数のグラフにします。縦軸が対数であることより、中央値 $$µ=x_{0}\ e^{(r-\frac{v^2}{2})t}$$(オレジの線)は株価(水色の線)の初期値 $x_{0}$ と終値 $x_{16348}$ を結ぶ直線になります。
次に、$r$ と $v$ の組み合わせをランダムに設定して、実際の株価の動きと照らし合わせてみましょう。$µ$ からのゆらぎ $v$ の度合いは以下のように中央値に標準偏差 $v\sqrt{t}$ の倍数を掛け合わせることで表現できます。
$$x_{0}\ e^{(r-\frac{v^2}{2})t+v\sqrt{t}} \tag{+v}$$
$$x_{0}\ e^{(r-\frac{v^2}{2})t-v\sqrt{t}} \tag{-v}$$
$$x_{0}\ e^{(r-\frac{v^2}{2})t+2v\sqrt{t}} \tag{+2v}$$
$$x_{0}\ e^{(r-\frac{v^2}{2})t-2v\sqrt{t}} \tag{-2v}$$
図1のオレンジの直線が $µ$ 、彗星の尻尾のような四本の破線が株価がゆらぐ範囲を示しています。水色が実績値、紺色の線が任意に設定したパラメーターで計算したサンプル・パスです。
図1 r=0.0003, v=0.00329, r-v2/2=2.946×10-4
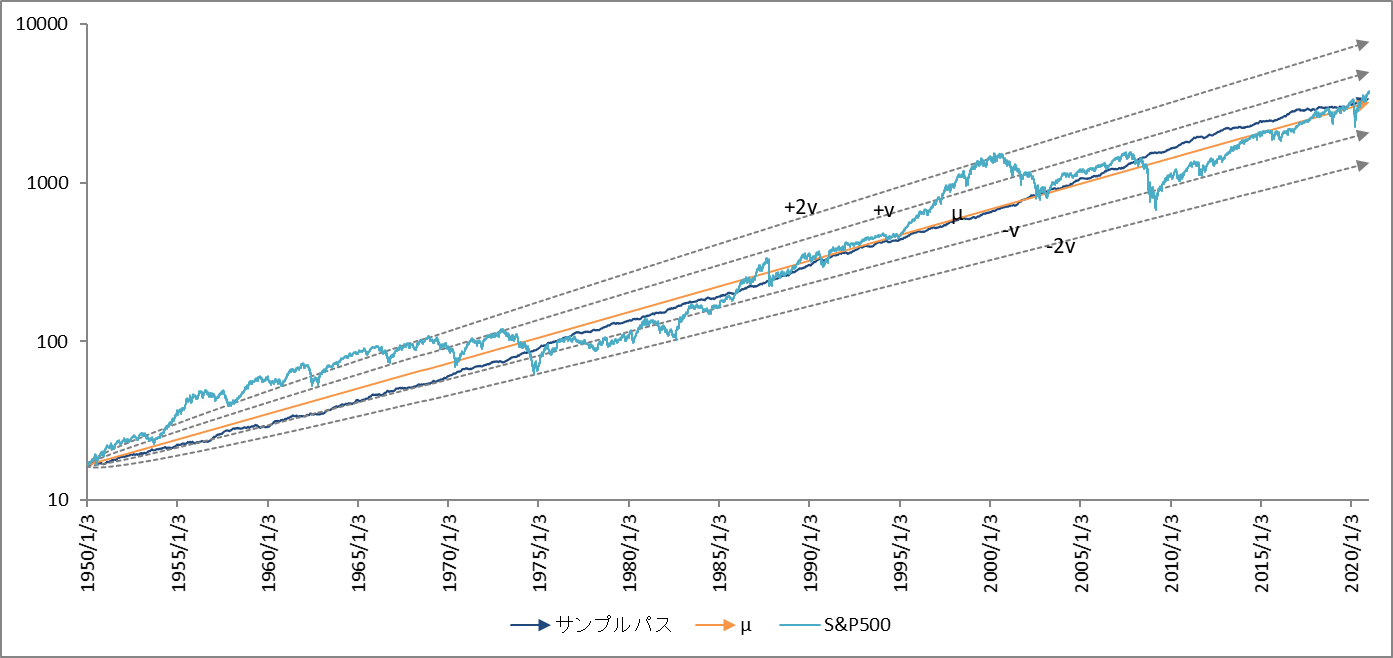
図2 r=0.0004, v=0.01452, r-v2/2=2.946×10-4
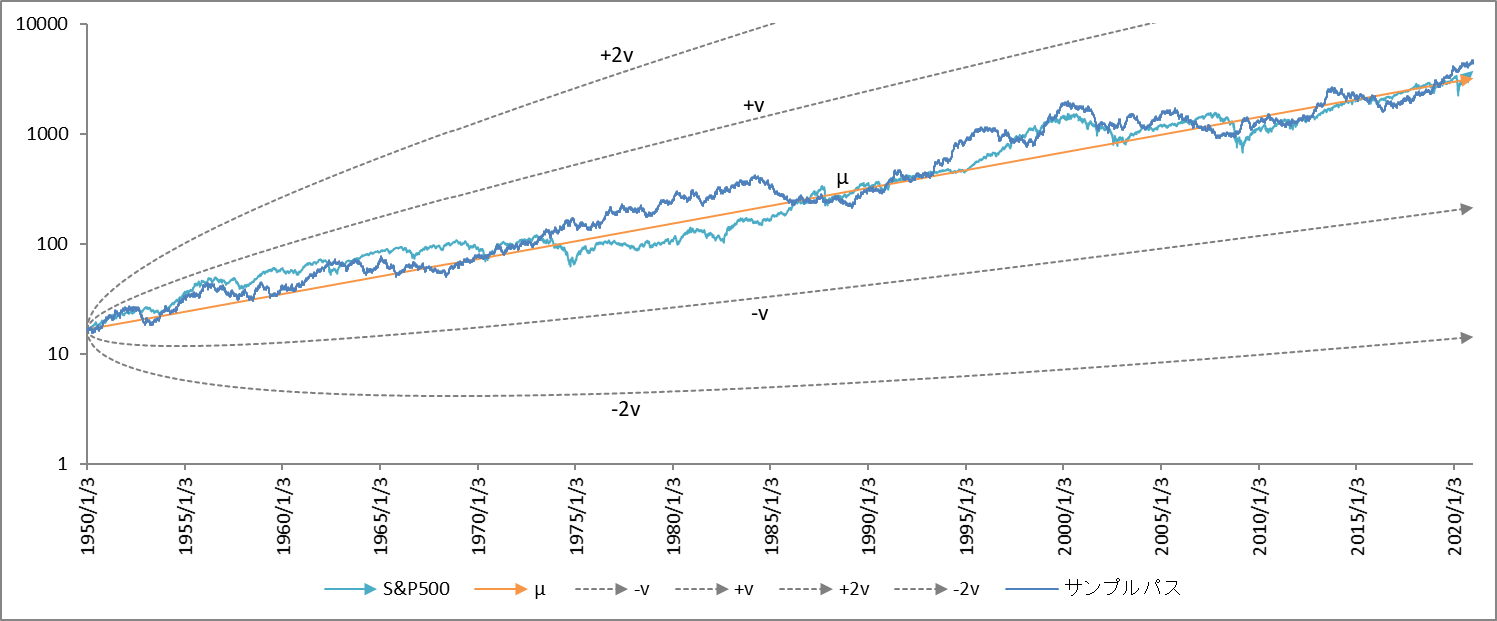
図3 r=0.0005, v=0.02027, r-v2/2=2.946×10-4
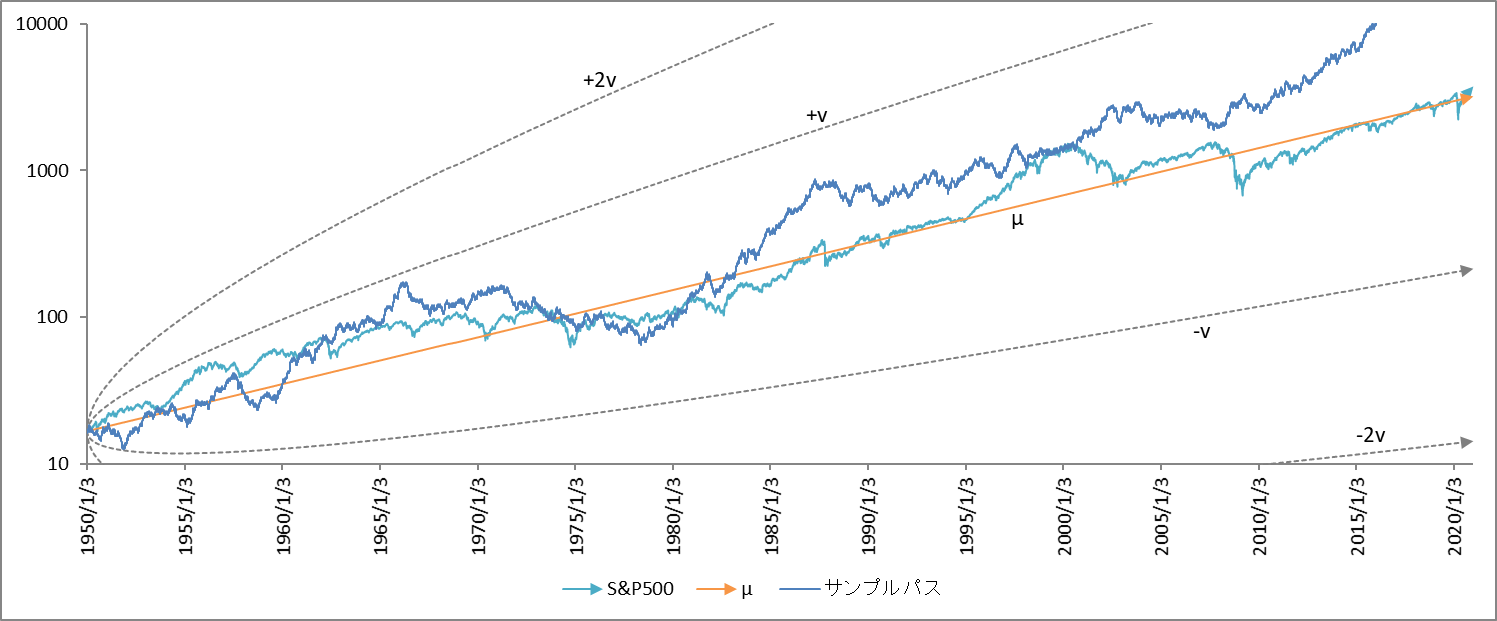
$v$ の値が大きくなるにつれてゆらぎ度合いが大きくなっていることが分かります。図1のサンプル・パス(紺色)は中央値 $µ$(オレンジ)にへばりついています、$v$ の値を大きくした図2、図3はサンプル・パスが $µ$ から少しずつ離れていくのが分かります。
このことを数値的に確認するために、それぞれのパラメーターの組み合わせにおける揺れ幅の度合いを測定してみましょう。
(A) $µ$ 線(オレンジ)と株価(水色)の差(二乗の平方根)を求める。
(B) 同様に、$µ$ 線とそれぞれのパラメーター($r$と$v$)で試算した値の差(二乗の平方根)を求める。
(C) (B) で求めた平方根の中で実際のかい離幅 (A)に近いパラメーターの組み合わせを探す。
実際にやってみた結果が、表1と表2 です。
表1 $r$ と $v$ の組み合わせ
|
|
a |
b |
c |
|
$r$ |
3.0 x 10-4 |
4.0 x 10-4 |
5.0 x 10-4 |
|
$v$ |
0.329 x 10-2 |
1.452 x 10-2 |
2.027 x 10-2 |
|
${r-\frac{v^2}{2}}$ |
2.946 x 10-4 |
2.946 x 10-4 |
2.946 x 10-4 |
${r-\frac{v^2}{2}}$ がわかっていますから、r を任意に選ぶと v は自ずと決まります。
表2 表1の組み合わせでそれぞれ100回計算したときに出現する値 (B) の出現回数
|
µとの乖離 |
a |
b |
c |
|
0~10,000 |
22 |
0 |
0 |
|
10,000~20,000 |
32 |
7 |
3 |
|
20,000~30,000 |
25 |
19 |
8 |
|
30,000~40,000 |
8 |
17 |
10 |
|
40,000~50,000 |
7 |
7 |
13 |
|
50,000~60,000 |
3 |
12 |
14 |
|
60,000~70,000 |
0 |
9 |
5 |
|
70,000~80,000 |
3 |
6 |
8 |
|
80,000~90,000 |
0 |
2 |
4 |
S&P500(実績値)の中央値 µ からの乖離を計算すると 20,000~30,000 の範囲にあります。一方、100回試行したときの最頻値が同範囲で出現するパラメーターの組み合わせは b です(aの最頻値は10,000~20,000、c の最頻値は40,000~60,000)。
この結果をもう一度、図1~図3と照合してください。
では、初期値 $x_{0}$=16.66 とパラメーターの組み合わせ b をそれぞれ($2$)式に代入すると、
$${x= 16.66\ e^{ 0.0002946t + 0.01452 B(t)}} \tag{5}$$
となります。残るは変化率 B(t) の数値化です。
表4の青の実線が、S&P500の1950年以降の対前日変化率の分布です。形状が正規分布に近いことがわかります。そこで、平均ゼロ、標準偏差 1.0 の正規分布(赤の破線)と、平均ゼロ、標準偏差 0.6(グレーの破線)と比較してみます。
図4
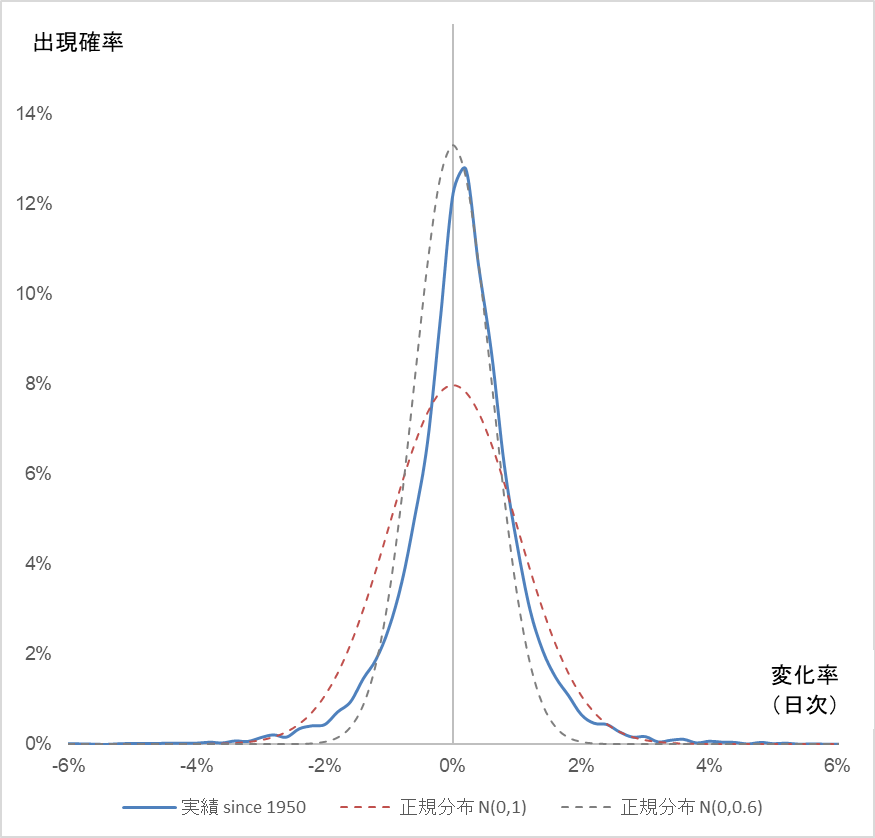
S&P500の変化率(対前日)と正規分布の比較
実績(青の実線)が標準偏差 1.0(赤の破線)の正規分布よりもスリムで、標準偏差 0.6(グレーの破線)により近いことがわかります。よって、予測に使用する変化率 は、エクセル関数を使って以下の様に定義します。
$$\frac{dB(t)}{dt} = NORMINV(RAND(),0,0.6)$$
$${B(t_{n}) = B(t_{n-1}) + \frac{dB(t_{n})}{dt}}$$
以上でブラウン運動項 $B(t)$ の数値化ができたので、あとはその値を($5$)式に代入すれば未来の株価を計算することができます。表3はその一例です。($B(t)$ は絶えず入れ替わりますので計算結果を記録したいときは「コピー → 形式を選択して貼り付け → 値貼り付け」としてください。)
表3 $t$ は 日数、$x$ が $t$ 日目の株価
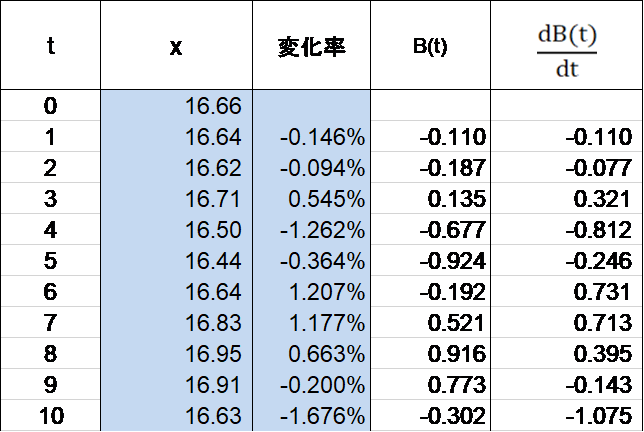
$B(t)$ によってさまざまな未来への道のりが産み出されますが、それらを「サンプル・バス」と呼びます。ではここで実際にコロナ・ショック後の株価がどう動くかシミュレートしてみましょう。初期値は2020年3月20日の2,304.92米ドル。確かに$\pm 2v$ 線の範囲内でゆらいでいるのが分かります(図4)。
図4 式($5$)で計算したサンプル・パス
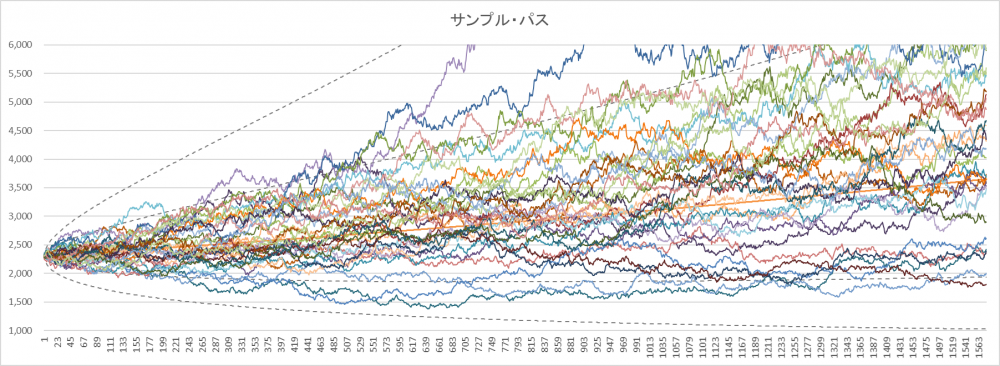
さて、次にこれら無数のサンプル・パスの中から未来の動きに近いのはどれか?を探り当てる方法を示します。
コロナ・ショックからの回復予測
2020年2月14日に史上最高値の3,380.16(終値ベース)を付けた株価はそれ以降不安定な動きを見せ始め、三月に入ると乱高下を繰り返し、同月末には最高値から30%近くも値を下げました(図5)。
図5
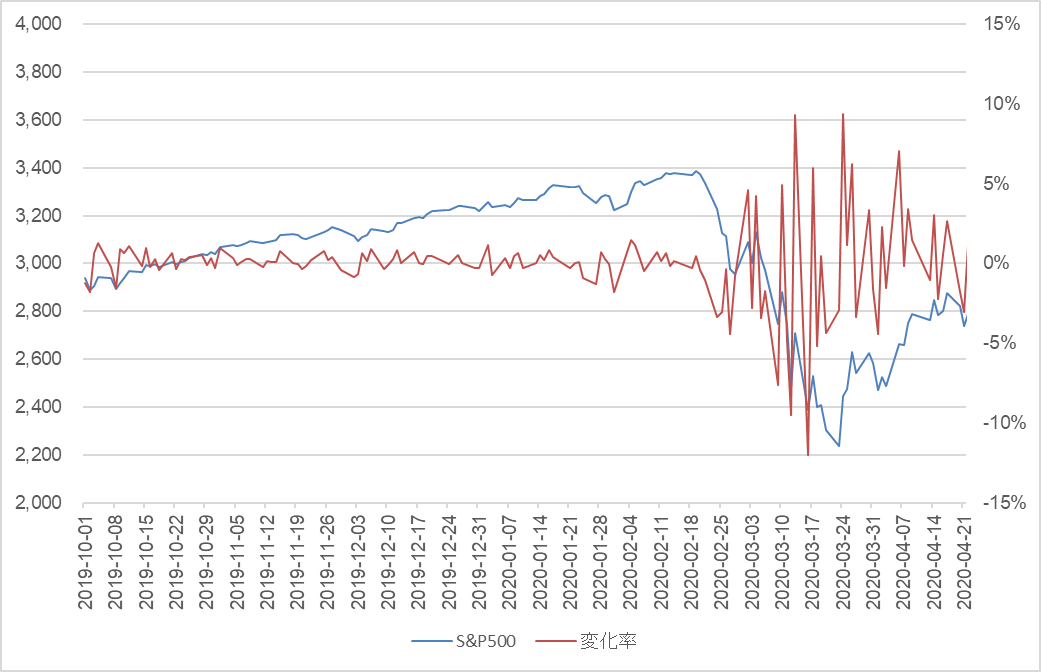
では、落ちた株価はいつ回復するでしょうか。表4は近年に発生した二回の暴落と今回の暴落の比較表です。下落率はリーマン・ショックの48.2%が最大でしたが、底値に到達するまでに210日を要しています。一方、ブラック・マンデーの下落率は31.5%でしたが、わずか二週間で底値に到達しました。2020年4月3日現在、コロナ・ショックの底値は、2020年3月23日の2,237.40で、下落率はブラック・マンデーを上回る33.9%、下落に要した日数は38日でブラック・マンデーに比べると下落スピードはやや緩やかですが、リーマン・ショックに比べると急激です。
表4
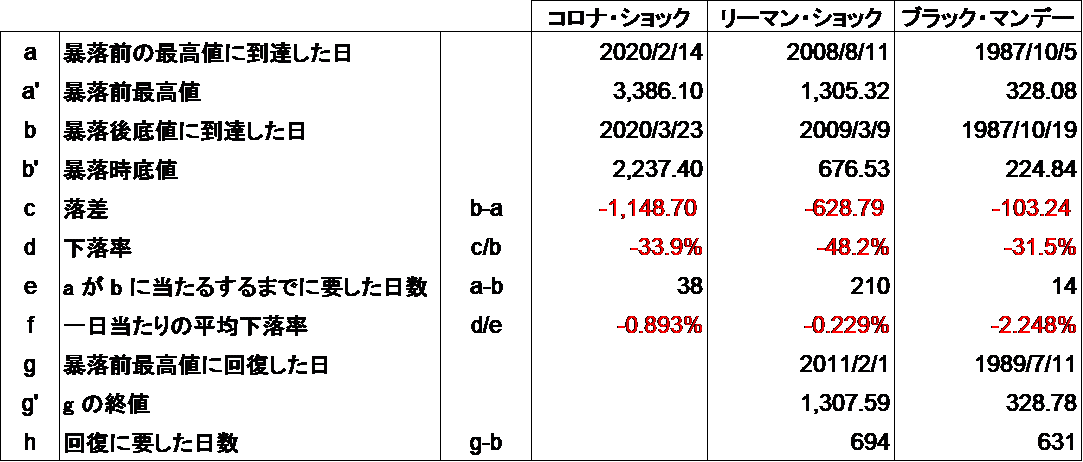
1987年のブラックマンデー後の動きを図6、2008年のリーマン・ショック後の動きを図7に示しました。ここで株価が「 $µ$ や $v$ 線に対してどの位置で回復したか?」に注目します。ブラック・マンデー(図6)では $µ$ 線と $+v$ の間、リーマン・ショック(図7)では $+v$ と $+2v$ の間で推移しています。
図6
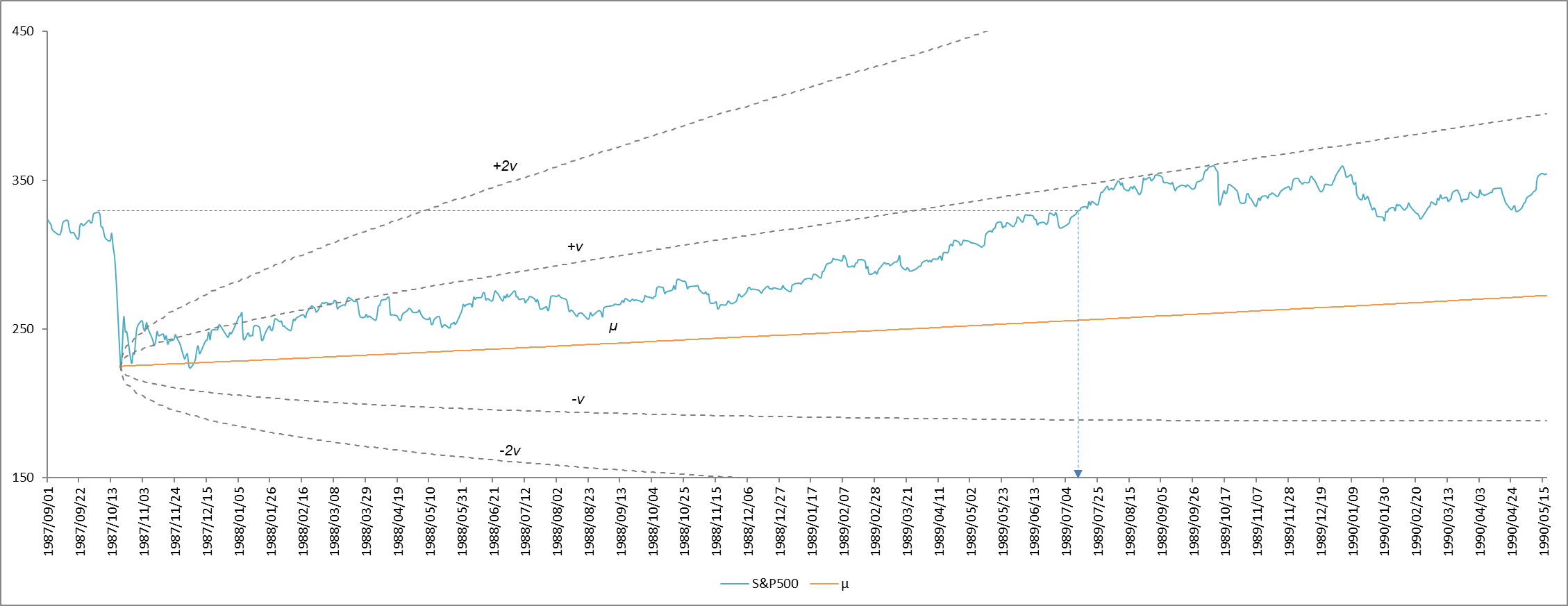
ブラックマンデー(1987年10月19日)からの回復。回復は概ね、µ と +v の間で行われ、 暴落前の最高値にもどるまでに要した日数は631日。
暴落前の最高値と暴落後の底値の落差31.5%。底値からは $µ$ と $+v$ の間で回復を続けています。
一方、リーマン・ショックはブラック・マンデーよりも下落率は大きく下落期間も長かったのですが、回復に要した時間はブラック・マンデーとさほど変わりませんでした。下落後、ブラック・マンデーが $+v$ 線上を推移した一方、リーマン・ショックでは $+2v$~$+v$ の間を動いています。
図7
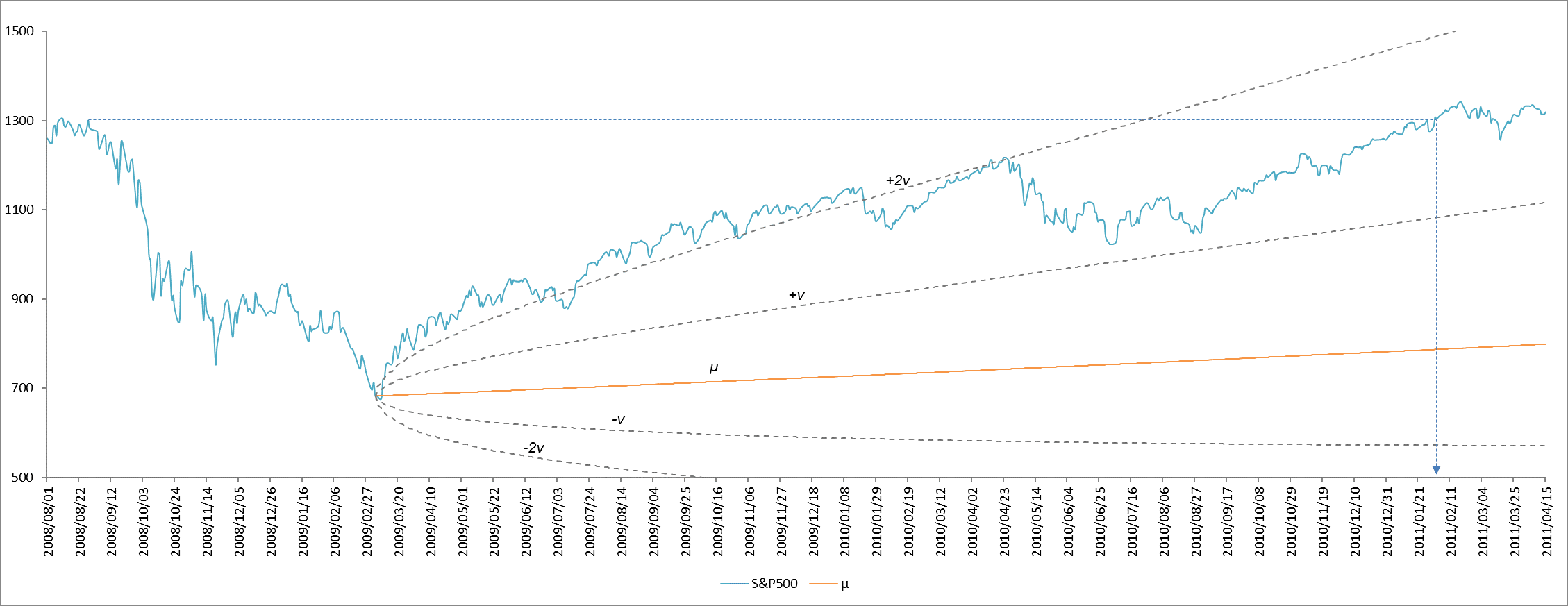
暴落前の最高値と暴落後の底値の落差48.2%。底値からは $+v$ と $+2v$ の間で回復しており、ブラック・マンデーを上回る回復力を示した。暴落前の最高値にもどるまでに要した日数は694日。
コロナ・ショックは今のところブラック・マンデーを若干上回る下落率であった一方で、下落のスピードはブラック・マンデーよりも緩やかであったことから、今後はおおよそ $µ$ 線と $+v$ 線の中間あたりを推移する可能性が高いと推察されます。よって、具体的には、図8より株価が暴落前の値に戻るのは一年後の2021年の2月から一年半後の10月あたりではないかと予測できます。
図8
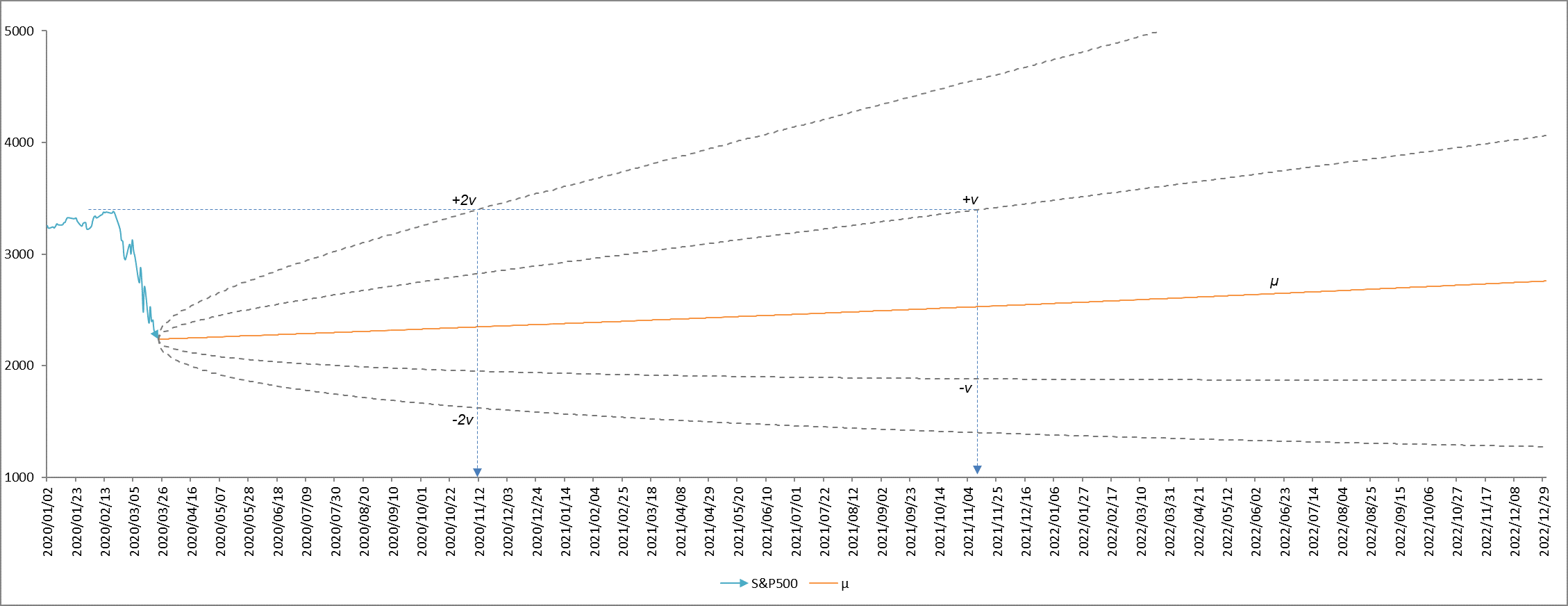
2021年3月23日現在のS&P500(終値)とその後の推移予測
暴落前の最高値から横軸に水平な線を引き、$+2v$、$+v$ 曲線と交わる点で、垂直におろした矢印の先が予測回復日です。
おわりに
コロナ・ショックがすでに底値に達しているのか、継続中なのかはいまの時点ではわかりません。リーマン・ショックは七か月間に二番底、三番底を経験しており、コロナ・ショック後も同じような推移を示す可能性もあります。底値、つまり初期値をどこにするかによって回復までの道のり( $µ$ 線と $v$ 線の間の動き)も変わりますが、予測方法は同じですので、ご興味のある方は付随のエクセル・テンプレートの初期値を適宜入れ替えて予測してみてください。
記事一覧へ戻る