これまで感染症やいろいろな社会現象を微分方程式で表してきましたが、今回は少し趣向を変えて自然現象の裏に隠れている数式についてみてみましょう。まず最初に取り上げるのが「よつ葉のクローバー」です。よつ葉のクローバーはなかなか見つかりませんが、どういうところで見つかり安いかご存知でしょうか？意外なのですが、ひとの足でよく踏みつけられるところなのだそうです。春から夏にかけて、「原基」という葉っぱの赤ちゃん状態が二～三日あり、そのときに外的損傷を受けると三つ葉になるはずだったクローバーがよつ葉になるのだそうです。時期的には6月～9月、まさにこれからの季節が見つかりやすいようです。（2019年6月22日にNHKで放送された「チコちゃんに叱られる」より。）

いきなりクローバーを描き出せる数式を見つけ出すのは無理ですので、まずは円からはじめます。単位円の方程式は、

$$x^2+y^2=1\tag{1}$$

でした。この数式をそのままグラフ描写ソフトの GeoGebra に書き込むと、以下のような円があらわれます。

図１

 

 

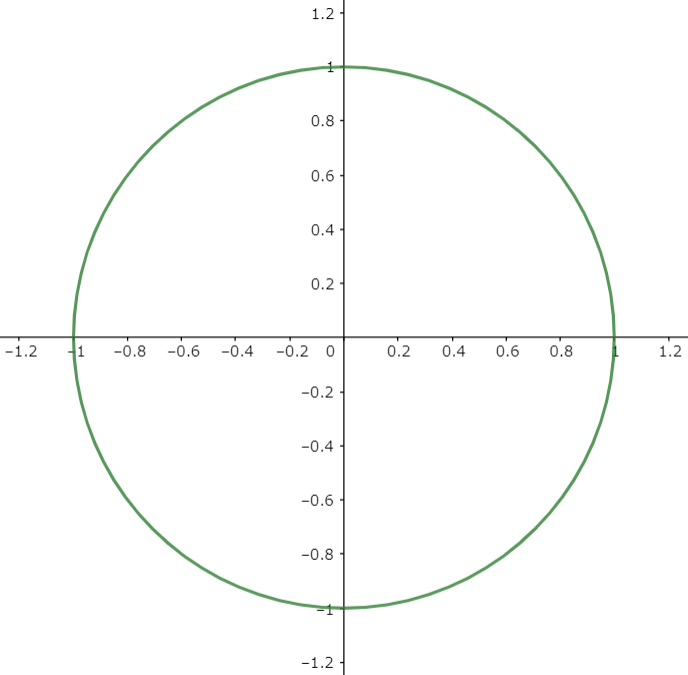
次に、円を一枚の葉っぱに見立てて、四つの式を組み合わせてみましょう。

$$x^2+y^2=x\tag{2a}$$

$$x^2+y^2=-x\tag{2b}$$

$$x^2+y^2=y\tag{2c}$$

$$x^2+y^2=-y\tag{2d}$$

図２

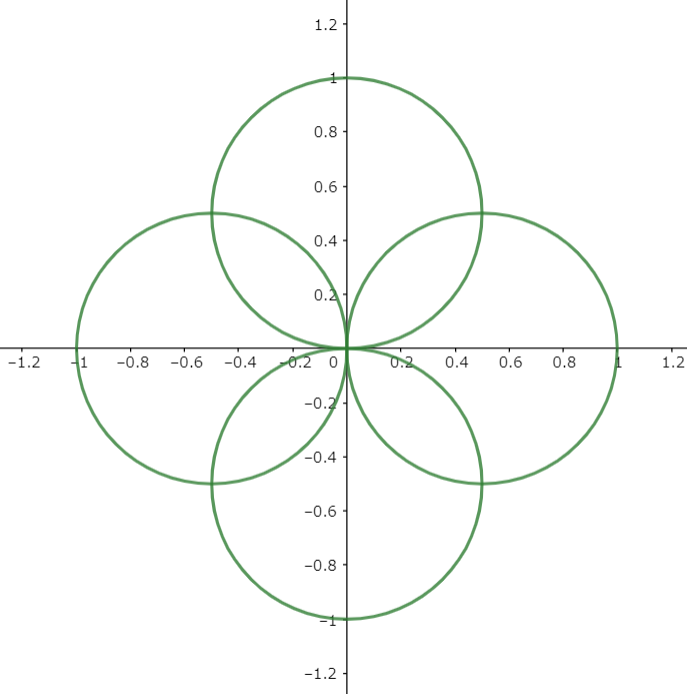
重なりもあってそれなりにいいのですが、形が円のままではクローバーらしくありません。それに数式が四つも必要です。

では、葉っぱの形をクローバーに近づけながら、数式も二つに減らします。

$$(x^2+y^2)^2=xy\tag{3a}$$

$$(x^2+y^2)^2=-xy\tag{3b}$$

図３

 

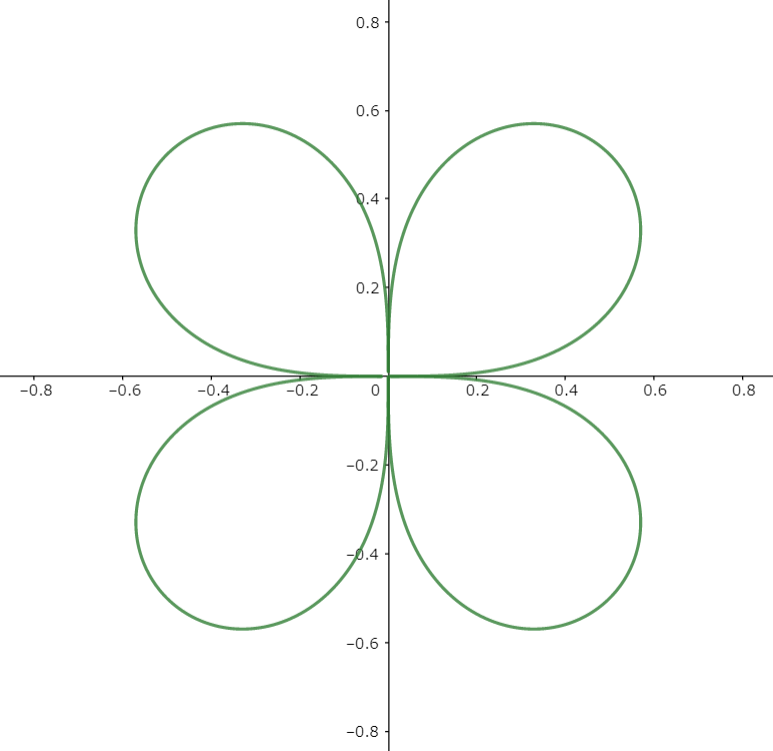
形がクローバーらしくなりました。重なりはなくなりましたが、使った数式はふたつだけです。ここまできたらやはり、数式を一本にまとめたくなります。

そこで、これです。

$$(x^2+y^2)^3=x^2y^2\tag{4}$$

図４

 

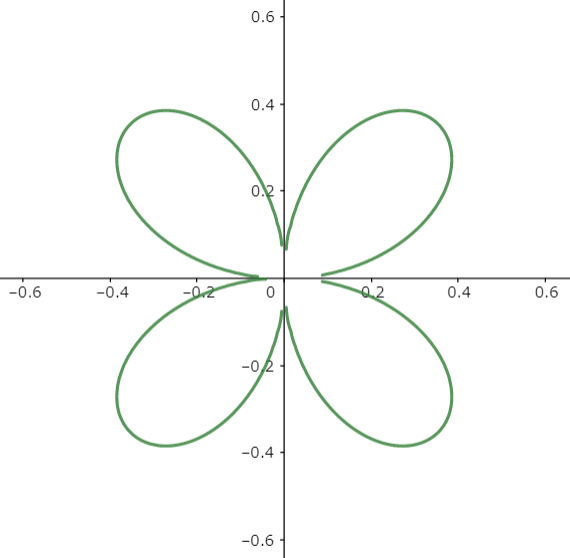
たったひとつの数式で「よつ葉のクローバー」が描けました！

少し、葉っぱが細長いので、もう少し自然に近づけてみましょう。

$$(x^2+y^2)^4=x^2y^2\tag{5}$$

図５

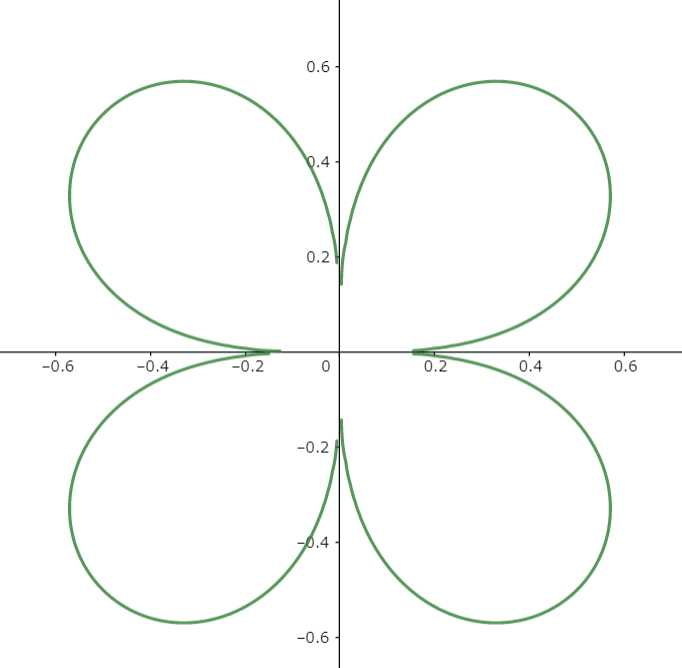
実際の写真と比べてみましょう。

図６

Free Photoサイト O-DAN より借用

 

なかなかいい感じに仕上がりました。

さて、クローバーの仲間には葉の形が「ハート型」になっているものがあります。

図７

Free Photo サイト O-DAN より借用 

 

これを描くには、まずハートマークを数式で表す必要があります。その極めて興味深い数式は 2022年6月17日付けのブログ、「ハートマーク」を一本の数式でかけるか？で紹介していますのでご覧ください。ここではその結果だけを借用します。

下のよっつの式を、GeoGebra に打ち込むと、

$$x^2+\left(1.3x-0.9-\sqrt{|y|}\right)^2=1\tag{5a}$$

$$x^2+\left(1.3x+0.9+\sqrt{|y|}\right)^2=1\tag{5b}$$

$$x^2+\left(1.4y-0.4-\sqrt{|y|}\right)^2=0.3\tag{5c}$$

$$x^2+\left(1.4y+0.4+\sqrt{|y|}\right)^2=0.3\tag{5d}$$

図８

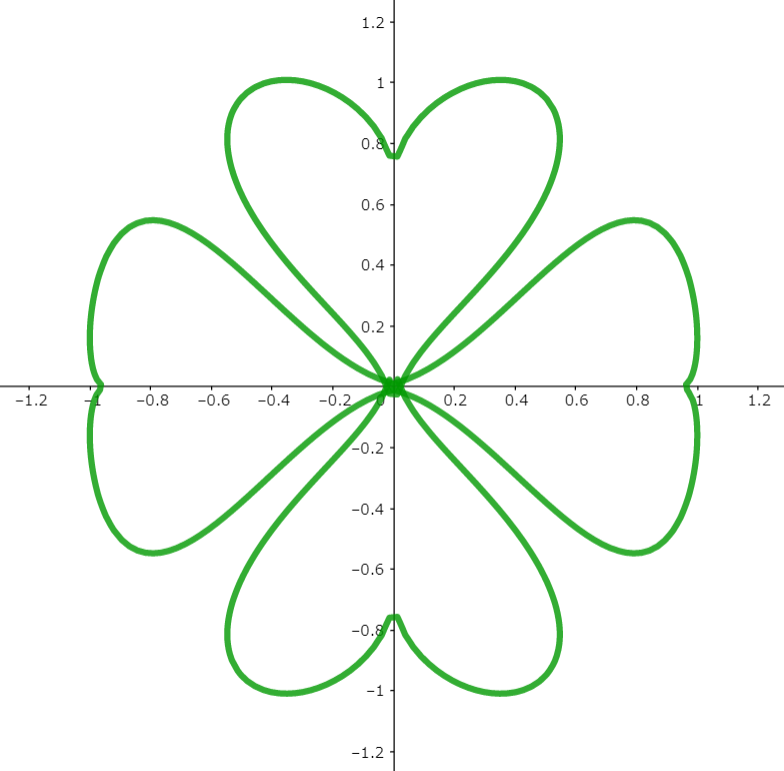
が現われます。確かにハート型になりました。

これが一本の数式で描けたらもっとすごいのですが・・・

 

おわり

 

＜参考文献＞

式 $(4)$ は、数学大図鑑（Newton Press, p64）を参照しました。

記事一覧へ戻る