ラプラスの「継起の規則」による成功確率の予測

2022年4月2日付けのブログで「次のプロジェクトが成功する確率」を計算しましたが、本日のテーマは「一敗の重み」です。

突然ですが、フランス革命の頃にラプラス（1749～1827）という数学者が、ベイズの定理から「継起の規則」（Laplace’s law of succession）を導きました。それは「成功する確率はある一定の値であるが、今は分からない。毎回の試行が独立とする。$n$ 回の試行のうち、$s$ 回成功したとすると、その次の $n+1$ 回目も成功する確率 $p$ は、

$$p=\frac{s+1}{n+2}\tag{1}$$

である。」というものです。はじめて挑戦するプロジェクトが成功する確率は半々のように思われても、一回成功したら、次の成功確率はこの規則で計算すると、

$$p=\frac{1+1}{1+2}=\frac{2}{3}≒0.67\tag{2}$$

と予想できるということです。さすがに最初に成功したのだから、「次も100%成功だ！」は行き過ぎとしても、「試行は独立なのだから、次の成功確率も五割のはずだ！」と言い切るのもどうかと思えます。そもそも隠れた成功確率が今はわからないわけですし、成功した事実は無視できないからです。ここで、ラプラスは、「次に成功する確率は67% だ！」というわけです。

では、二回目も成功だったとします。そうすると、式 $(1)$ より、三回目に成功する確率は、

$$p=\frac{2+1}{2+2}=\frac{3}{4}≒0.75\tag{3}$$

ということになります。この計算を続けると、

表１

	次回も成功する確率
初回成功	67%
二回連続成功	75%
三回連続成功	80%
四回連続成功	83%
・	・
・	・
百回連続成功	99%

 

となります。

ここで、式 $(1)$ に戻って、なぜ試行回数の分母に $2$ を足して、成功回数の分子には $1$ を足すのかという点について考えます。 表1より、100回連続成功しても成功確率はまだ 99%（ 101÷102）です。ちなみに、1000回連続成功しても 99.9%（1001÷1002）で、100% にはなりません。では、こう考えてはどうでしょうか。「プロジェクトを開始する前に、実はすでに成功と失敗が一回ずつあった」と。そうすると、これまで初挑戦といっていたものが実は三回目であって、「初回に成功」といっていたのが「二回目の成功」だった、ということになります。つまり、その時点での成功確率は三分の二で 67%。これで 式 $(2)$ と一致します。一回失敗していたのなら、そのあと何回成功が続いても全体の成功確率が決して 100% にならないのも当然ですね。

ところで、ここまではずっと成功を続けた場合だけをみてきましたが、失敗が一回でも入ったらどうなるでしょうか。図1は一度も失敗しなかったとき（青色の線）と五回目に一度だけ失敗したとき（黄色の線）を比較したものです。一度でも失敗すると次の成功確率がガクッと落ちることがわかります。また、その失敗がずっと後を引くこともわかります。

図1

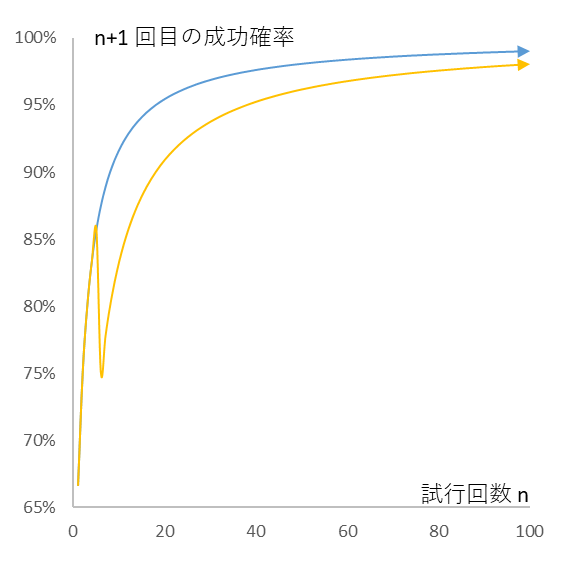
青色の線は一回も失敗しなかったとき、黄色の線は一度だけ（五回目に）失敗したときの成功確率の推移

 

失敗のインパクトはひとつのプロジェクトにかかる時間、労力、コストに比例して大きくなります。典型的な例がロケットの打ち上げです。宇宙開発事業団（現JAXA）の原宣一氏の「少数の属性試験結果から得られるる確信の度合い」という論文（2001）には、「式 $(1)$ から、最初は信頼度 0.5 であったものが、失敗なしに8回連続の成功をみた後で 0.9 まであがり、さらに続けて、失敗なしに 18 回の成功を見てやっと 0.95 まであがる。途中で一回でも失敗するとそのまま試験を続けたのではなかなか信頼度が回復しないこともわかる。失敗原因の究明とその対策が必要なことを示すものである。」とあります。

ただ、人生で我々が挑戦できるプロジェクトは数多くありますし、失敗したからといって国家予算が圧迫されることもありません。失敗の原因究明と対策は大切ですが、四回連続成功したあとに一回失敗したとしても、次の成功確率はまだ 75% もある！と考えてはどうでしょう（図1）。失敗の重みを忘れることなく、チャレンジを続けることが大切ですね。

以上

 

＜参考文献＞

榛葉豊、思考実験、講談社 ブルーバックス、2022、211-212

 

記事一覧へ戻る