2022年6月12日付のブログでは「よつ葉のクローバー」を一本の数式で描く方法を探りましたが、本日は「ハートマーク」に挑戦します。

まずは例によって単位円からスタートします。

$$x^2+y^2=1\tag{1}$$

図１

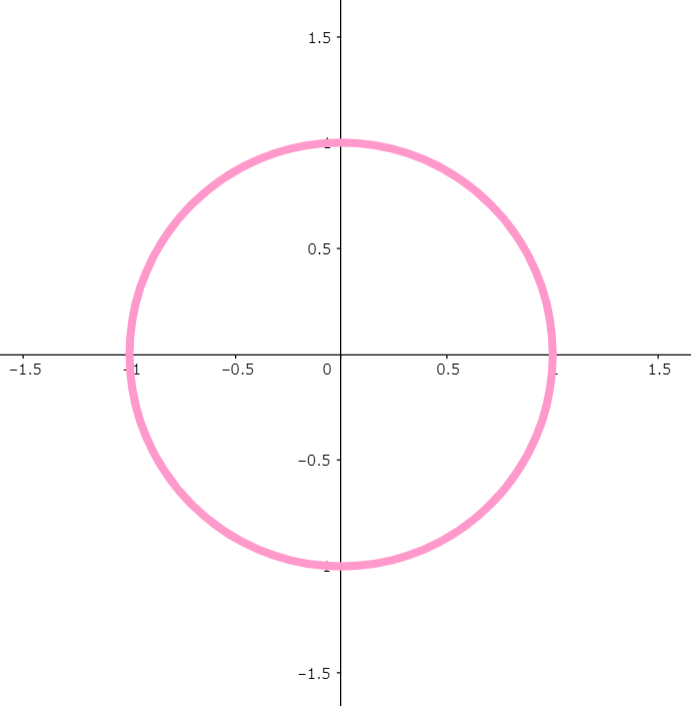
左辺に少し手を加え、二項目の括弧内の $x$ の符号が正の式と負の式のふたつを描きます。

$$x^2+(y-x)^2=1\tag{2a}$$

$$x^2+(y+x)^2=1\tag{2b}$$

図２

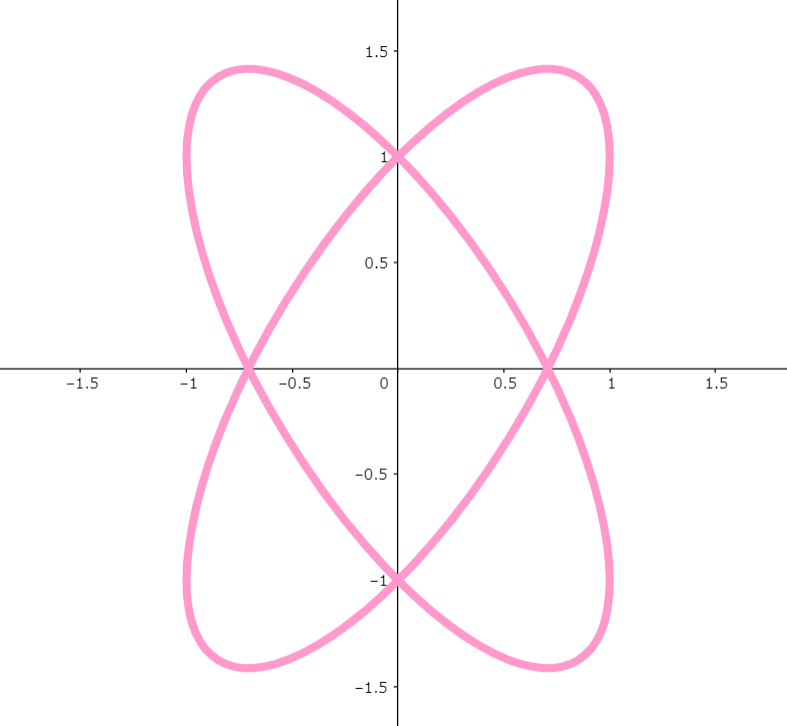
よく見ると、上下左右に四つの「ハートマーク」が描けているのがわかります。

次に左辺第二項の括弧内の $x$ の絶対値をとると、

$$x^2+(y-|x|)^2=1\tag{3}$$

図３

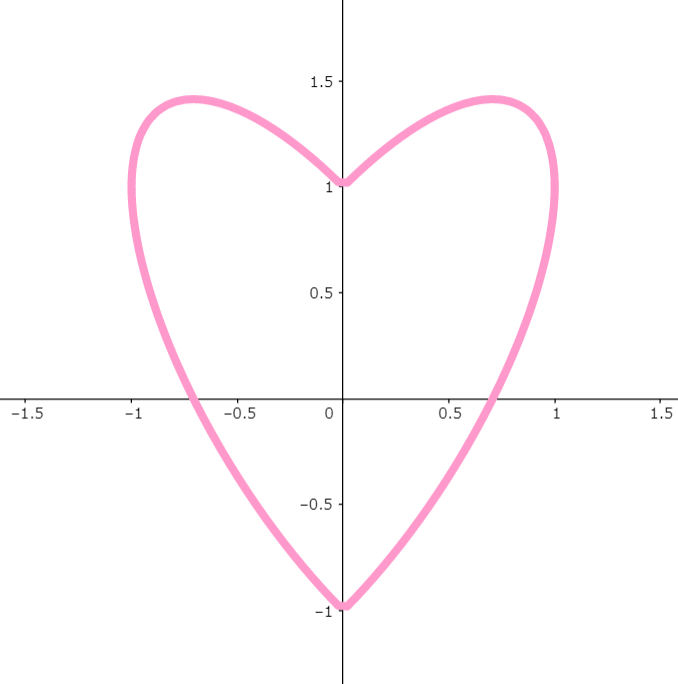
一本の式でいきなり「ハートマーク」ができあがりました。でも、これでは「若葉マーク」のようで、トランプで慣れ親しんだハートと少し違います。

もう少し全体をふっくらさせて、下先に向かう曲線を少し凹ましたいところです。

そこで、左辺第二項の括弧内の $y$ を少し大きくして、$x$ は絶対値の平方根をとります。

$$x^2+(\frac{5}{4}y-\sqrt{|x|})^2=1\tag{4}$$

図５

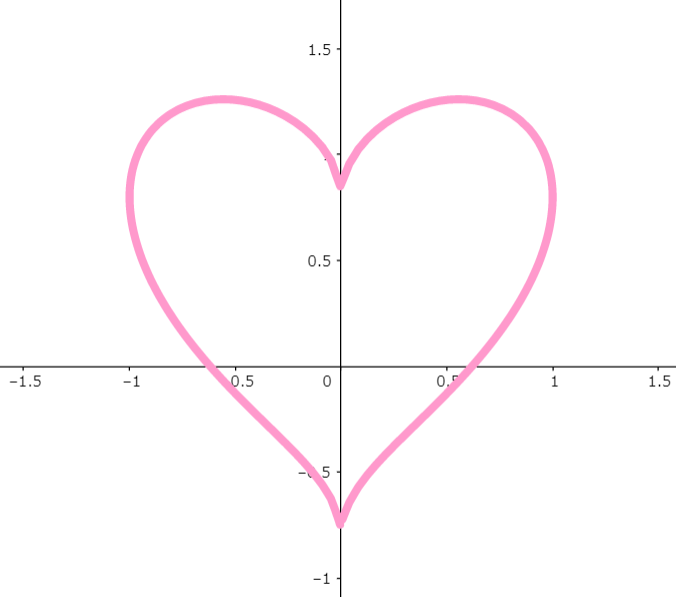
みごとな「ハートマーク」が出来上がりました！

式 $(4)$ は、数学大図鑑（Newton Press) の p65 を参照しました。第二項の $x$ の絶対値のさらに平方根をとってみよう、と思いついたひとは本当にすごいです。

作図はフリーソフトの GeoGebra を使いました。

 

おわり

 

記事一覧へ戻る