Here comes the new year, let’s do our annual forecast of the Nikkei 225 closing price.
The Figure 1 gives an overview of the stock price trends over the 72 years from 1950 to last year 2021. Please note that the vertical axis is logarithmic.
Figure 1

Nikkei 225 Index – 67 Year Historical Chart | MacroTrends
Step 1
Focusing on the daily rate of change of the stock price over the 72 years, classify the number of days that the stock price has risen and fallen, and the respective rate of change into the following four patterns.
Pattern A: Number of days of rise > Number of days of fall, Rate of rise > Rate of fall
Pattern B: Number of days rising > Number of days falling, Rate of rise < Rate of fall
Pattern C: Number of days rising < Number of days falling, Rate of rise > Rate of fall
Pattern D: Number of days rising < Number of days falling, Rate of rise < Rate of fall
Table 1 shows the changes over the past 72 years, categorized by the four patterns.
Table 1 Classification of expression patterns over the past 72 years
| Pattern | Number of occurrences | Average rate of rise | Average rate of fall | Average number of days of rise | Average number of days of fall |
| A | 23 | 0.748% | -0.680% | 134 | 114 |
| B | 24 | 0.815% | -0.886% | 132 | 106 |
| C | 19 | 0.905% | -0.843% | 122 | 127 |
| D | 6 | 1.154% | -1.195% | 118 | 129 |
| 72 |
Step 2
Next, calculate the stock price to be reached at the end of 2022 for each pattern using the formula for stock price prediction.
Formula for predicting the stock price $x_{0}$ in $n$ days
$$x_{n}=x_{0} (1 + a)^p(1 – b)^q$$
$$(p + q = n, a, b > 0)$$.
$x_{0}$ is the initial value; if we are forecasting the closing price in 2022, we set the initial value to 28,791.71 yen, the value of the closing price in 2021. Let $a$ be the average rate of increase, $b$ the average rate of decrease, $p$ the number of days of increase, and $q$ the number of days of decrease.
For the derivation of the formula for stock price prediction, see “How accurate is the prediction of stock price one year from now? “ for more details.
Table 2 shows the result of the calculation using the data in Table 1. For example, there is a 40.9% probability that Pattern A will continue next year, in which case the closing price will be 35,910.72 yen (an increase of 24.7% over the previous year).
Table 2 Closing prices for 2022 predicted using the prediction formula
| Transition Pattern | Number of Occurrences | Probability of Occurrence | Forecast of closing price in 2022 | Percentage change |
| A → A | 9 | 40.9% | 35,910.72 | 24.7% |
| A → B | 6 | 27.3% | 32,718.70 | 13.6% |
| A → C | 6 | 27.3% | 29,268.90 | 1.7% |
| A → D | 1 | 4.5% | 23,738.44 | -17.6% |
| 22 | 100.0% |
Step 3
Finally, we check the above predictions against the probability distribution obtained by the other calculation method. While the stock price tries to increase exponentially, it always fluctuates up and down. The formula for this is
$$\frac{dx}{dt}=rx+vx\frac{dB(t)}{dt}$$
where where $x$ is the stock price, $r$ is the growth coefficient, $v$ is the fluctuation coefficient, and $B(t)$ is the daily random change. This equation represents the moment-to-moment changes in the stock price $x$. The accumulation of these changes is the trajectory of the stock price. The above equation is called a stochastic differential equation, and the calculation of the accumulation is called solving (integrating) the differential equation. The result is
$$x=x_{0}\ e^{(r-\frac{v^2}{2})t+vB(t)}$$
The equation tells us how much the stock price will be when time elapses by t. $x_{0}$ is the initial value. For more information on how to determine $r$ (growth coefficient), $v$ (fluctuation coefficient), and $B(t)$ (daily change), please see my April 21, 2020 blog, “When will the stock market recover from the Corona shock?” for more details. All calculations can be done in Excel.
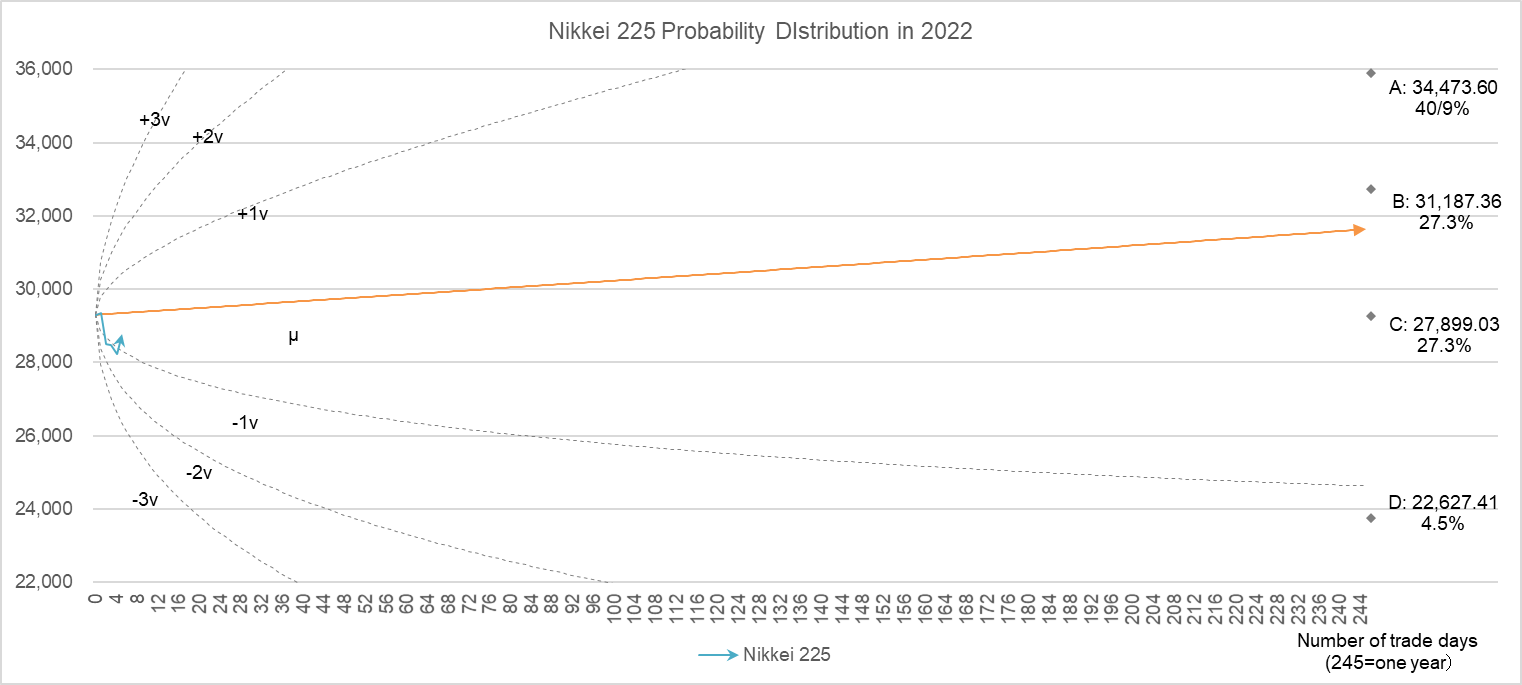
Figure 4 shows the probabilistic distribution of the stock price when the initial value is the closing price in 2020. The orange line $µ$ is the center of the probability distribution, and the dashed lines show $1v, -1v, +2v, -2v…$. The larger the number, the lower the probability of falling into that range. Then, superimpose the four predictions above. We can see that they are all within the range of $pm 1v$ and there is no contradiction.
Figure 2 Probability distribution of Nikkei 225 and prediction of closing price at the end of 2022
The above is the forecast calculation. We will continue to check the forecast against the actual Nikkei 225 once a week this year!
The End
Back to archive