数理経営のすすめその４「クラスター効果」- 単独では成し得ない成長の数理的意味

2021年6月10日付のブログ、数理経営のすすめその３で「競争と共創」が二社の未来を、どのように変えるのかを数理的に解析し、比較しました。本日は、その解析の対象を二社からクラスターへ発展させます。クラスターは通常、同業種の地理的な集まりをいうことが多いかと思いますが、ここでは異業種もふくめた事業体の集まりをクラスターととらえて議論します。

二社の場合、各社の成長の変化率は以下の数式で示されました。

$$\frac{dx}{dt}=r_{1}x(1+\frac{x}{K_{1}})+axy\tag{1}$$

$$\frac{dy}{dt}=r_{2}x(1+\frac{y}{K_{2}})+bxy\tag{2}$$

r は成長係数、K は経営者目線、a と b が競争係数です。a は x に対する y の影響、b は y に対する x の影響で、敵対する場合はマイナス、協力しあう場合はプラスです。おなじ要領で三社（x,y,z）に増やすと、

$$\frac{dx}{dt}=r_{1}x(1+\frac{x}{K_{1}})+axy+bxz\tag{3}$$

$$\frac{dy}{dt}=r_{2}x(1+\frac{y}{K_{2}})+cyx+dyz\tag{4}$$

$$\frac{dz}{dt}=r_{3}x(1+\frac{z}{K_{3}})+ezx+fzy\tag{5}$$

となります。さらに五社（x,y,z,v,w）に増やすと、

$$\frac{dx}{dt}=r_{1}x(1+\frac{x}{K_{1}})+axy+bxz+cxv+dxw\tag{6}$$

$$\frac{dy}{dt}=r_{2}x(1+\frac{y}{K_{2}})+eyx+fyz+gyv+hyw\tag{7}$$

$$\frac{dz}{dt}=r_{3}x(1+\frac{z}{K_{3}})+izx+jzy+kzv+lzw\tag{8}$$

$$\frac{dv}{dt}=r_{4}x(1+\frac{v}{K_{4}})+mvx+nvy+ovz+pvw\tag{9}$$

$$\frac{dw}{dt}=r_{5}x(1+\frac{w}{K_{5}})+qwx+rwy+swv+twv\tag{10}$$

となります。一見、複雑にみえますが、影響を与えたり受けたりする相手がふえるので、式が長くなっているだけです。

その３ で、二社がお互い助け合うと、その成長の度合いは一社だけのものよりも大きくなることをみました。そうすると、二社が三社、さらに五社と増えるとさらに成長の度合いが大きくなることが予想されます。では実際に計算してみましょう。

計算に使用する係数は表１と表２のとおりとします。

表１　成長係数と経営者目線

		成長係数		経営者目線
x	r₁	0.2	K₁	50
y	r₂	0.3	K₂	70
z	r₃	0.4	K₃	90
v	r₄	0.5	K₄	100
w	r₅	0.2	K₅	80

表２　共創係数

–	–	e	0.0002	i	0.0001	m	0.0003	q	0.0002
a	0.0002	–	–	j	0.0003	n	0.0002	r	0.0001
b	0.0001	f	0.0003	–	–	o	0.0002	s	0.0001
c	0.0003	g	0.0002	k	0.0002	–	–	t	0.0003
d	0.0002	h	0.0001	l	0.0001	p	0.0003	–
平均	0.0002		0.0002		0.0002		0.0003		0.0002

これらの係数を式 (6) から (10) に代入して、プレイヤーの数が二社→三社→五社と増えたときの平衡値を計算した結果が表３です。

表３各社が到達する平衡値と単独上限数値からの増加率

x		y		z		v		w
平衡値	増加率	平衡値	増加率	平衡値	増加率	平衡値	増加率	平衡値	増加率
50	–	–	–	–	–	–	–	–	–
54	7%	71	2%	–	–	–	–	–	–
61	22%	80	14%	97	8%	–	–	–	–
71	43%	89	28%	105	17%	119	19%	108	35%

注）各社の初期値はいずれも 1.0 として計算した平衡値と単独上限値からの増加率

確かにクラスターを構成するメンバーの数が増えれば増えるほど成長の度合いが大きくなっているのがわかります。五社クラスターとしての平衡値は 492 (=71+89+105+119+108) で、各社単独の上限（経営者目線）の合計である 390 (=50+70+90+100+80) を 26% 上回っています。

各社の成長軌跡と成長速度の推移は以下のとおりです。

図１

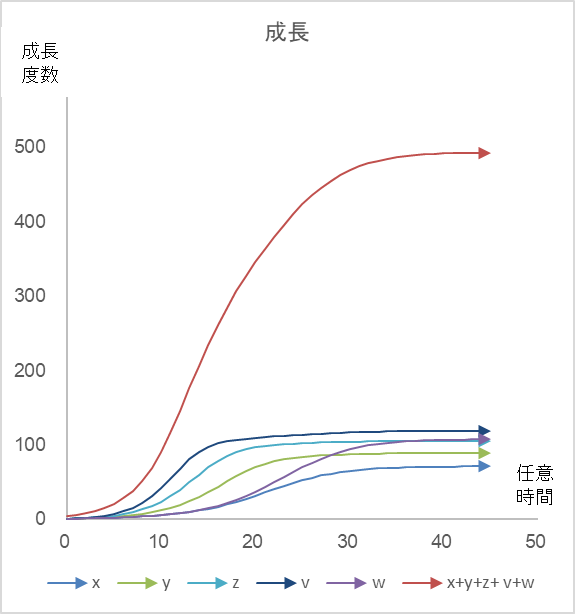
各社の成長の軌跡。t=0での初期値は各社いずれも 1.0とし、計算には表1と表2の係数を使用した。

図２

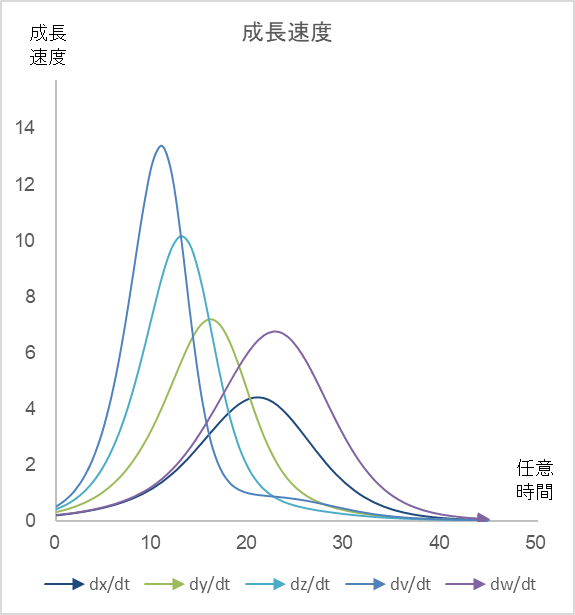
図１の成長をもたらす各社の成長速度の軌跡

ここではわかりやすいように、クラスターの構成メンバーを五社に絞りましたが、式 (6) ～(10) は、10社、100社、といくらでも拡張することができます。構成メンバーが増えれば各社の共創係数をどんどん小さくしていったとしても、その効果は無視できません。

商店街には同業者がたくさんいるから、離れた場所に出店した方がいいという考えもわかりますが、これは商店街への出店を、マイナスの「競争係数」だけでとらえていることを意味します。商店街は同業者だけではなく異業種の店もたくさん軒を連ねています。多種多様な店が集まっているところにひとが集まります。各社が能動的にたすけあいをしているわけではありませんが、クラスターを構成することで、結果として受動的なたすけあいをしていることになるわけです。

図1の赤い実線をご覧ください。これがクラスターの成長です。成長するクラスターはいつも賑わっています。同業者との競争を心配するよりも、同業者と異業者が共存共栄するクラスターに属しているほうが賢明な選択だといえそうです。

念のため計算で確かめてみましょう。まずは、前提条件を定めます。

＜前提条件＞

①　x と y は同業者でライバル。お互いの影響を受けやすい。y が後発。

②　z は x、y の同業者だがポジショニング戦略で、両者の影響を受けない。

③　 v と w は異業種だがゆるやかなコラボ関係にある。

④　x、y、z、v、w は地理的なクラスターを構成している。

図3

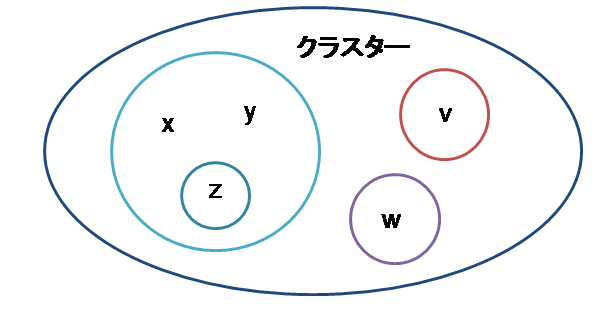
表４　初期値、成長係数、経営者目線

		初期値		成長係数		経営者目線
x	x₀	50	r₁	0.2	K₁	50
y	y₀	20	r₂	0.3	K₂	70
z	z₀	1	r₃	0.4	K₃	90
v	v₀	50	r₄	0.5	K₄	100
w	w₀	40	r₅	0.2	K₅	80

注）先発組は初期値を高く設定しています。

表５　競争と共創係数

		e	-0.0003	i	0.0001	m	0.0003	q	0.0002
a	-0.0003	–	–	j	0.0001	n	0.0002	r	0.0001
b	0.0001	f	0.0001	–	–	o	0.0002	s	0.0001
c	0.0003	g	0.0002	k	0.0002	–	–	t	0.0003
d	0.0002	h	0.0001	l	0.0001	p	0.0003	–	–
平均	0.00008	平均	0.00003	平均	0.00013	平均	0.00025	平均	0.00018

前提条件にもとづき、x と y は競争関係にあるためマイナスの係数にしています。

図４

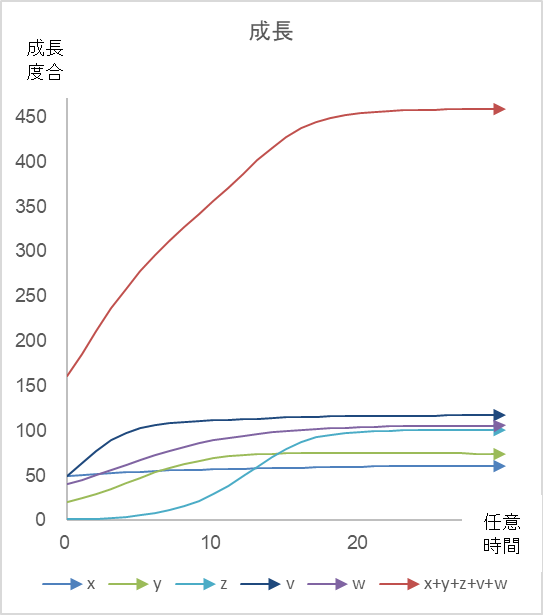
表４、表５の各係数を、式 (6)～(10）に代入して得られる各社の成長軌跡。

図５

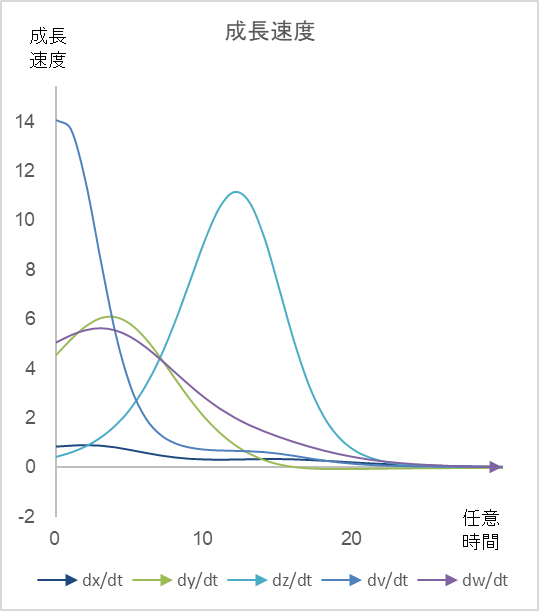
図４の成長をもたらす各社の成長速度

ここで、ライバル同士である x と y に注目します。もし、x と y が二社でだけでしのぎを削ったとすると、その３ でみたように、両者ともに成長が抑制されて、その平衡値は x が 45、y が 67 となり、単独の上限値である 50 と 70 を下回ります。しかしながら、クラスターに属したことによって、x と y のマイナスの競争係数が、他のクラスター構成員の共創係数によって打ち消され（表５）、平衡値は x が 61 へ、y が 75 に増えています（表６）。

表６

		単独		五社クラスター		二社間の競争
		上限値		平衡値		平衡値
x	K1	50	→	61	←	45
y	K2	70	→	75	←	67

x と y はクラスターに属することで、単独上限値を超える成長を達成することができる。

計算の詳細にご興味があるかたは、クラスター効果 – Excel をご覧ください。

つづく

記事一覧へ戻る

ブログ

数理経営のすすめ その４「クラスター効果」- 単独では成し得ない成長の数理的意味