数理経営のすすめ その５「地理的成長①」では、たったひとつの方程式によって、時間的かつ空間的な成長（以下、まとめて「時空間成長」と呼びます）を表現できることをお伝えしました。その数式は、

$$\frac{∂n}{∂t}=D\frac{∂^2n}{∂x^2}+rn(1-\frac{n}{K})\tag{4}$$

        ↑　        ↑      ↑

                                                                 　　拡散項　 　 成長項      上限項（n=Kとなった時点で成長が止まる）

 

でした。驚くべきことにこの一本の数式から、下のような時空間成長を導くことができます。横軸 x が空間、縦軸 n が成長の度合いです。

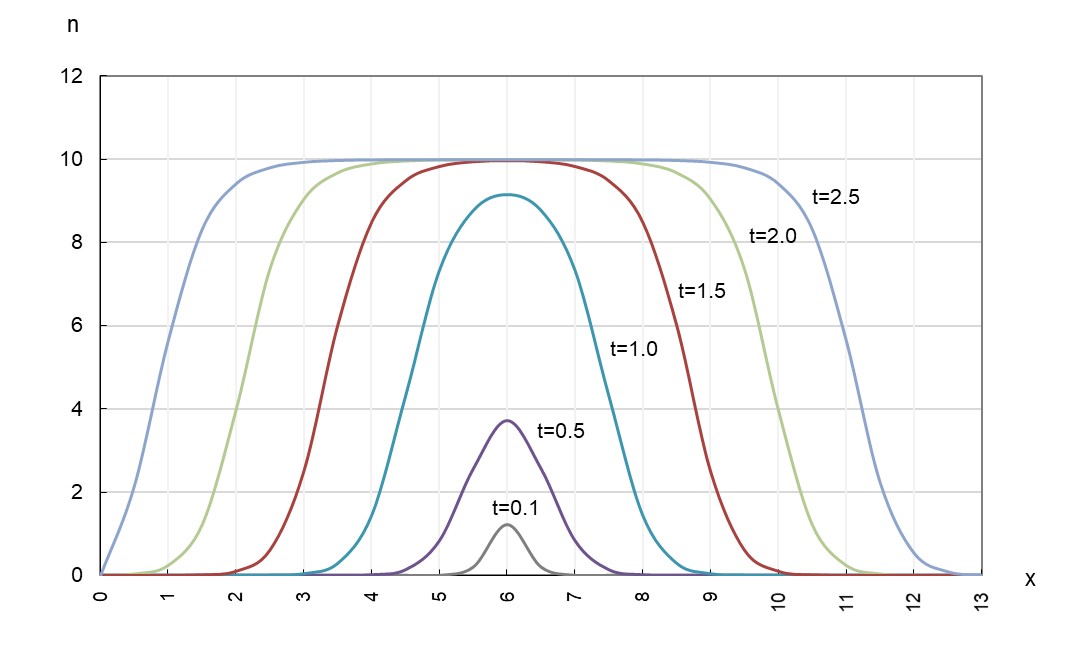
D=0.5、r=0.7、K=10（⊿x=0.5、⊿t=0.1）

場所 x₆ から、初期値 1.0 で時空間成長する様子（地理的境界 x_0、x₁₃）

 

さて、今回はプレイヤーを五社（n₁, n₂, n₃, n₄, n₅）としますので、数式は五つ必要です。必要な要素が拡散項、成長項、上限項の三つであることは、一社のときと同じです。ただ、上限項の中に五社が相互に影響し合う構図を組み込みますので少し長くなります。

$$\frac{∂n_{1}}{∂t}=D\frac{∂^2n_{1}}{∂x^2}+r_{1}n_{1}(1-\frac{n_{1}+b_{1}n_{2}+c_{1}n_{3}+d_{1}n_{4}+e_{1}n_{5}}{K_{1}})\tag{1}$$

$$\frac{∂n_{2}}{∂t}=D\frac{∂^2n_{2}}{∂x^2}+r_{2}n_{2}(1-\frac{a_{2}n_{1}+n_{2}+c_{2}n_{3}+d_{2}n_{4}+e_{2}n_{5}}{K_{2}})\tag{2}$$

$$\frac{∂n_{3}}{∂t}=D\frac{∂^2n_{3}}{∂x^2}+r_{3}n_{3}(1-\frac{a_{3}n_{1}+b_{3}n_{2}+n_{3}+d_{3}n_{4}+e_{3}n_{5}}{K_{3}})\tag{3}$$

$$\frac{∂n_{4}}{∂t}=D\frac{∂^2n_{4}}{∂x^2}+r_{4}n_{4}(1-\frac{a_{4}n_{1}+b_{4}n_{2}+c_{4}n_{3}+n_{4}+e_{4}n_{5}}{K_{4}})\tag{4}$$

$$\frac{∂n_{5}}{∂t}=D\frac{∂^2n_{5}}{∂x^2}+r_{5}n_{5}(1-\frac{a_{5}n_{1}+b_{5}n_{2}+c_{5}n_{3}+d_{5}n_{4}+n_{5}}{K_{5}})\tag{5}$$

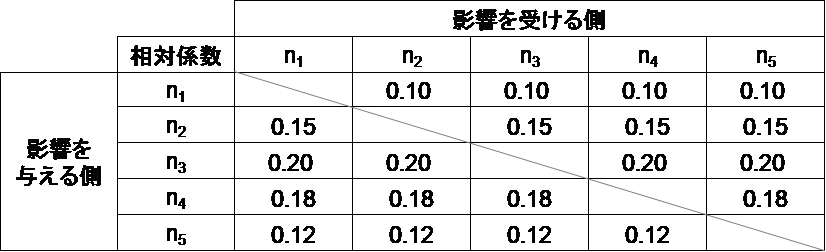
D は拡散係数、r  は成長係数、K は成長上限、a,b,c,d,e は相対係数です。a は n₁ が 他社 へ与える影響、b は n₂ が他社へ与える影響、c はn₃ が他社へ与える影響、d は n₄ が他社へ与える影響、e は n₅ が他社へ与える影響です。相対係数が正の値の場合は他社の売上を減少させる力（競争関係）となります。値が大きくなると競争相手を淘汰してしまうこともあります。一方、負の場合は相手の売上を増加させる力（共創関係）となります。オープンイノベーションやクラスター効果 などがその事例です。

また、各社はそれぞれ近接する場所で、同時に同じ初期値（=1.0）で事業をはじめたとします。

では早速、式 (1) ～ (5) に具体的な係数を設定して成長の時空変化をみてみましょう。

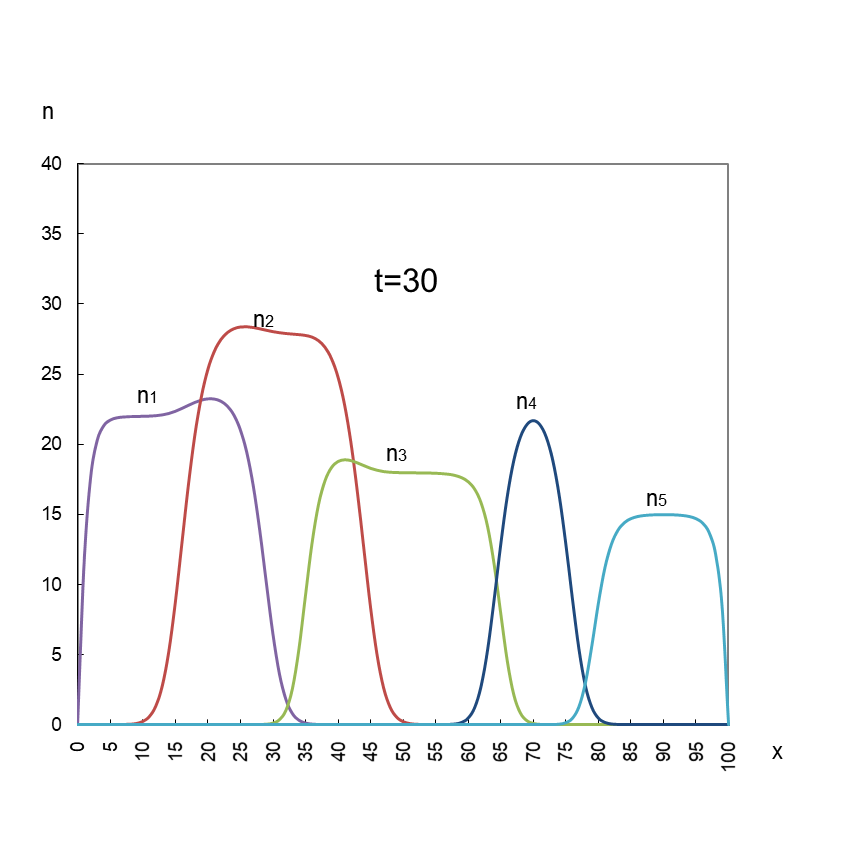
まずは競争しながらも共存するパターンです。

図１

　

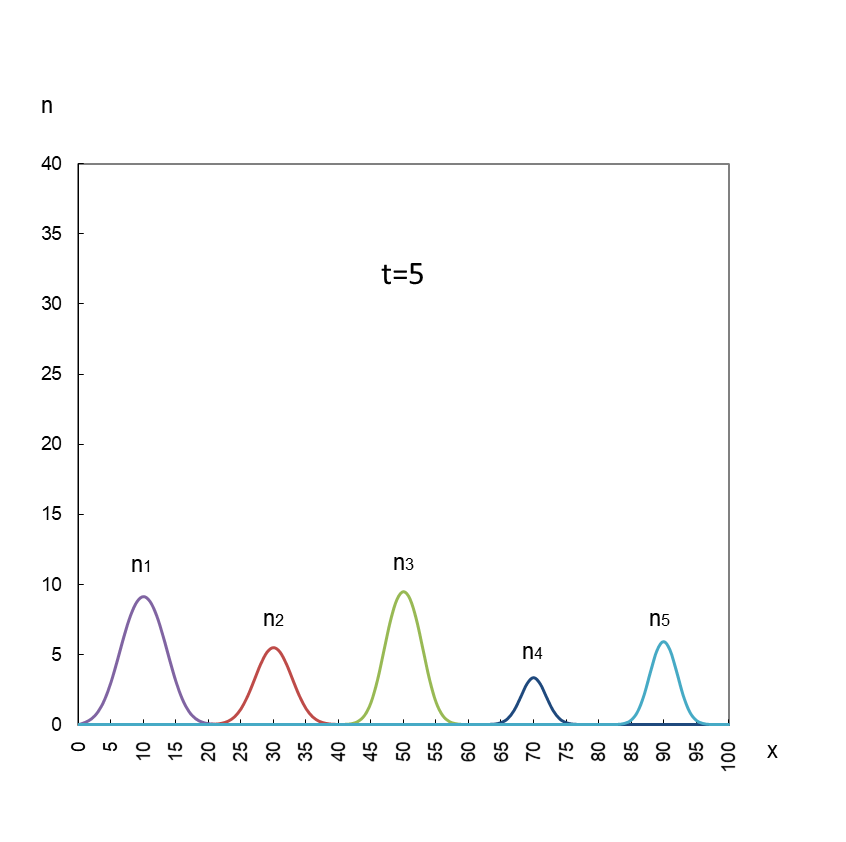
五社は共存するが、お互いに足を引っ張り合っているため成長の平衡値が単独で達成し得る上限値（K_1～5）を下回っている。

 

計算に用いた係数は以下のとおりです。

 

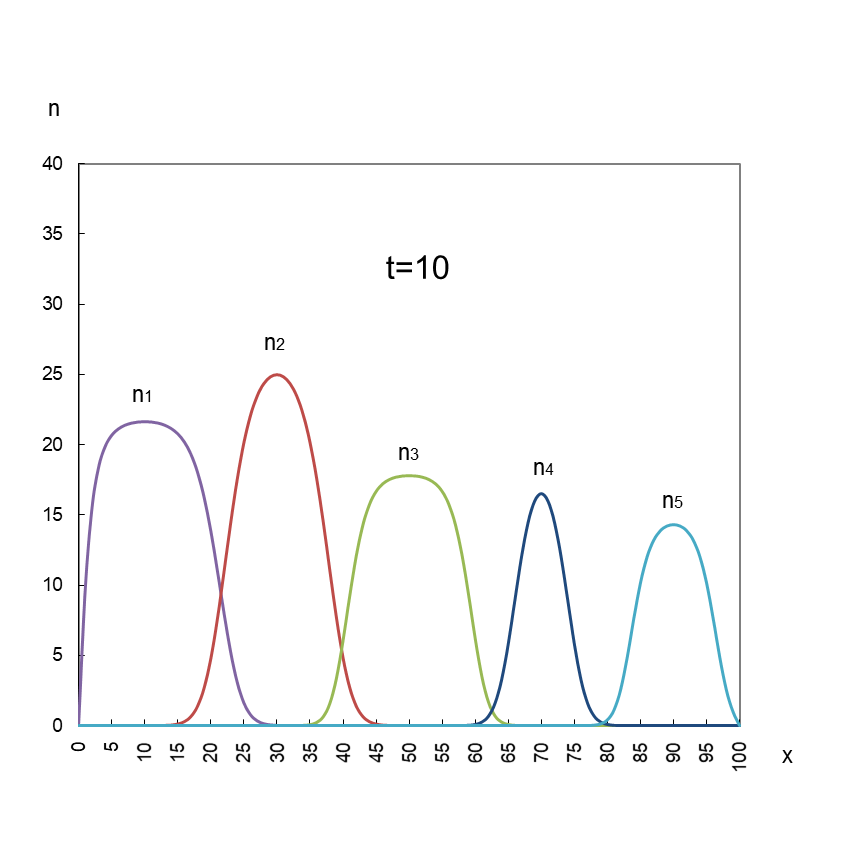
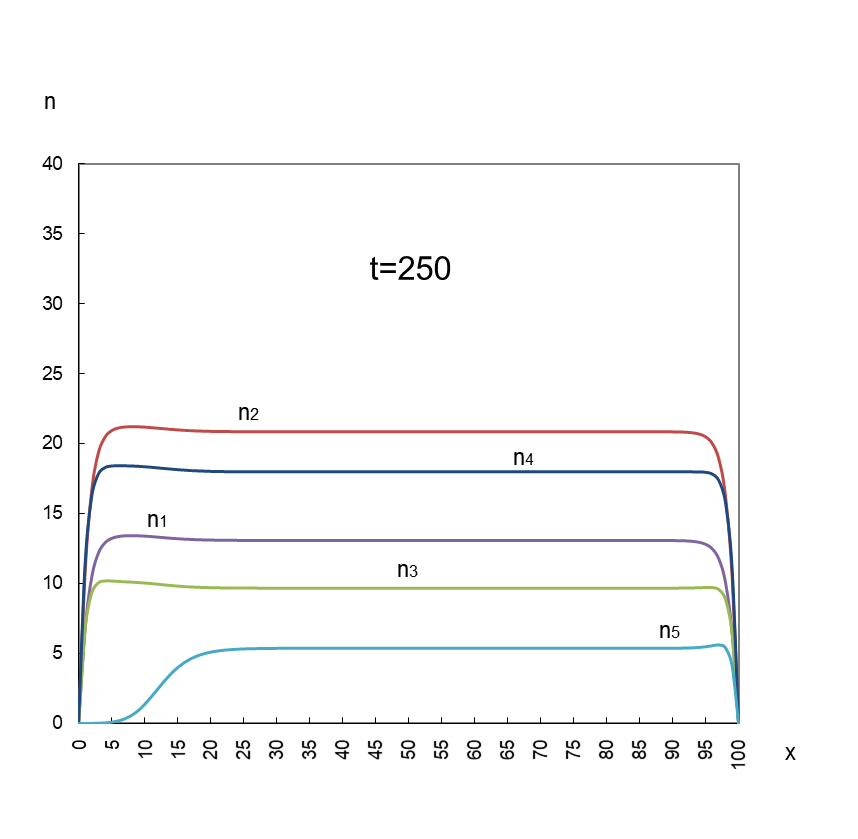
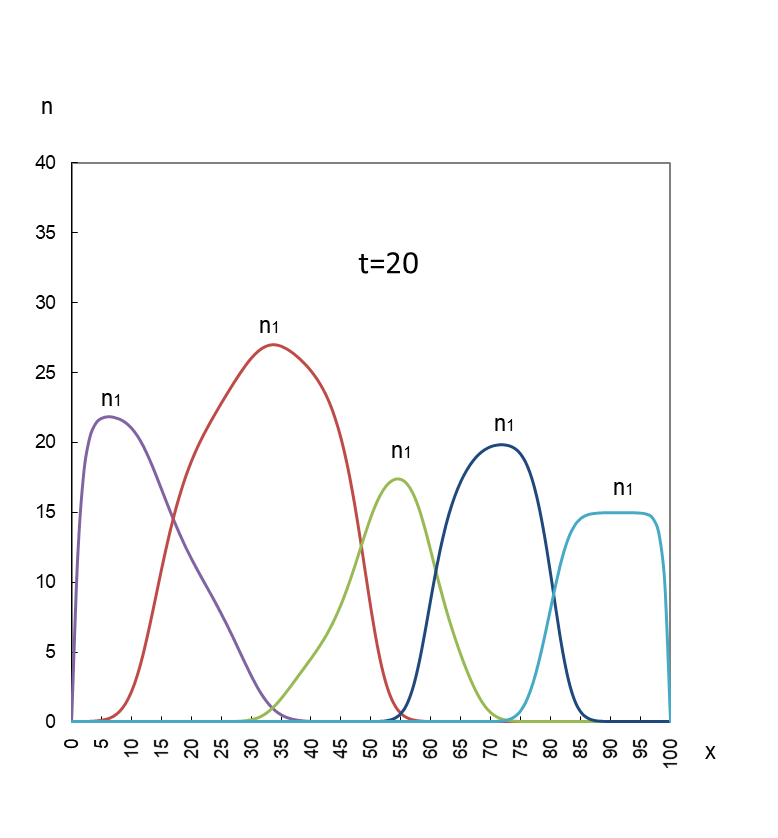
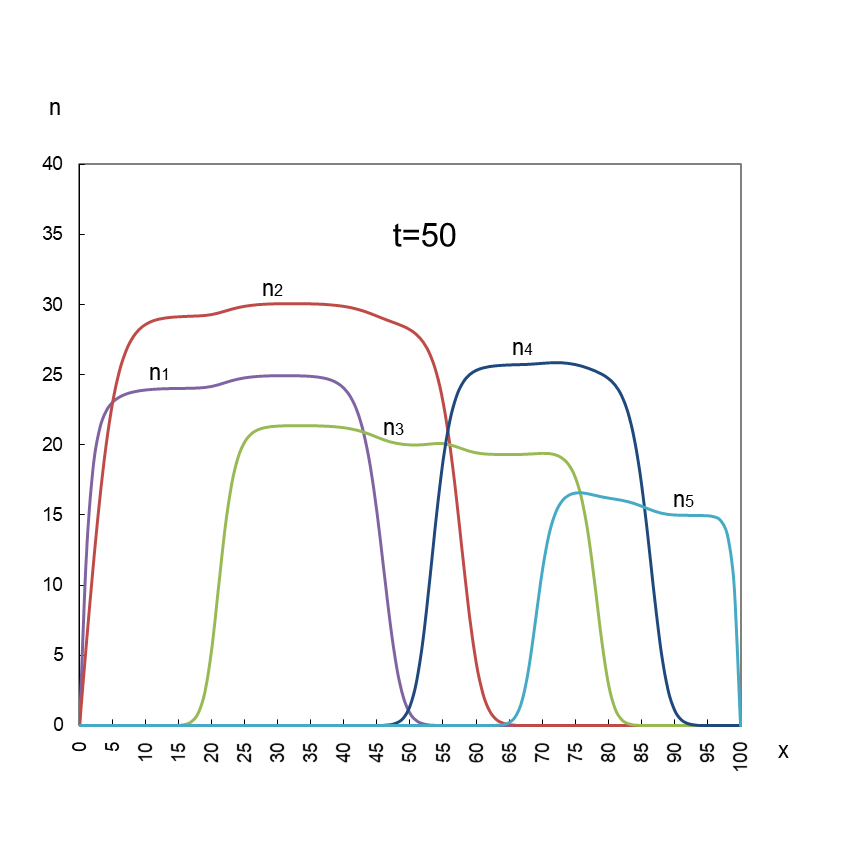
次は、競争に勝敗がつくパターンです。お互いが出合い、重なり合う t=20 以降にスポットを当てます。

図２

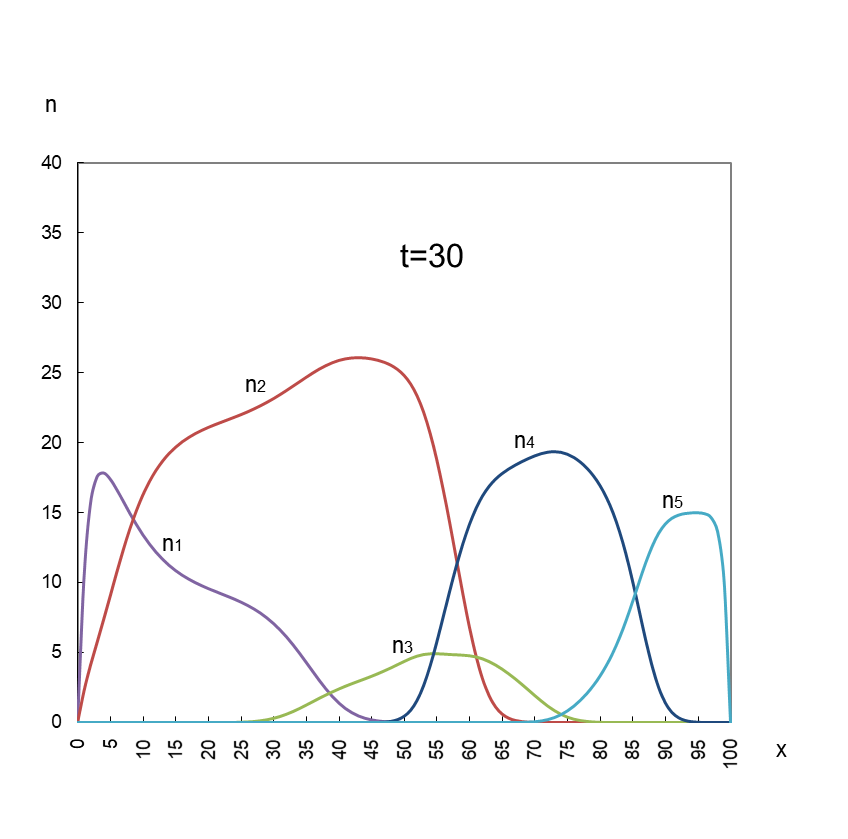
n₃ と n₅ が競争に負けて淘汰されている。

勝ち残った三社の成長平衡値は、お互いに足を引っ張り合っているため、単独で到達し得る上限値（K_1～5）を下回っている。

 

計算に用いた相対係数は以下のとおり（その他の係数は図１と同じ）です。

 

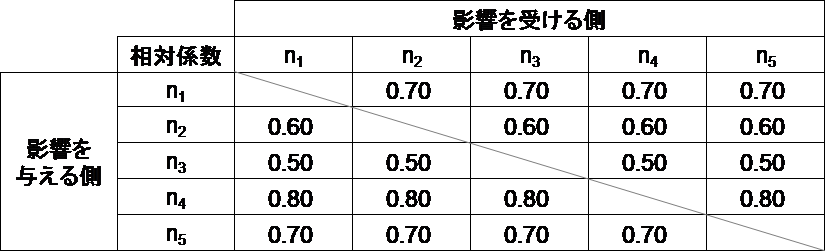
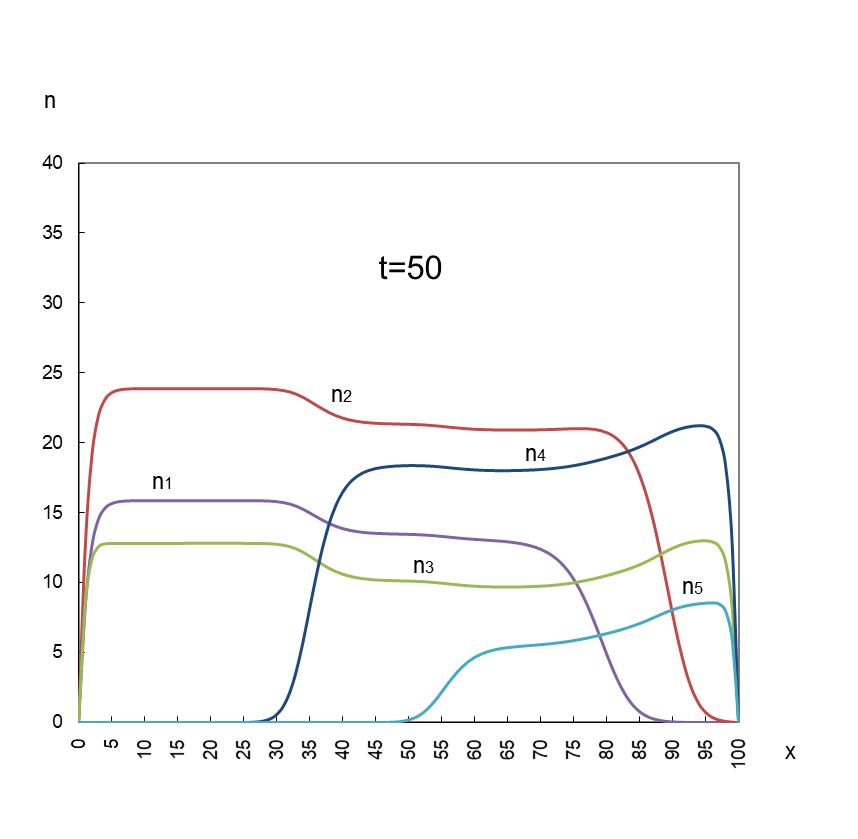
最後は五社がお互いに助け合うバターンです。

図３

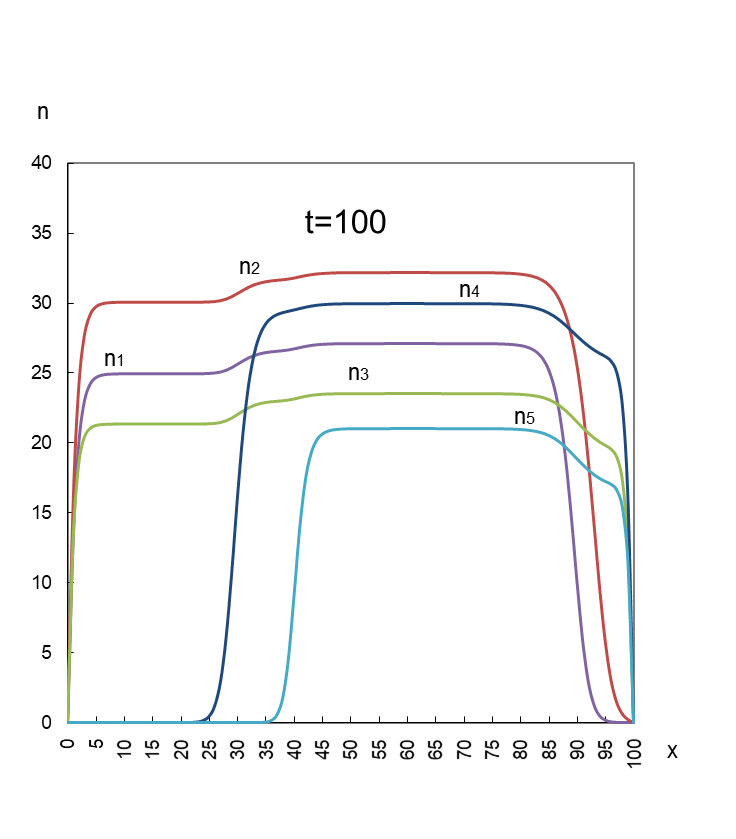
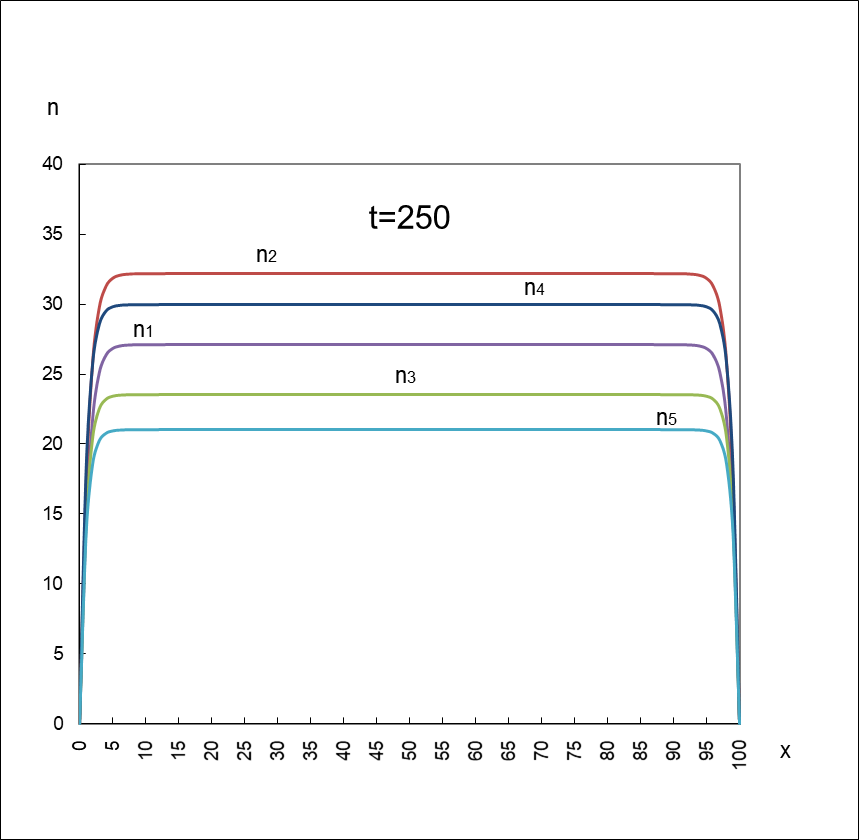
五社が共創共栄することで各社の平衡値は単独の上限値（K_1～5）を上回っている。

 

計算に使用した相対係数は以下のとおり（その他の係数は図１と同じ）です。符号が負であることにご注目ください。

 

では、ここで五社の成長を合算して比較します。図４をご覧ください。

図４

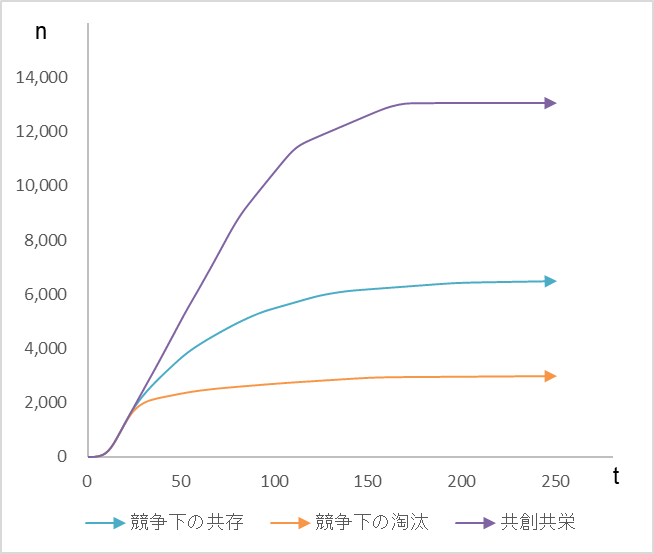
三つのパターンの五社合算比較

 

三つのパターンの内、最も成長度が低いのは激しい競争を繰り広げ、二社が淘汰されてしまったパターンです。一方、最も成長度が高いのはお互いが成長にプラスの影響を与え合う共創パターンです。積極的な協力でなくても地理的なクラスターを構成するだけで各社が低い相対係数をもちよることになり、単独では不可能な成長を遂げることができます。

これはつまり、業界や市場の成長は、ライバルを打ち負かすことではなく、各社が特長を活かしつつ創意工夫をするとともに、地理的にも近接することによって、成し遂げられるということを意味しておりたいへん興味深いといえます。また、同業者に加えて、異業種が集まることによってもその地域の集客力が向上し、関連支援業者の数や種類も多くなる（利便性が高まりコストも下がる）こと、などもクラスター効果といえます。

今回の計算に使った係数は仮の値ですが、事実にもとづくデータを地道に積み重ねることによってより現実的な係数を導出することができます。そしてより正確に自社や業界の未来を予測できるようになるでしょう。

以上

PS.　今回はエクセルのデータ量が WORDPRESS の許容範囲を超えるためリンクを貼ることができませんでした。申し訳ありませんが、計算の詳細にご興味のある方は「問い合わせ」ページからご要望ください。

記事一覧へ戻る