「数理経営のすすめ その１～４」でいろいろな成長パターンや他社との競争や共創が成長にどのような影響を与えるかを数理的に解析しましたが、本日は少し視点を変えて、地理的な成長にスポットをあてます。成長させたいものが売上であれば、その売上の時間的かつ空間的なひろがりをみようということです。

ある物質がランダムに動きながら拡散する様子は次の偏微分方程式で表せることがわかっています。

$$\frac{∂n}{∂t}=D\frac{∂^2n}{∂x^2}\tag{1}$$

ここで、n は個体数、t は時間、x は場所、D は拡散係数です。方程式だけをみてもこれがどういう現象なのかがわかりませんので、早速、グラフにしてみましょう。図1をご覧ください。縦軸が個体数  n、横軸が場所 x です。最初、場所 x = 0（以下 x₀）に100 の個体が集まっているところからスタートします。時間経過とともに100 個がランダムに拡散（ブラウン運動）するとします。釣鐘型の曲線はそれらの個体が存在するであろう確率的な位置（確率密度）を示しています。

図１

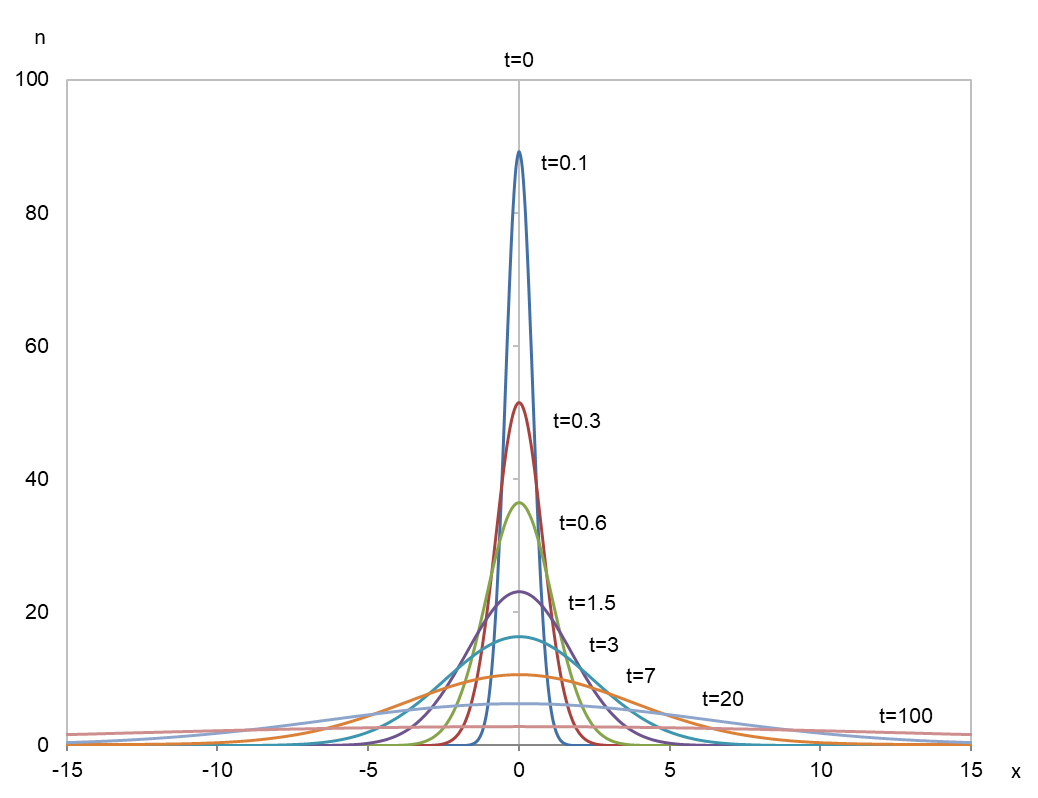
式 (1) で、D=1.0 としたときの解曲線

個体（総数100）が x = 0 で放たれ、ランダムな運動によって広がる様子

 

 

式 (1) を解いて、位置 x と時間 t の関数で表すと、

$$f(x,t)=\frac{N}{\sqrt{4πDt}}e^{-\frac{x^2}{4Dt}}\tag{2}$$

となります。N は個体の総数です。ちなみに平均 µ 、分散が σ² の確率密度関数（正規分布）は、

$$f(x)=\frac{1}{\sqrt{2πσ^2}}e^{-\frac{(x-µ)^2}{2σ^2}}\tag{3}$$

ですから、式 (2) は分散 2Dt の正規分布であることがわかります。

さて、唐突ですが、ここでねずみの話です。1905年に檻から逃げ出した五匹のマスクラット（北アメリカ原産、写真）はその後数十年間の間にヨーロッパ中にひろがり数百万匹に増えました。図2は1927年までの分布の範囲を記したものです。

マスクラット

頭から尻尾の先まで約50センチ（Wikipedia）

図２

ヨーロッパにおける1905年～1927年のマスクラットの分布の範囲（数理生物学入門 p101、巌佐、2006）

 

ところで、図1は拡散はしていますが、成長はしていません。個体数に変化がないからです。我々が達成したいのは個体数の増加をともなう地理的な成長です。まさにマスクラットのような成長です。そのためには式 (1) に成長をもたらす項を追加する必要があります。ここでは、市場規模や経営者目線を計算に取り込める成長項を加えてみましょう。（上限のある成長については、数理経営のすすめ その１「成長」を参照してください。）

$$\frac{∂n}{∂t}=D\frac{∂^2n}{∂x^2}+rn(1-\frac{n}{K})\tag{4}$$

        ↑　        ↑      ↑

                                                                 　　拡散項　 　 成長項      上限項（n=Kとなった時点で成長が止まる）

 

r は成長係数、K は上限値です。この式 (4) に具体的な係数を代入して各地点の成長を計算した結果が図3です。

図３

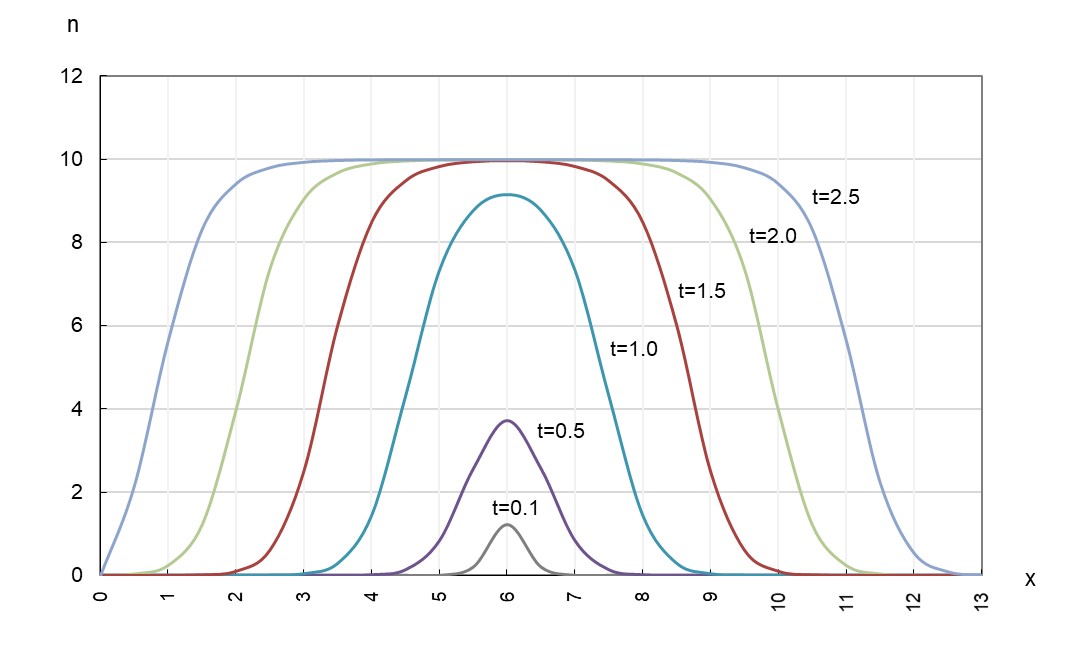
D=0.5、r=0.7、K=10（⊿x=0.5、⊿t=0.1）

場所 x₆ から、初期値 1.0 で拡散ロジスティック成長がはじまるときの時間推移（地理的境界 x_0、x₁₃）

 

各波の先端に注目してください。間隔がほぼ同じです。実際、波の先端（フロント）の移動速度も計算することができて、$2\sqrt{rD}$ です。図３であれば、$2\sqrt{0.7*0.5}≒1.2$ になります。ここで、図２のマスクラットの分布線をもう一度ご覧ください。この線は人間の目にはじめてとまった場所を示していますので、ほぼ、図３のフロントにあたると考えていいでしょう。

さて、図３は 例えると、x₆ に初出店して、 

x₆ → x₅ → x₄ → x₃ → x₂ → x₁

x₆ → x₇ → x₈ → x₉ → x₁₀

と、店舗を増やしている、つまり、地理的拡大をしていることに相当します。では、それぞれの店舗の売上はどう推移しているでしょうか。図４をご覧ください。各店舗はそれぞれ上限 10 のロジスティック成長をしています。

図４

各店舗は時間の差はあれ、上限 K=10 のロジスティック成長をする。

 

図５は各店舗の成長をひとまとめにしたものです。一か所で成長する限り上限は 10 ですが、地理的な拡がりを実現することによって約25 倍の成長を遂げたことになります。

図５

売上の合計（単独店舗の約25倍）

 

式 (4) は外来の病原体が新たな土地に侵入して、増殖しながら次第に広がる様子も表現することができます。図６は14世紀中ごろに黒海と地中海を経由してヨーロッパ全土に伝播した黒死病（ペスト）です。フロントがほぼ一定の速度 （$2\sqrt{rD}$） で進んでいるのがわかります。

図６

14世紀に流行したペストのフロント移動。矢印は海路による伝播。

死者数は当時のヨーロッパの人口の三分の一から三分の二に当たる二千万から三千万人と推定されている（感染症の世界史、石弘之、2018）。

 

つづく

PS. 計算の詳細にご興味のある方は、地理的成長① – Excel をご覧ください。

記事一覧へ戻る