あなたはある組織のリーダーです。組織にはもちろん目指す目標があります。しかし、昨今、リーダーに求められるのは組織目標の達成だけではありません。部下がコンプライアンス違反をするとあなたの評価は一気に下がります。部下には気持ちよく働いてもらいたいが、コンプライアンス違反をやられては困る、かといってあまりうるさく言ってやる気をなくされても困る。これはどのような組織においてもそのリーダーが多かれ少なかれ持っている共通の悩みではないでしょうか。

さて、突然ですが、以上のような状況を数式で表現できるでしょうか。部下がコンプライアンス違反をしないように管理することを圧力 $P$ （Pressure）とします。一方、部下の活力を $V$（Vitality）とします。経験的に、圧力 $P$ が大きいと活力 $V$ は小さくなり、逆に、圧力 $P$ が小さいと活力 $V$ は大きくなりそうです。よって、$P$ と $V$ の積は一定としましょう。

$$PV=一定\tag{1}$$

部下の活力を左右するのは、リーダーからのプレッシャーだけでなく、部下が組織から受ける待遇（昇進、年収など）もありますが、ここではその待遇は一定であると仮定します。式$(1)$を図示すると、

図１

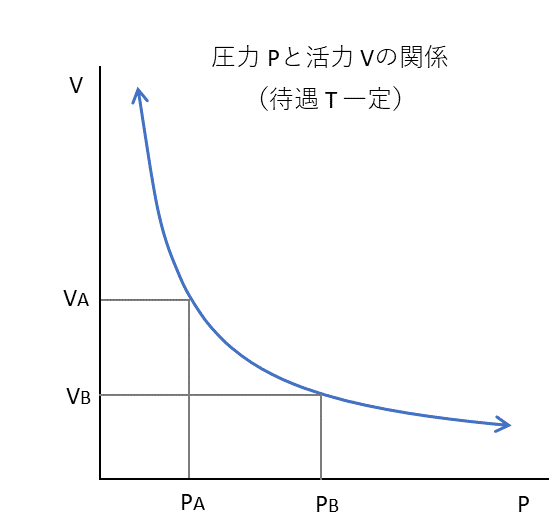
待遇 $T$ が一定なら、圧力 $P$ を大きくすると活力 $V$ は小さくなり、$P_{A}V_{A}=P_{B}V_{B}$  が成り立つ。

 

となります。次に、リーダーの圧力 $P$ が一定のときを考えましょう。待遇をよくすれば部下の活力が高まることは経験的にわかります。自分が部下のときもそうでしたね（笑）。待遇を $T$（Treatment）とします。偶然ですが、日本語も英語も頭文字は $T$ です。待遇 $T$ と活力 $V$ はプラスの比例関係にあるということですから、その比が一定ということです。つまり、

$$\frac{V}{T}=一定\tag{2}$$

式$(2)$を図示すると、

図２

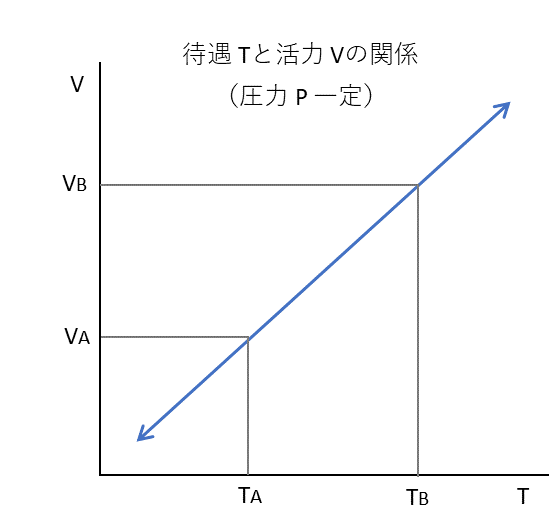
圧力 $P$ が一定なら、待遇 $T$ を大きくすると活力 $V$ も大きくなり、$\frac{V_{A}}{T_{A}}=\frac{V_{B}}{T_{B}}$  が成り立つ。

 

冒頭に述べたとおり、リーダーの関心は、部下の活力を維持しながら、コンプライアンス違反防止を強化することにあります。どうすればいいでしょうか？図１より、圧力 $P$ を高めると活力 $V$ が下がりますから、活力 $V$ を維持したいのであれば、図２より待遇 $T$ をよくしなければなりません。つまり、圧力 $P$ だけを増やしてもだめで、同時に待遇もよくしなければならない、ということです。図３をご覧ください。

図３

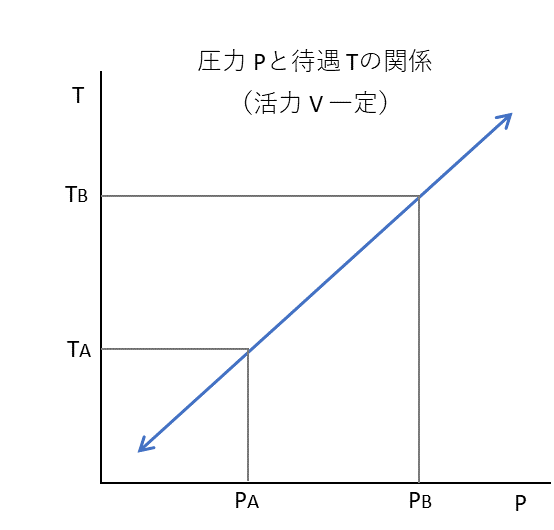
圧力 $P$ を高めたいなら同時に待遇 $T$ もよくしないと活力 $V$ は維持できない。$\frac{P_{A}}{T_{A}}=\frac{P_{B}}{T_{B}}$ が成り立つ。

 

さて、ここまで来ると、高校の物理で熱力学を学んだ方は「あれっ？」とお気づきでは。実は、式$(1)$はボイルの法則、式$(2)$はシャルルの法則とまったく同じ形をしています。ボイルの法則 $PV=一定$ の $P$ は気体の圧力、$V$ は気体の体積（Volume）、シャルルの法則 $\frac{V}{T}$の $V$ も気体の体積、$T$は気体の温度^＊（Temperature）です。式 $(1)$ と式 $(2)$ を合体した、

$$\frac{PV}{T}=一定\tag{5}$$

は、ボイル・シャルルの法則と呼ばれています。図示すると、

図３

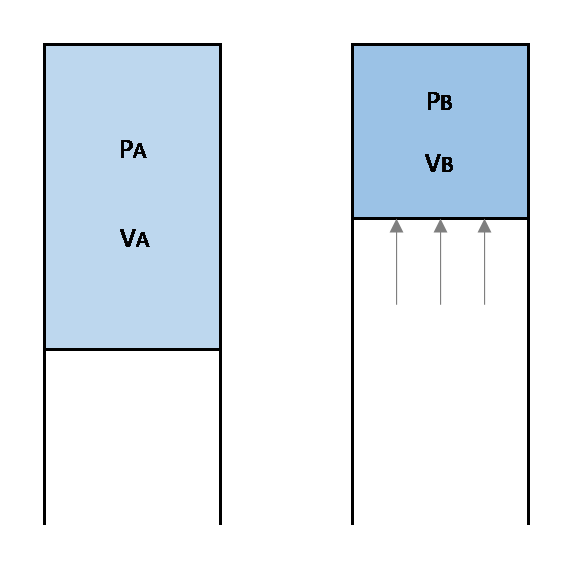
ボイルの法則 $PV=一定$。$T$ が一定のとき、$P_{A}V_{A}=P_{B}V_{B}$ が成り立つ。

図４

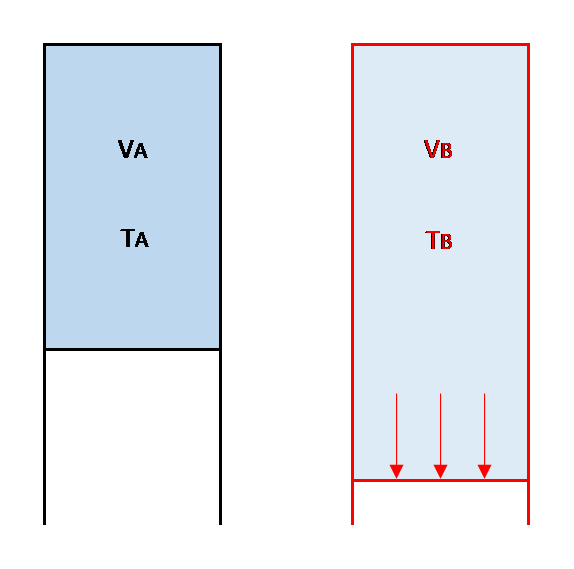
シャルルの法則 $\frac{V}{T}=一定$。$P$ が一定のとき、$\frac{V_{A}}{T_{A}}=\frac{V_{B}}{T_{B}}$ が成り立つ。

 

以上より、自然と人間の社会は、

	P	V	T
自然	気体の圧力	気体の体積	気体の温度
人間の社会	組織の圧力	組織の活力	組織構成員の待遇

 

のように対応していて、三つの変数のうち、ふたつが決まるともうひとつが自動的に決まるという、

$$\frac{PV}{T}=一定\tag{5}$$

の関係にあることがわかります。おもしろいですね。

以上

 

記事一覧へ戻る