年が明けましたので、恒例の日経平均終値予測をしましょう。

1950年から昨年2021年までの72年間の株価の推移をチャート（図1）で概観します。縦軸が対数であることにご注意ください。

図1

Nikkei 225 Index – 67 Year Historical Chart | MacroTrends より

 

ステップ１）

72年間の株価の日次変化率に注目し、上昇した日数と下降した日数、それぞれの変化率を以下の四つのパターンに分類します。

パターンA：　上昇した日数＞下降した日数、上昇率＞下降率

パターンB：　上昇した日数＞下降した日数、上昇率＜下降率

パターンC：　上昇した日数＜下降した日数、上昇率＞下降率

パターンD：　上昇した日数＜下降した日数、上昇率＜下降率

表１は過去72年間の変化を四つのパターン別に分類したものです。

表１　過去72年間の発現パターン分類

パターン	発現回数	平均上昇率	平均下降率	平均上昇日数	平均下降日数
A	23	0.748%	-0.680%	134	114
B	24	0.815%	-0.886%	132	106
C	19	0.905%	-0.843%	122	127
D	6	1.154%	-1.195%	118	129
	72

 

ステップ２）

次に、株価予測の公式を使ってパターン別に2022年末に到達する株価を計算します。

<$n$日後の株価 $x_{0}$を予測する公式>

$$x_{n}=x_{0}\ (1 + a)^p(1 − b)^q$$

$$(p + q = n,  a, b > 0)$$

$x_{0}$ は初期値。2022年の終値の予測であれば、初期値を2021年の終値の値である28,791.71円とします。$a$ は平均上昇率、$b$ は平均下降率、$p$ は上昇した日数、$q$ は下降した日数です。

 

「株価予測の公式」の導出については、「一年後の株価はどの程度の精度で予測できるか？」をご覧ください。

 

表１のデータを使って計算した結果が表２です。たとえば、来年もパターンAである確率は40.9%あって、その場合の終値は35,910.72円（前年比24.7%の増加）ということです。

表２　予測公式を使って予測した2022年の終値

移行パターン	出現回数	出現確率	2022年終値予測	増減率
A → A	9	40.9%	35,910.72	24.7%
A → B	6	27.3%	32,718.70	13.6%
A → C	6	27.3%	29,268.90	1.7%
A → D	1	4.5%	23,738.44	-17.6%
	22	100.0%

 

ステップ３）

最後に、上記の予測値をもうひとつの計算方法で得られる確率分布と照合します。株価は指数関数的に増えようとする一方で、必ず上下にゆらぎます。それを数式で表すと、

$$\frac{dx}{dt}=rx+vx\frac{dB(t)}{dt}$$

となります。$x$ が株価、$r$ は成長係数、$v$ はゆらぎ係数、$B(t)$ は日々のランダムな変化です。この式が株価 $x$ の瞬間、瞬間の変化を表しています。その積み重ねが株価の軌跡（図0のチャート）となります。上記の式は確率微分方程式と呼ばれ、その積み重ねを計算することを微分方程式を解く（積分する）といいます。その結果が、

$$x=x_{0}\ e^{(r-\frac{v^2}{2})t+vB(t)}$$

です。時間が t だけ経過したときに株価がいくらになるかを教えてくれる式です（導出方法は 2023年1月23日付けブログをご覧ください）。$x_{0}$ は初期値。$ｒ$（成長係数）、 $v$（ ゆらぎ係数）、$B(t)$（日々の変化）  の決め方は2020年4月21日付のブログ「コロナ・ショックによる株価下落の回復はいつか？」をご覧ください。すべてエクセルで計算できます。

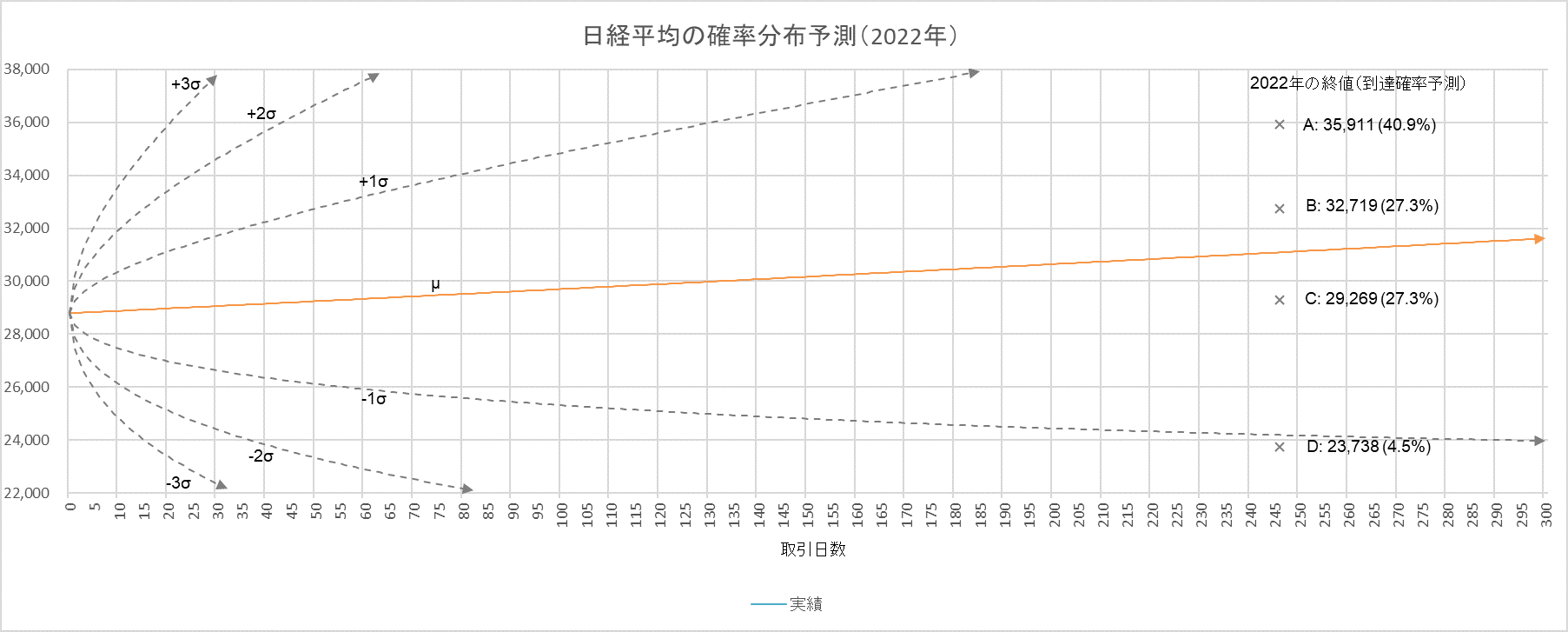
初期値を2020年の終値としたとき、株価が確率的にどう分布するかを示すのが図４です。オレンジの線 $µ$ を中心に、破線で示した $+1v、-1v、+2v、-2v・・・$が確率分布で、数値が大きくなるにつれてその範囲に入る確率は低くなります。そしてここに、上で求めた四つの予測値を重ね合わせます。おおよそ$\pm 1v$の範囲に収まっており矛盾がないことが分ります。

図2　日経平均の確率分布と2022年末の終値予測

 

予測計算は以上のとおりです。本年も週一回のペースで実際の日経平均と予測を照合します！

以上

記事一覧へ戻る