「勝ち癖」「負け癖」の数理的解釈
あなたはこれまで、ひとつのプロジェクトで成功をおさめ、もうひとつのプロジェクトは失敗に終わっています。さて、次のプロジェクトが成功する確率は何パーセントでしょうか?質問自体は極めてシンプルですが、それに答えるのは簡単ではありません。三つ目のプロジェクトの成功確率は五割でしょうか?いや、それ以下の可能性もあるし、それ以上の可能性もありますね。成功の可能性は0%から100%まで、まんべんなくありそうです。
ここで、三つ目のプロジェクトが成功だったとします。成功が二回、失敗が一回になりました。では、四つ目のプロジェクトが成功する可能性は何パーセントでしょうか?ここまでの成功率は三分の二(約67%)ですから、次のプロジェクトが成功する可能性も 67% といえるでしょうか?いえ、そうとは言い切れませんね。成功の可能性はこれまで同様、0%から100%まで残されています。ただ、三回の内二回は成功したわけですから、次に成功する可能性は0~100%の間にまんべんなくあるわけではなく、もう少し成功の方へ偏ってもおかしくありません。成功するかしないかを正確に言い当てることはできませんが、「成功の偏り」くらいならわかりそうです。
まずは、成功でもない、失敗でもないという中途半端な結果が生じないように、「成功」を定義づけしてください。そうすれば、成功する確率が $p$ なら、失敗する確率は $1-p$ と決まります。次に、成功したら $p$ に $p$ を、失敗したら $(1-p)$ に $(1-p)$ を掛け合わせます。つまり、$p^m(1-p)^n$ という形にします。右肩に載っている指数 $m$ と $n$ はスタート時はゼロにします。$p$ の値にかかわらず $0$ 乗したら “1” ですから、スタート時点では、成功する可能性は一様に “1” であることが表現できます(図1)。以降は、$p$ の右肩に成功した回数を、$(1-p)$ の右肩に失敗した回数を累積していきます。
<プロジェクトの成功と失敗の推移>
スタート地点: $p^0(1-p)^0=1.0$ (成功一回、失敗一回)
三回目のプロジェクト:成功 $p^1(1-p)^0=p$ (成功二回、失敗一回)
四回目のプロジェクト:成功 $p^2(1-p)^0=p^2$ (成功三回、失敗一回)
五回目のプロジェクト:成功 $p^3(1-p)^0=p^3$ (成功四回、失敗一回)
六回目のプロジェクト:失敗 $p^3(1-p)^1=p^3(1-p)$ (成功四回、失敗二回)
七回目のプロジェクト:成功 $p^4(1-p)^1=p^4(1-p)$ (成功五回、失敗二回)
・
・
・
$α+β$ 回目のプロジェクト $p^{α-1}(1-p)^{β-1}$ (成功 $α$ 回、失敗 $β$ 回)
以上を $p$ の関数と捉えて、
$$f(p)=p^{α-1}(1-p)^{β-1}\tag{1}$$
とします。$p$ は成功する確率ですから、$0$ から $1$ の値をとります。これが、関数 $f(p)$ をグラフにしたときの横軸になります。関数は上の経緯をみると $p$ の一次式、二次式、三次式・・・になっていますから、グラフは直線や曲線になりそうです。成功確率が p なら失敗確率がおのずと 1-p と決まるように、起こりうるすべての事象の確率を足し合わせると必ず $1$ になるのが確率のもうひとつのすっきりとした特長です。つまり、横軸とグラフ線に囲まれた面積を $1$ にすれば、それが「確率の分布」だとみなせます。式$(1)$ の面積を $1$ にするために定数 $C$ を導入すると、関数 $f(p)$ は、
$$f(p)=Cp^{α-1}(1-p)^{β-1}\tag{2}$$
となります。$C$ の求め方は(註1)をご覧ください。$α$ は成功回数、$β$ は失敗回数です。では、上記の成功と失敗の推移に合わせて、確率分布の変化をグラフでみていきます。
図1 図2
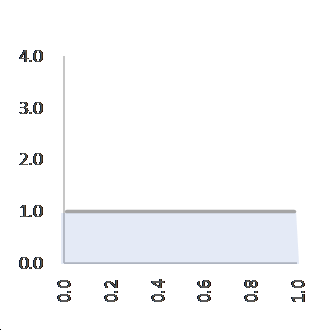
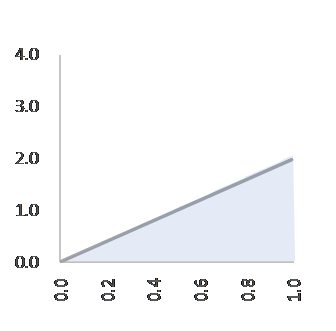
C=1, α=1, β=1, f(p)=1 C=2, α=2, β=1, f(p)=2p
成功一回、失敗一回のスタート時点の成功確率は一様に分布しています(図1)。
三回目のプロジェクト=成功。確率分布は右肩上がりの直線になりました(図2)。
図3 図4
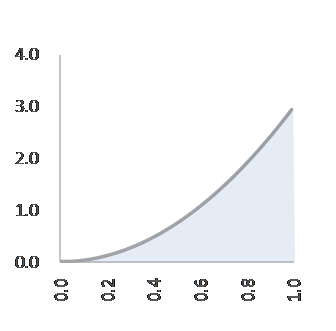
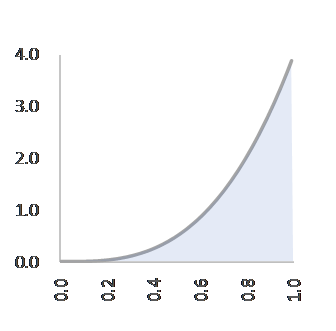
C=3, α=3, β=1, f(p)=3p2 C=4, α=4, β=1, f(p)=4p3
四回目と五回目のプロジェクト=いずれも成功。確率分布は右肩上がりの指数曲線に変化しています。
図5 図6
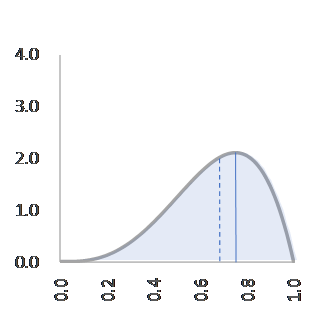
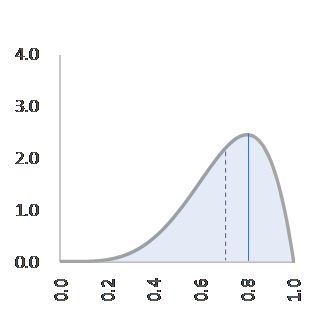
C=20, α=4, β=2, f(p)=20p3(1-p) C=30, α=5, β=2,f(p)=30p4(1-p)
六回目のプロジェクト=失敗。確率分布が変化し、 p=0.75 で最大になっています。成功率(破線)は 0.67 です(図5)。
七回目のプロジェクト=成功。確率分布は少し右へ偏りました。分布は p=0.80 で最大に、成功率は 0.71 です(図6)。
図 7 は図 6 の $p=0.5$ 以上の面積を示したものです。面積は積分 $\int_{0.5}^{1.0}30p^4(1-p)dp$ でも、エクセルのベータ関数 でも求めることができ、$0.89$ です。つまりこの時点でプロジェクトが五割以上成功する確率はほぼ九割だということです。新しいプロジェクトに挑戦するときはいつも不安がともなうものですが、漠然と「これまで成功した回数の方が多いから、次も成功する確率が高い」と思うのと、「次のプロジェクトが五割以上成功する可能性は九割」、「最も起こりやすい成功確率は八割」、とわかっているのでは、心強さが違いませんか?「勝ち癖」には数理的な裏付けがある、ということですから自信をもってチャレンジしてください!
図7
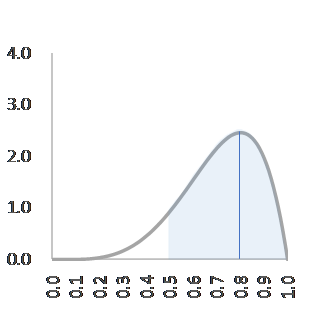
f(p)=30p4(1-p)
プロジェクトが五割以上成功する確率(p=0.5以上の面積)は 89% 。
逆に失敗の回数が成功回数よりも多い「負け癖」パターンは以下のとおりです。「勝ち癖」パターンの左右対称形になっているのがわかります。
図8 図9
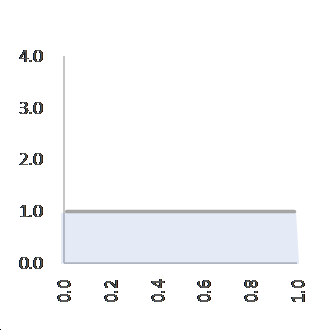
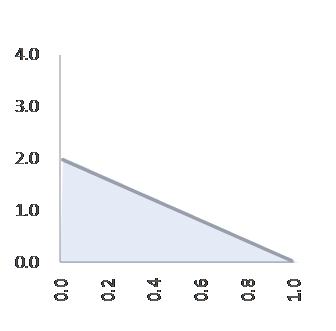
C=1, α=1, β=1, f(p)=1 C=2, α=1, β=2, f(p)=2(1-p)
図10 図11
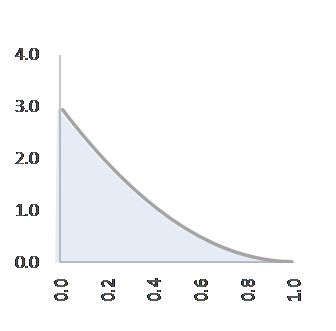
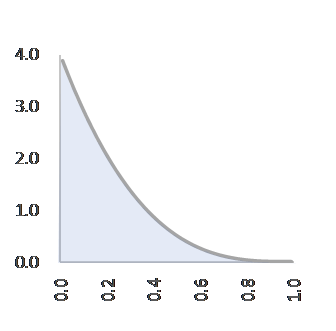
C=3, α=1, β=3, f(p)=3(1-p)2 C=4, α=1, β=4, f(p)=(1-p)3
図12 図13
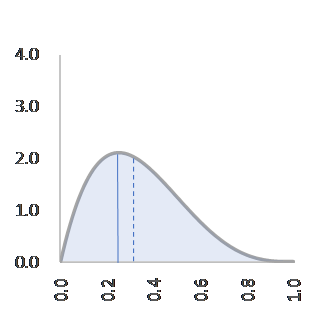
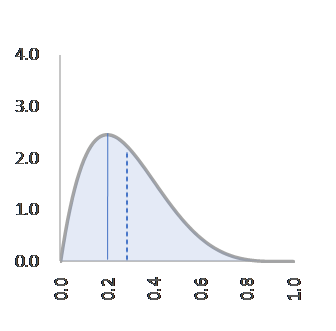
C=20, α=2, β=3, f(p)=20p(1-p)2 成功最尤率0.25<成功率0.33 C=30, α=2, β=4, f(p)=30p(1-p)3 成功最尤率0.20<成功率0.29
以上の結果を一覧表にすると、
| 図13 | 図12 | 図5 | 図6 | |||
| 成功数 $α$ | 2 | 2 | 2 | 4 | 5 | 6 |
| 失敗数 $β$ | 6 | 5 | 4 | 2 | 2 | 2 |
| 成功率 | 0.25 | 0.29 | 0.33 | 0.67 | 0.71 | 0.75 |
| 成功最尤率 | 0.17 | 0.20 | 0.25 | 0.75 | 0.80 | 0.83 |
| 五割以上の成功確率 | 0.06 | 0.11 | 0.19 | 0.81 | 0.89 | 0.94 |
となります。
(註1)$C=\frac{(α+β-1)!}{(α-1)!(β-1)!} (α>1, β>1) $ で、確率分布の面積を 1 にするための規格化定数です。
(註2)成功最尤率 = $\frac{α-1}{α+β-2}(α>1, β>1) $ で、$0$ から $1$ に横たわる $p$ のなかで「最も尤もらしい=起こりやすい確率 $p$ 」です。
おわり
記事一覧へ戻る