2020年も本日が最終日。昨日の日経平均の終値は27,444.17で平成バブル崩壊後の最高値を更新していますが、本日は社会経済環境を切り離して、単純に数学的な確率を使って日経平均が再現できるかどうかに挑戦します。ここで設定する仮説はシンプルに以下とします。

• 株価は絶えず指数関数的に増加しようとしている。
• 翌日の株価は前日の株価に対して絶えずランダムに変化する。

さて、このふたつの条件だけで、日経平均の実際の動きを再現できるでしょうか。計算の仕方は以下のとおりです。（具体的な計算方法は別紙の「エクセル関数で作り出した日経平均」を参照してください。）

• 初期値を2010年1月4日の日経平均終値とします。
• 指数増加係数を 2.94 x 10^-4/日とします。
• 株価のランダムの変化はエクセル関数NORMINV(RAND(),0,0.6)（平均 0、標準偏差 0.6 で正規分布する値を返す）から導きます。

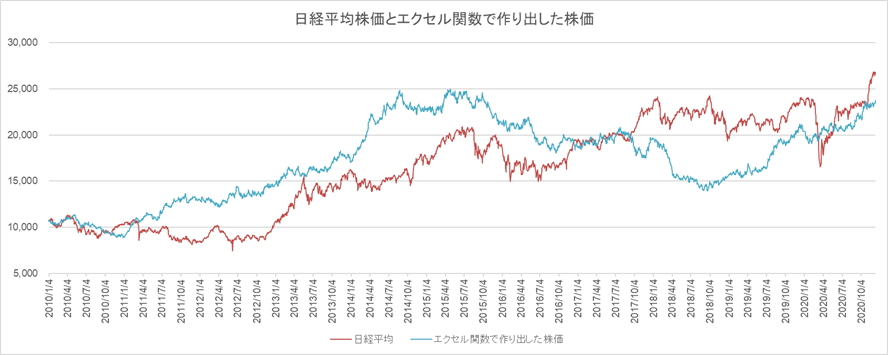
以上をグラフ化すると、とたえば下図のようになります。

図1

初期値=10,654.79 (2010/1/4)、増加率=2.94×10^-4/日、株価のランダム変化率=NORMINV(RAND(),0,0.6)

 

赤線が実際の日経平均、青線がエクセルで作り出した株価です。ランダム関数が入っていますので、青線はもちろん確定しているわけではなく、さまざまに変化します（添付のエクセルでF9ボタンを何度も押してください！）。図1は実績を下回っていますが、図2のように実績を上回るパターンが出てみたり、

図2

初期値=10,654.79 (2010/1/4)、増加率=2.94×10^-4/日、株価のランダム変化率=NORMINV(RAND(),0,0.6)

 

図3のように途中から実績を下回るパターンなど、ありとあらゆるパターンが出現します。

図3

初期値=10,654.79 (2010/1/4)、指数増加率=2.94×10^-4/日、株価のランダム変化率=NORMINV(RAND(),0,0.6)

 

そして、何度も試行していると実績の赤線にかなり近いものも現れます。たとえば、図4あたりになってくるとかなり実績に近いですね。

図4

初期値=10,654.79 (2010/1/4)、指数増加率=2.94×10^-4/日、株価のランダム変化率=NORMINV(RAND(),0,0.6)

 

数十回の試行でこれだけ近いものが出現するということであれば、数千回、数万回、と試行を繰り返すとさらに実績に近いものも現れるはずです。

さて、以下のチャートは1971年以降の日経平均株価（年次終値）で、その時々の景気と社会イベントが書き込まれています。これをみると三菱地所がニューヨークのロックフェラー・センターを買収した平成バブルをなつかしく思い出したり、バブル崩壊後の「失われた20年」という言葉を思い浮かべたりするひともいるでしょう。

図5

1971年以降の日経平均の推移と社会イベント

 

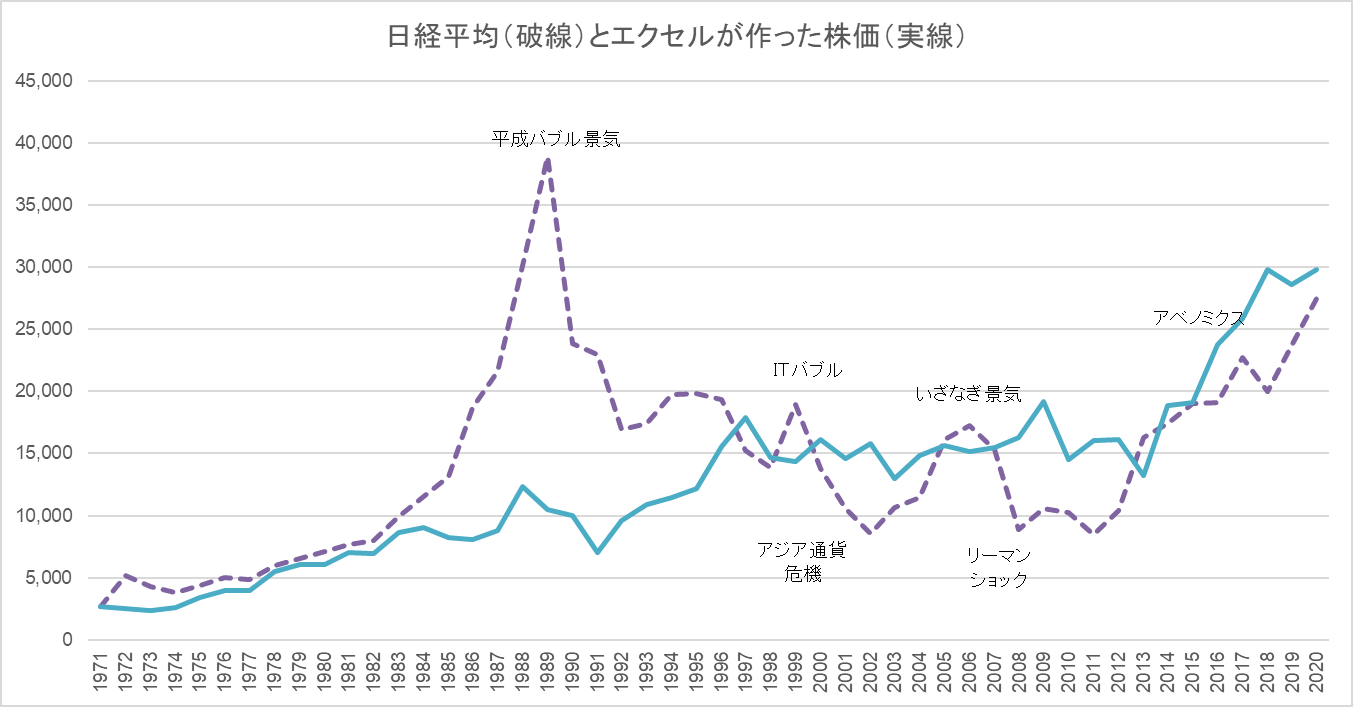
さて、ここでエクセルのF9ボタンを何度も押してみます。すると、平成バブルもリーマンショックもなく、順当に成長するパターン（図6）や、

図6

平成バブルもリーマンショックもなかった場合

 

平成バブルがもう少しあとで発生するパターン（図7）、

図7

平成バブルが遅れてやってきた場合

 

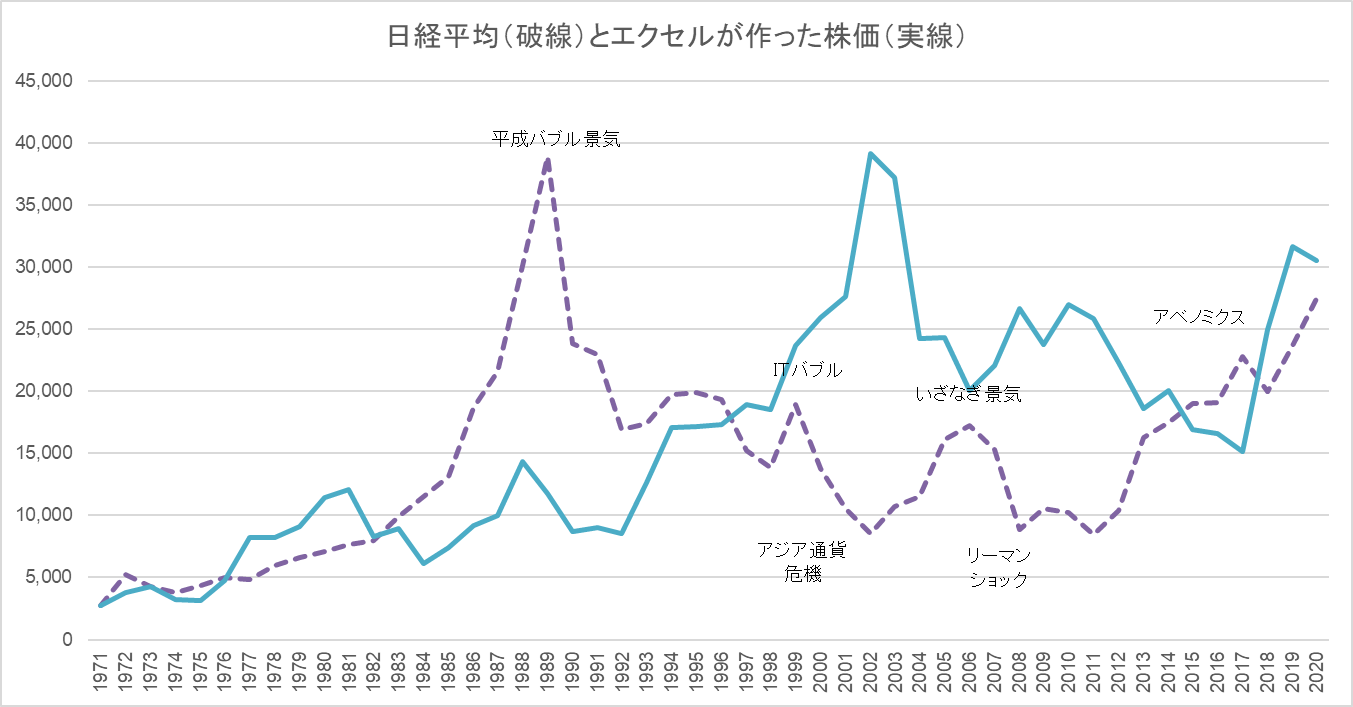
あるいは、同じようなタイミングで平成バブルが来て、逆リーマンショック（第二の平成バブル）がやってくるパターン（図8）も現れます。

図8

第二の平成バブル（逆リーマンショック）がやってきた場合

 

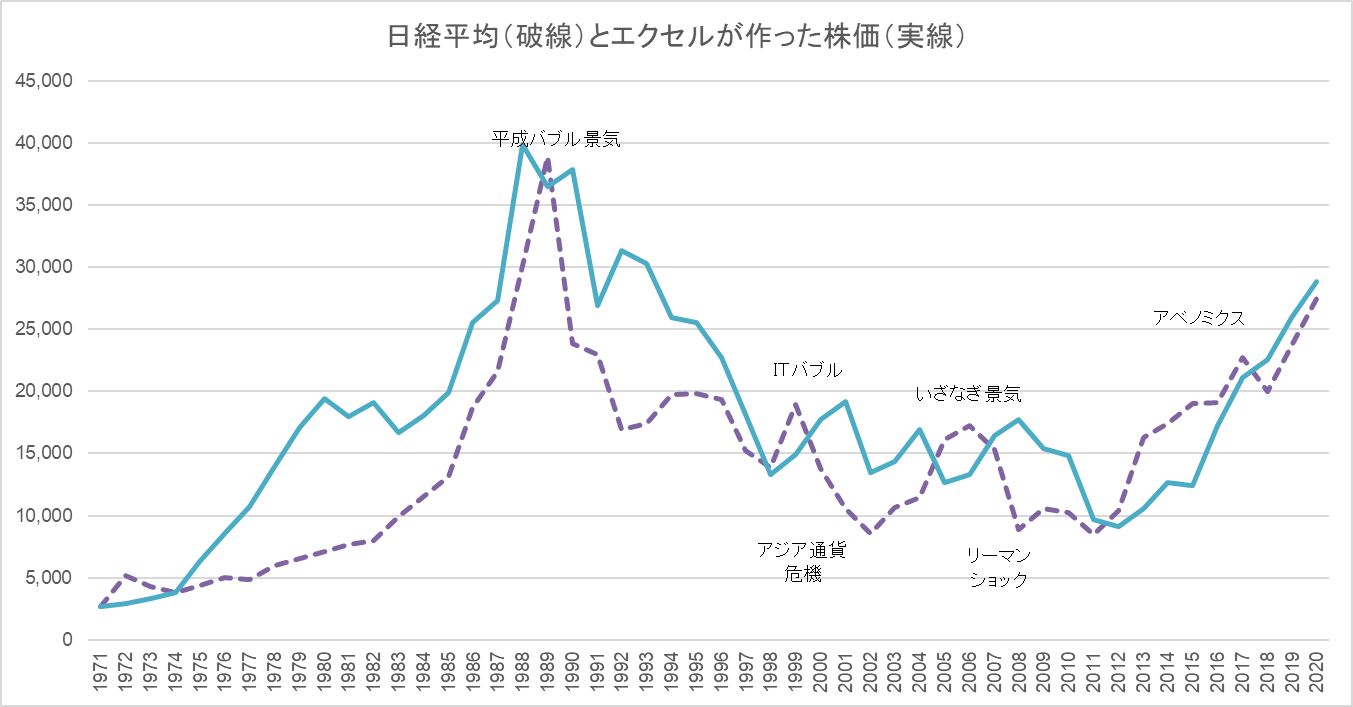
そして、平成バブルも、リーマンショックも、アベノミクスも同じようなタイミングで登場させたいのであれば、それもできます（図9）。

図9

平成バブルもリーマンショックも、アベノミクスも現れるパターン

 

これらのことから何が分かるでしょうか？

何とか景気、何とかショック、などと呼ばれると、そのときどきの株価の動きはあたかもそれが「必然」であったかのように思えてしまいます。しかしながら、それらは必然ではなく「偶然」だったとしても何らおかしくありません。なぜなら、乱数を使って似たような動きを再現することができるからです。そして、社会イベントの命名も後付けで行われているに過ぎず、もし違う動きをしていたならまたそれらしい別の名前が付いていたと考えることもできます。これは日経平均だけにいえることではなく他のいかなる株価においてもいえることです。是非下の「エクセル関数で作り出した日経平均」をクリックして体感してみてください！

以上

Excelはこちらから　→　エクセル関数で作り出した日経平均　

記事一覧へ戻る