その一 では、「株価はゆらぎながら指数関数増加する」という前提に立つと、そのチャートは N 字の繰り返しになるという説明をしました。最後に掲載した図4をみてください。

図4

N字成長するS&P500。チャートの頂（ピーク）と谷底（バレー）を $σ$曲線で結ぶとN字になる。$σ$曲線は確率微分方程式の解から計算で求めることができる。

 

それぞれの N 字の起点と終点がチャートの頂と谷底になっていることに注目してください。では、チャートをズームアップして2020年1月以降の動きをみてみましょう。図5をご覧ください。図4の右端の一本の$σ$線が、13本の$σ$線に細分されました。それでも N 字成長していることに変わりはありません。

図５

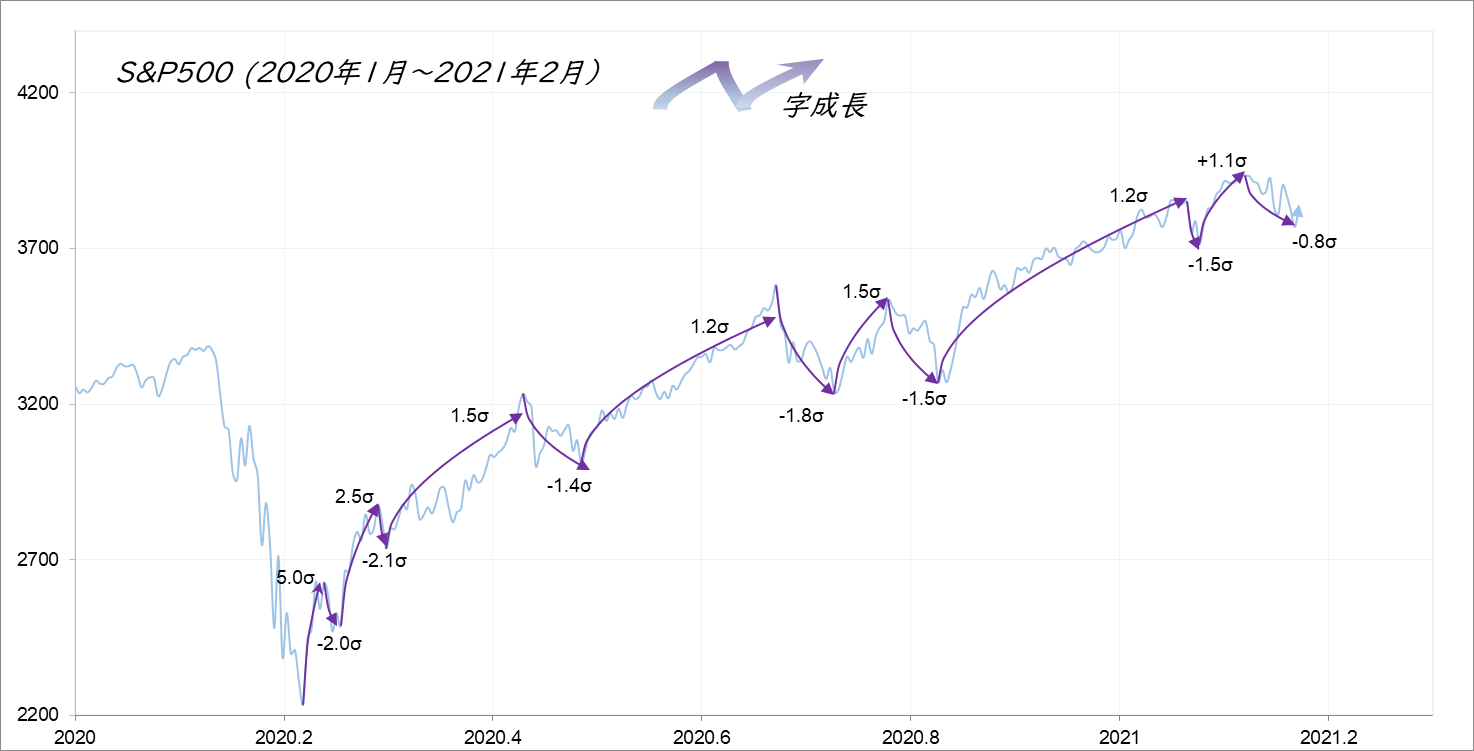
ズームアップしたS&P500。ここでもN字成長を繰り返していることが分る。

 

実は、株価チャートは月単位、週単位、日単位、一時間単位、15分単位、10分単位、5分単位、1分単位と細分化することができます。そのどれをとってもしっかりしたギザギザ模様となります。通常の図形であれば、細いところをズームアップしていくとだんだん大まかに、滑らかになっていきますが、株価はそうなりません。このようにどこまでいっても部分と全体が同じ図形（自己相似）のことをフラクタル図形と呼びます。身近な例としては海岸線やロマネスコなどがあります。

　

どこまで拡大してもギザギザがなくならない海岸線と同じ形のつぼみがらせん状に連なるロマネスコ（アブラナ科の野菜）

 

では、フラクタルが分かったところで、図5をさらにズームアップします。そうすると少し気になるところが出てきます。図６の丸印を付けた箇所 A と B をよくみると$σ$ 線が断層になっていてつながっていません。二か所に共通している点は株価がそれぞれの頂点に達したあとにストンと落ちていることです。最初の谷底までの落差は頂点Aからは7.1％、頂点Bからは9.6％もあります。

図６

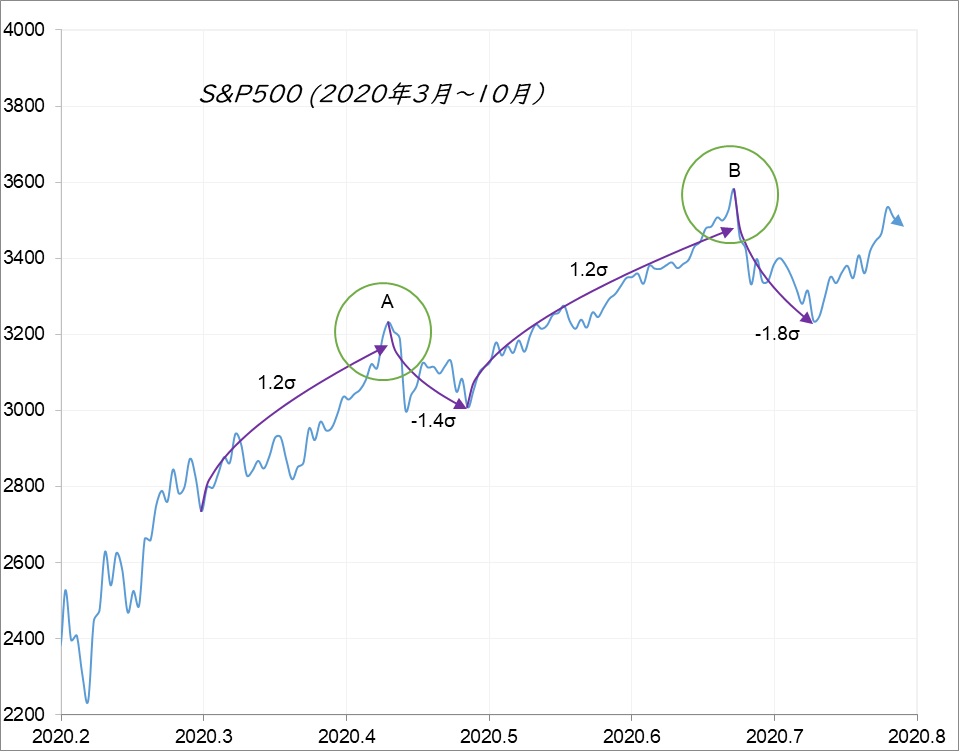
丸印の箇所で $σ$線がつながらず前後の株価をうまく近似できていない。AとBはいずれも頂点から谷底へ急降下している。最初谷底までの落差はAが7.1%、Bは9.6%。

 

ここで思い出すのが ディディエ・ソーネット 教授の対数周期曲線です。この曲線は株価が暴落する前に現れます。（詳細は2021年2月15日付のブログ「 株価暴落前の数学的兆候 ソーネット教授のドラゴン・キング理論（前編）」を参照してください。）通常、暴落というと二割～三割くらい下落しますので、上記のような一割未満の下落率では暴落とはいえませんが、この理論を借用して対数周期曲線を当てはめてみましょう。図７をご覧ください。

図７

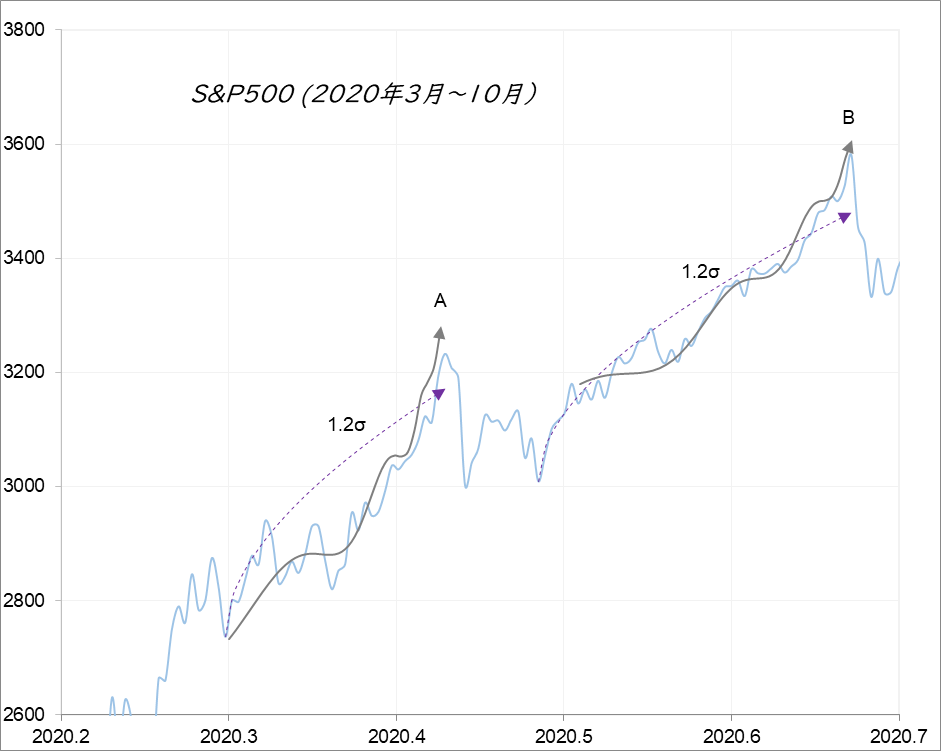
$σ$線でうまく近似できない箇所にディディエ・ソーネット教授の対数周期曲線（ドラゴン・キング理論）がフィットするとその先に急降下が待ち受けている。

 

$σ$線でうまく近似できなかった箇所に対数周期曲線が見事にはまります。対数周期曲線の先に待っているのが、ドラゴン・キング（＝バブル崩壊）というのがソーネット教授の理論ですが、ここではそこまでの大事には至らないということで、出てくるのはドラゴン・キングではなくリザード（とかげ）ということにしておきましょう。

ここまでで分かったことを整理すると、

①　株価は基本的には確率微分方程式から導かれる$σ$線にそって N 字成長する。

②　$σ$ 線で近似できない株価の動きには対数周期曲線を当てはめてみる。フィットすれば株価の急落が間近にせまっている可能性がある。

ソーネット教授がもしポケモンをご存知であれば、小規模な急降下はリザードの、バブルの崩壊はその進化形であるリザードンの仕業だと例えたかもわかりません（笑）。

　　

　　リザードとリザードン（右は巨大マックスの姿）ポケモン図鑑より

 

以上

 

記事一覧へ戻る