単純な微分方程式による予測

はじめに

厚生労働省の発表によると新型コロナ・ウィルスに対するPCR検査は2020年4月14日までに100,703人に対して行われ、陽性者数は8,582人（8.5%）に達している。死亡者は136人であるので陽性者の致死率は1.6%である。今後どこまで感染が拡がるのか、そしてそれはいつ収束するのか、につき生態学の数理モデルをつかった予測をおこなう。また、外出自粛と感染者数にどのような相関関係があるのか、ゴールデンウィーク明けまでとされる自粛期間は妥当なのか、についても数理的に検証する。

基礎理論

まだ病原体に感染していないがこれから感染する可能性のある人（以下単純に未感染者と呼ぶ）の数をx、感染していて他人にうつす可能性のある人（以下、感染者）の数をyとする。最も簡単な方程式は次のように与えられる（以下、方程式 ①）。

$$\frac{dx}{dt}=-bxy$$

$$\frac{dy}{dt}=bxy-cy$$

ここで $b$ は未感染者が感染者に出会って感染する率（以下、感染係数と呼ぶ）、$c$ は感染者が治癒するか死ぬかして感染者でなくなる率（以下、まとめて治癒係数と呼ぶ）を表している。ここで、感染者の変化率である $\frac{dy}{dt}$ がゼロとなる ${x = \frac{c}{b}} $に注目する。 未感染者の初期値を$x$₀とすると、$\frac{dy}{dt}$ は $x$₀ > $\frac{c}{b}$ であればプラスに、逆に$x$₀ < $\frac{c}{b}$ であればマイナスになる。つまり $x$₀ ＜ $\frac{c}{b}$ であれば感染者は増えない。以下に、感染係数 $b$、治癒係数 $c$、未感染者初期値 $x$₀ の違いが感染者数にどう影響するかを図示した。

図1-1                                                                  図1-2

   

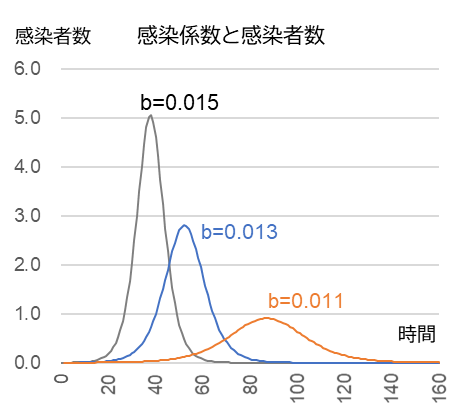
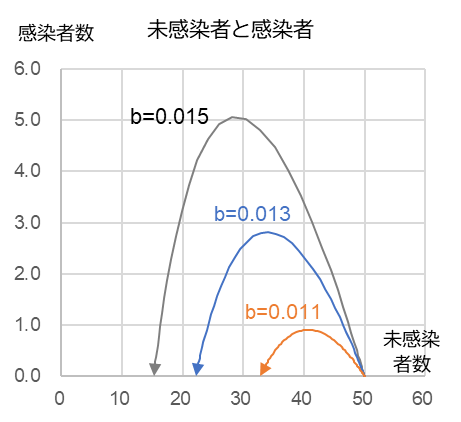
$c$ = 0.45, $x$₀ = 50, $y$₀ = 0.001 　

ピーク（単位は任意）$t$ = 38, 52, 86

ピーク時の未感染者数 ${x = \frac{c}{b}}$ = 30.0, 34.6, 40.9

ピーク時の感染者数 $y$ = 5.1, 2.8, 0.9 

図1-1 は感染係数の違いによる感染者数の時系列変化。感染者一人が未感染者のグループの中に入ったあとの伝染病の時間的な拡がりを示している。係数のわずかな違いで感染者数は大幅に変動する。感染係数が大きいと感染者数がピークに達するまでの時間も速い一方、収束する時間も短い。同係数が小さくなるにつれゆっくりと穏やかに感染者が増える一方で収束の速度も遅い。図1-2 は未感染者数（横軸）と感染者数（縦軸）の相関関係。未感染者とは感染する可能性のあるひとのことであるので、感染の拡大とともに減少する（一度獲得した免疫を失うことはないという前提）。感染者数の変化率は ${\frac{dy}{dt} = bxy-cy}$ なので、未感染者 $x$ が $\frac{c}{b}$ に達した時点で減少に転じる。

図2-1                                                                 図2-2

 

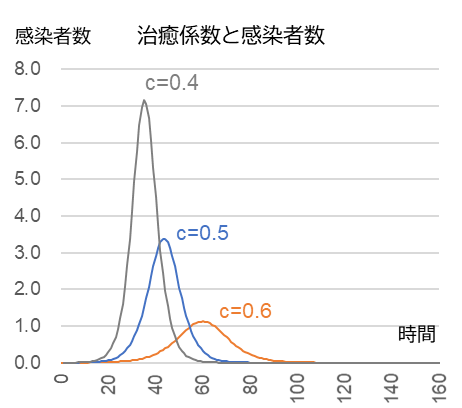
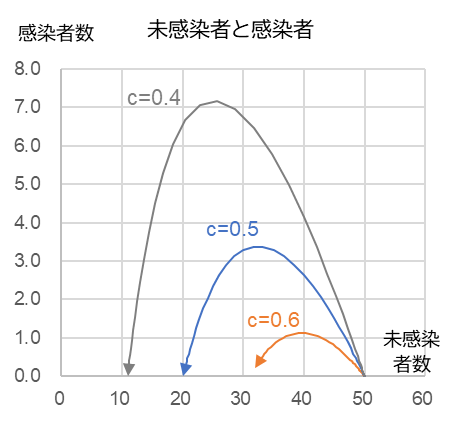
$b$ = 0.015, $x$₀ = 50, $y$_o = 0.001                        

ピーク（単位は任意）$t$ = 34, 42, 60　　　

ピーク時 ${x = \frac{c}{b}}$ = 26.7, 33.3, 40.0

ピーク時の感染者数 $y$ = 7.2, 3.4, 1.1

図2-1 は治癒係数 $c$ の違いによる感染者数の時系列変化。$c$ をワクチンの開発、投与率等によって上げることができれば感染者数は減少する。図2-2 は感染者数と未感染者数の相関関係。感染係数同様、感染者数が $\frac{c}{b}$ に到達すると減少に転じる。

図3-1　　　　　　　　　　　　　　　　図3-2

 

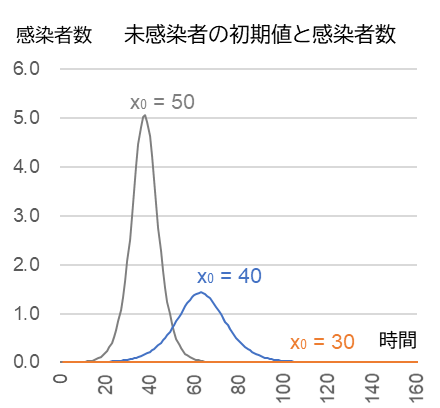
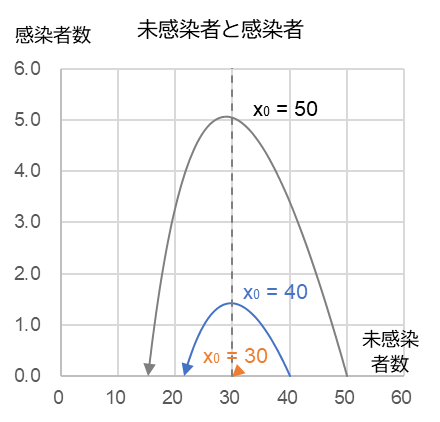
$b$ = 0.015, $c$= 0.45, $y$₀ = 0.001                   

ピーク（単位は任意）$t$ = 38, 62, 0　　　

ピーク時 $x$ = $\frac{c}{b}$ = 5.0, 1.4, 40.0

ピーク時の感染者数 $y$ = 5.1, 1.4, 0

図3-1 は未感染者の初期値の違いによる感染者数の時系列変化。図3-2 は感染者数と未感染者数の相関関係。未感染者の初期値 $x$₀ が $\frac{c}{b}$ = 30 以下であれば感染者は増えない。ワクチンを摂取して免疫をつけることは $x$_o を減少させるためだが、全員に摂取しなくても $x$₀ を $\frac{c}{b}$ より下げることができれば伝染病の流行を止めることができる。また、感染する可能性のないひとは ｘ には含まれないので、外出を自粛をすることは $x$₀ を下げることにつながる。

新型コロナ・ウィルス対策への応用

では、実際のデータを使って新型コロナ・ウィルスがいつ収束するか、また外出自粛がどの程度効果を発揮するのかを予測してみよう。データは厚生労働省のホームページ内の「新型コロナ・ウィルス感染症の国内発生動向（2020年4月14日掲載分」を使用した。

図4

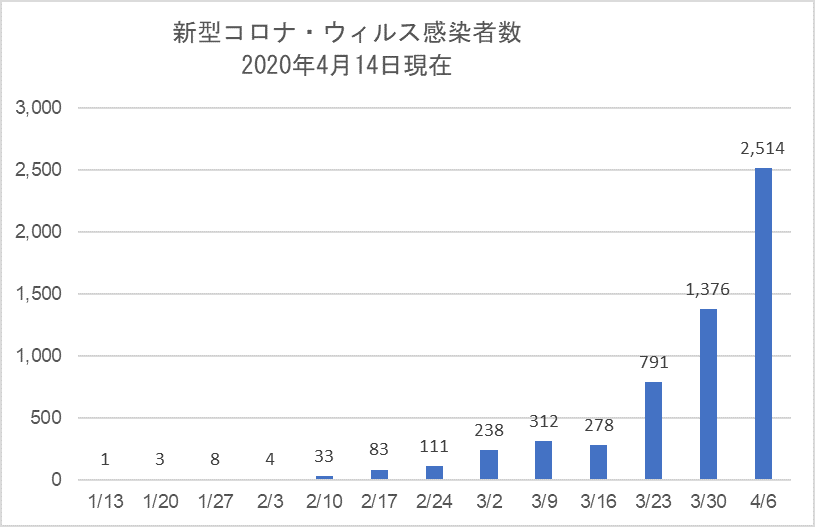
計算に必要な係数は伝染件数 $b$ と治癒係数 $c$、未感染者と感染者の初期値 $x$₀ と $y$₀ である。図5-1 は実データ、図5-2 は方程式 ①の解曲線である。このふたつを縦軸のスケールを揃えて重ね合わたものが図5-3である。

図5-1                                                      図5-2                          

   

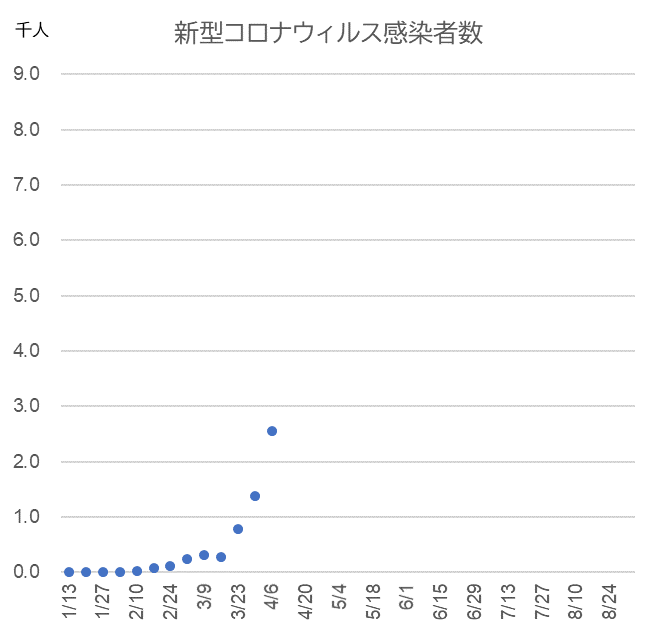
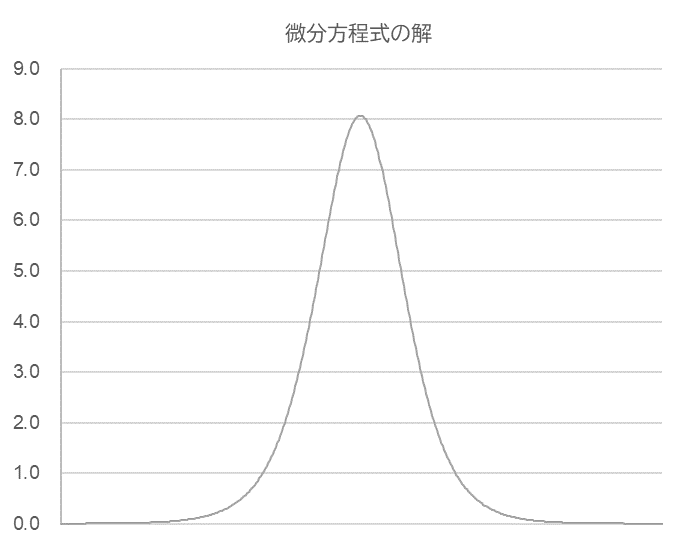
図5-3

$b$ = 0.015, $c$ = 0.45, $x$₀ = 50, $y$₀ = 0.001

ここで、治癒係数 $c$ を 0.45 に固定して、伝染係数 $b$ を 0.015 → 0.013 → 0.011 と変化させてピーク時の感染者数、時期を比較してみよう。図6 は実データを伝染係数 $b$ = 0.015 の解曲線にフィッティングした様子。4月第4週以降にピークを迎え、週間感染者数は 5千人に達する。

図6

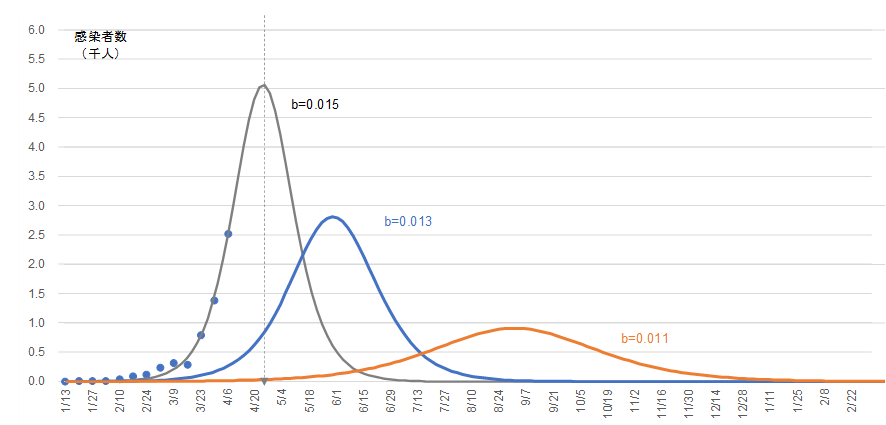
$b$ = 0.015, $c$ = 0.45, $x$₀ =5 0, $y$₀ = 0.001

ピーク時の感染者数 ≒ 5千人/週

ピークに達する時期：4月最終週～5月の第一週

感染係数を 0.013 に落としてみると、ピークの到来時期は $c$ = 0.015のときと変わらないが、感染者数が減少する（図7）。

図7

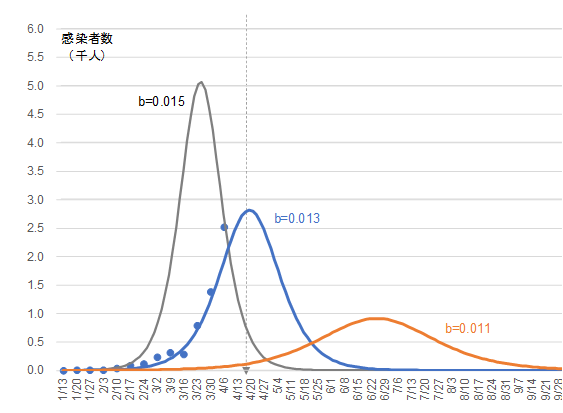
$b$ = 0.013, $c$ = 0.45, $x$₀ = 50, $y$₀ = 0.001

ピーク時の感染者数 ≒ 2.8千人/週

ピークに達する時期：4月第3～4週

伝染係数を仮に $b$ = 0.011 に落としてみるとフィッティングできない（図8）。よって、治癒係数 $c$ = 0.45 という前提のもとでは感染のピークはおおよそ四月末から五月に到来すると予測できる。

図8

$b$ = 0.011, $c$ = 0.45, $x$₀ = 50, $y$₀ = 0.001

次に治癒係数 $c$ の変化にともなう感染者数の動向をみてみよう。治癒係数 $c$ の変化も伝染係数 $b$ とほぼ同様の感染動向を示す。図9 が伝染係数を $b$ = 0.015 に固定して治癒係数を $c$ = 0.45 → 0.5 → 0.55へ上げたときの変移。

図9

$b$ = 0.015, $x$₀ = 50, $y$₀ = 0.001

ピーク時の感染者数 ≒ 3～5千人/週

ピークに達する時期：4月下旬～5月上旬

治癒率が上がるというのは、たとえば新型コロナ・ウィルスに適した既存の薬が見つかったり、あたらしい治癒薬が開発されたりすることに相当する。新型の感染症は事前予測ができないことから感染がはじまったあとに治癒係数が変化する（上がる）というのが現実的なパターンであろう。その場合、感染のピーク時期や感染者数がどう変化するだろうか。

図10 は治癒係数 $c$ が 0.45 と一定の場合と 0.45 から 0.55 へ上昇した場合、0.45 から 0.65 へ上昇した場合を示している。感染のピーク時期が前倒しになるとともにピーク時の感染者数も四割～五割減少することがわかる。

図10

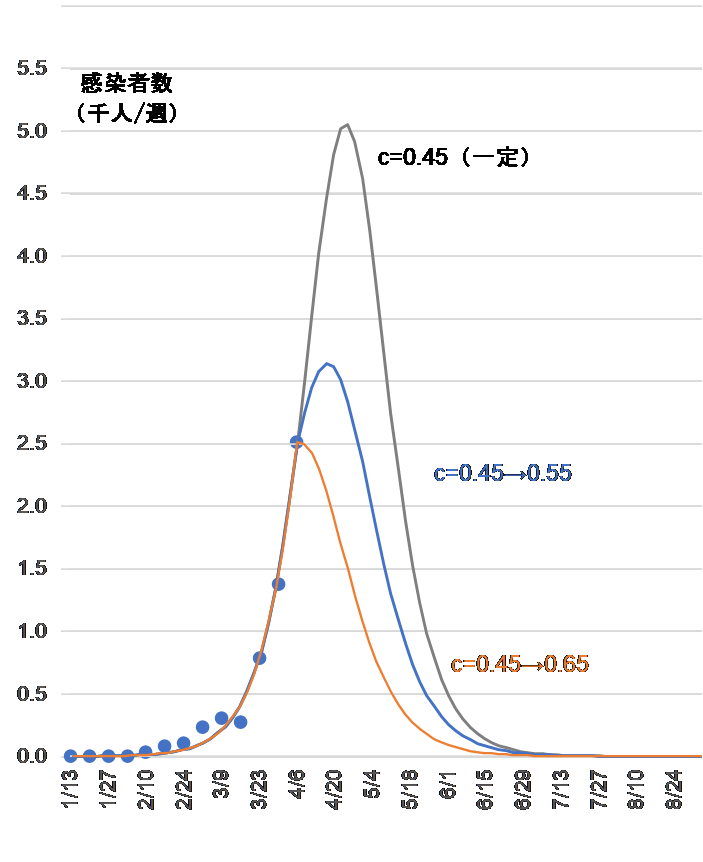
 $b$ = 0.015, $x$₀ = 50, $y$₀ = 0.001

もし、有効な治癒薬や治療法の開発が難しい場合、残る手段は感染する可能性のあるひとの数 $x$ を減らすということだけになる。$x$ の値を流行の兆しが見えた段階で、外出自粛、ひとが集まる場所の閉鎖、イベントの活動停止、ロックアウト（都市封鎖）などによって急激に減らすことができた場合の感染者数の推移を試算したのが 図11 である。感染可能者数が四割減った場合と八割減った場合を示した。いずれも感染の拡大は止まり感染者数が減少していく。八割も減らすことに成功すれば感染者数は一ヵ月程度でゼロに近づくことがわかる。

以上より、治療法の確立が間に合わない今回のようなケースは各人が感染を避ける行動をとることしか防御策がない。しかしながら、それは治癒率を上げることよりも即効性があり最も有効な感染防止策であることがわかる（図11）。一時的な経済的損失は避けられないが政府が雇用の安定を補償するなどしてひとの接触を減らすことが新型コロナ・ウィルスを早期克服する特効薬であると結論できる。

図11

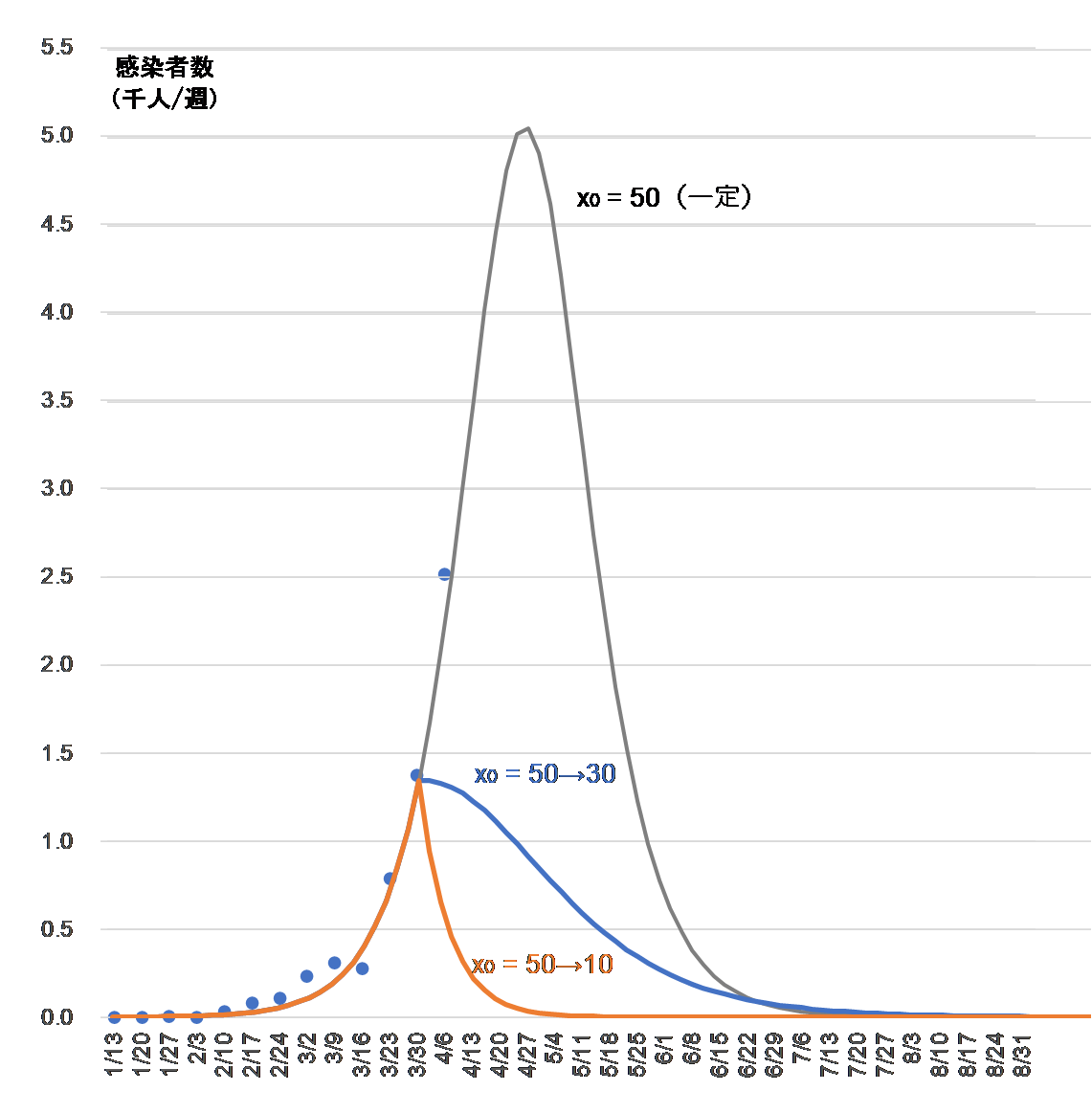
 $b$ = 0.015, $c$ = 0.45, $y$₀ = 0.001

感染可能者数を減らすことで感染拡大は停止し、その後感染者数は急激に減少する。図10 と比較すると治癒率の上昇よりも感染可能者の数を減らすことの方が即効性があることがわかる。

最後に

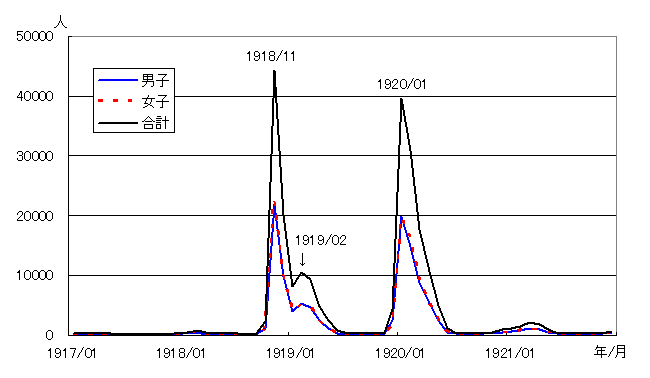
ここで使用した方程式は、生物学でよく使われる「捕食者とその餌となる生物の量の関係」をモデル化したもの（ロトカ・ボルテラ捕食系）の応用版である。捕食者がウィルスに感染したひと、餌をウィルスに感染する可能性のあるひと、とすれば同じモデルを適用することができる。図12は今から100年前に大流行したスペイン風邪による日本国内の死亡者数の推移（東京都健康安全研究センターの研究データ）である。流行期間は1918年8月から1921年7月でピークが三回訪れた。一回目の感染者は21.2百万人、死亡者数は25.7万人、二回目は2.4百万人が感染し、12.8万人が死亡、三回目は22.4万人が感染し、3.7千人が死亡した。いずれの曲線もモデルで得られる曲線とほぼ同じ形をしていることに注目したい。

図12

新型コロナ・ウィルスの感染者数や死亡者数は厚生労働省から毎日公表されているので、今後の推移を予測曲線と照合し、前提条件やパラメーターの妥当性等を検証していきたい。

以上

 

＜追記・修正＞

2021年6月18日に、図9、図10に関する説明文の一部を修正しました。

2021年6月19日に、計算の詳細 伝染病の流行 – Excel を追加しました。

 

記事一覧へ戻る