日々発表されるデータを予測に活かす方法

 

2022年4月2日付のブログ「次のプロジェクトが成功する確率」で、実際に起こった成功と失敗をつど更新することで次に起こる事象の確率が少しずつ見えてくるという話をしました。成功する確率を $p$ とすれば、失敗する確率は、$1-p$ なので、規格化定数を $C$ とすれば、成功の確率分布は $p$ の関数として、　

$$f(p)=Cp^{α-1}(1-p)^{β-1}\tag{1}$$　　　

と書けることを示しました。$α$ は成功回数、$β$ は失敗回数です。図1 は、$α=5$、$β=2$ 、図2 は、$α=25$、$β=10$ を式 $(1)$ へ代入して、面積が $1$ になるように規格化したグラフです。

図1                                                                                    図2

　　　

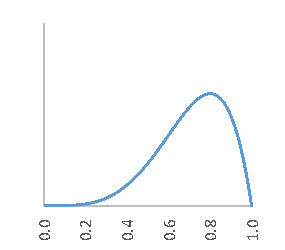
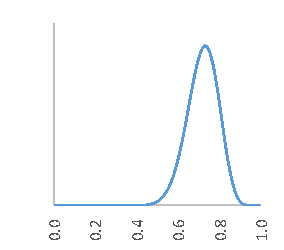
f(p)=C*p⁴(1-p)　　　　　　                                           　　　f(p)=C*p²⁴(1-p)⁹

成功 5回、失敗 2回　　　　　　　        　　　　　成功25回、失敗10回

 

成功と失敗の比率は、5:2 = 25:10 で同じですが、図2の方がスリムになっているのがわかります。図1では、0.5 以下の可能性もまだ 10% くらい残っていましたが、図2ではほぼ 0% 。成功率が同じ五分の二（約71%）であっても、「ここまで25回も成功したのだから、次の成功に対する確信度は5回しか成功していないときに比べると大きいはずだ！」という直感にも合致します。

このように実際に起こった新しい事象やデータを積み重ねていくと予測精度が少しずつ上がっていく（であろう）例はほかにもあります。

図3は、2021年の日経平均の日次終値の散布図、図4はそれをヒストグラムにしたもので、正規分布に近い形をしているのが分かります。

図3                                                                                     

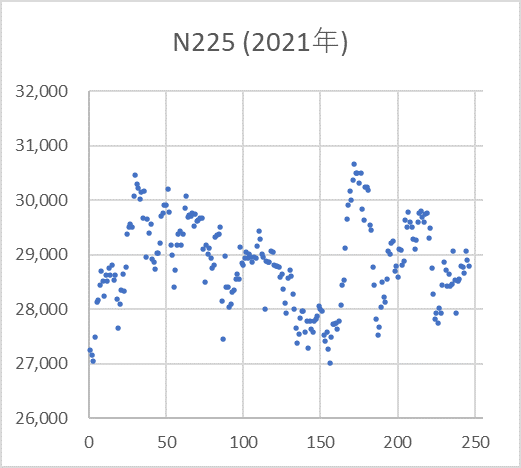
2021年 日経平均日次終値の散布図（横軸は取引日数）

図4

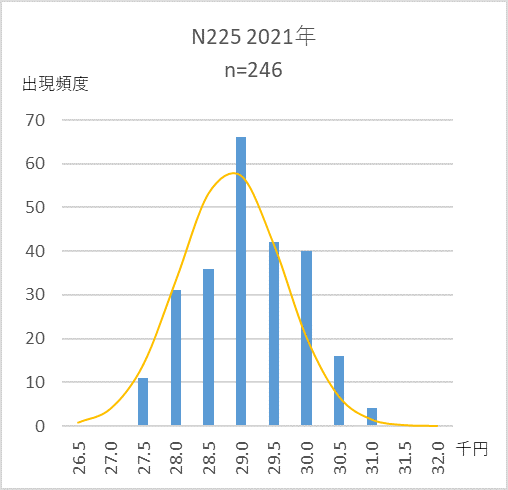
2021年 日経平均日次終値のヒストグラムと正規分布曲線

 

ここで単純に、日経平均は任意の期間において正規分布に従うと仮定しましょう。試しに、2022年の取引開始日から20日間の終値の分布状況は図5のとおりでした。

図5

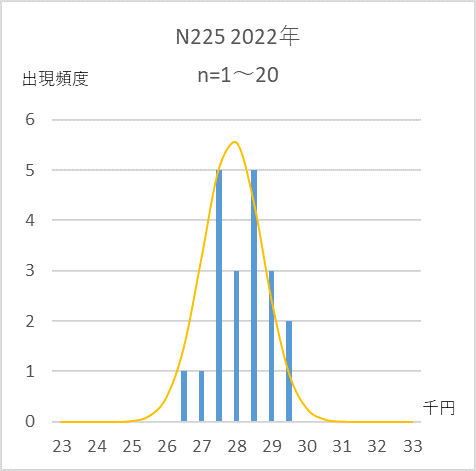
2022年 日経平均日次終値（1/4～2/1）のヒストグラムと正規分布曲線

 

おおよそ、正規分布しているようです。なぜ、正規分布にこだわるかといいますと、正規分布に正規分布を掛け合わせるとまた正規分布になるというおもしろい性質があるからです。掛け合わせてもいいなら、式 $(1)$ で成功と失敗のデータをどんどん掛け合わせていったことと同じことができそうです。

実際にやってみましょう。図6 をご覧ください。青い線が2021通年の日経平均の分布、グレーの線が2022年に入って新たに得た20日分の分布で、緑の線がこのふたつの正規分布を掛け合わせたものです。いずれも確率分布ですから面積は1で同じです。

図6

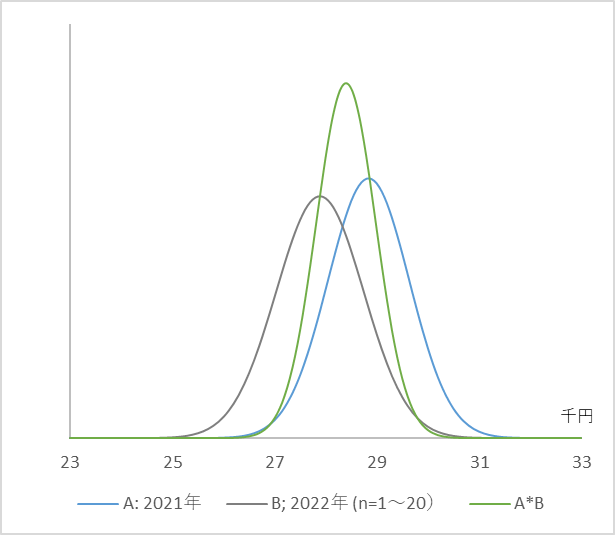
正規分布に正規分布を掛け合わせると正規分布になる!

 

掛け合わせた正規分布に、また次の20日間で得られる正規分布を掛け合わせる、という作業を四回繰り返して、直近のデータ（2022年1月4日から5月2日までの80個）まで反映させたら、図7の緑の曲線になります（註）。

図7

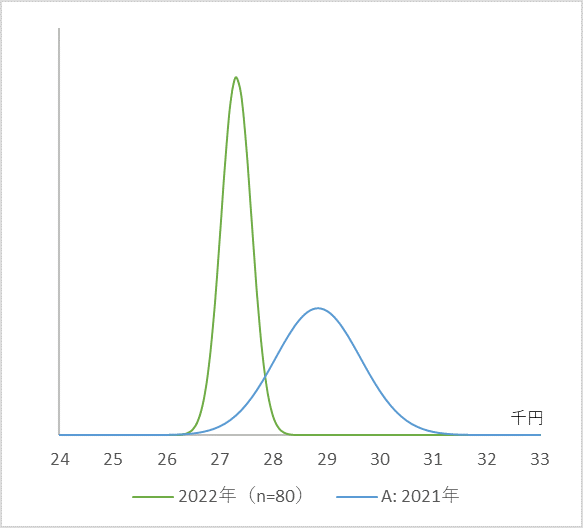
2021年の日経平均の出現確率分布を2022年の日経平均で20日ごとに四回更新したあとの同分布。

2021年：平均 28,800円、標準偏差 800円

2022年5月2日現在：平均 27,000円、標準偏差 460円

 

平均は昨年の2万9千円から2万7千円に下落、標準偏差は8百円から5百円弱となり、分布範囲が狭くなっています。つまり、今後の日経平均の出現幅はおよそ七割の確率で、「2万7千円 ± 5百円」と予測できます。

ついでながら、「正規分布の足し算」もみてみましょう。図8 は新型コロナ・ウィルスの週別死亡者数の推移を正規分布で近似したものです。死亡者数の山は、これまで大きく分けて六つあります。ピークに合わせて裾野の拡がり具合が実際のデータに合うようにフィッティングしていきます。三番目と四番目の裾野が重なりあっていますが、ふたつの正規分布を足し合わすだけでこうなります。また、直近の第六波ですが、第七波（オレンジの破線）が隠れていると捉えるとうまく近似できます。さらには、正規分布さえうまくフィッティングできれば、「釣鐘山の右下がりの裾野＝収束する時期」ですから、おおよその収束予測もできるというわけです。正規分布、とても便利ですね。

図8

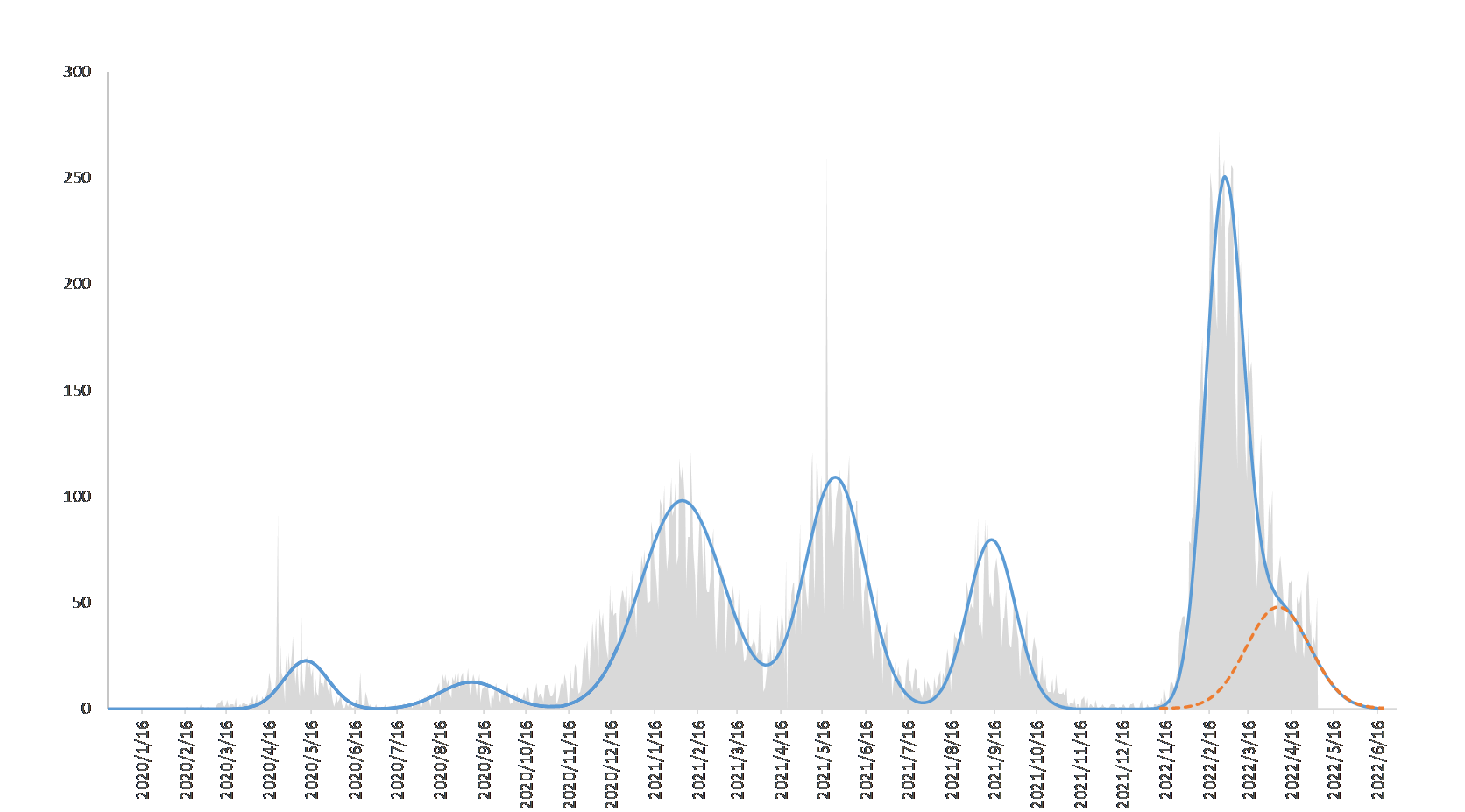
正規分布で近似した新型コロナ・ウィルスによる週別死亡者数の推移

正規分布を足し合わせるだけで近未来予測ができる事例

 

（註）正規分布の積を数式で表すと以下のとおりです。

$$f_{0}(x)=\frac{1}{\sqrt{2πσ_{0}^2}}exp(-\frac{(x-µ_{0})^2}{2σ_{0}^2})$$

$$f_{1}(x)=\frac{1}{\sqrt{2πσ_{1}^2}}exp(-\frac{(x-µ_{1})^2}{2σ_{1}^2})$$

$$f_{2}(x)=Cf_{0}(x)f_{1}(x)$$

$f_{0}(x)$ が事前のデータ、$f_{1}(x)$ が新たに得たデータ、そのふたつを掛け合わせてできる正規分布が $f_{2}(x)$ です。 $C$ は確率分布の面積を $1$ にするための規格化定数です。ちなみに、エクセル関数 =NORM.DIST(x,平均,標準偏差,FALSE) を使えば、数式を知らなくても簡単に正規分布のグラフを描くことができますし、$C$ もすぐに見つかります。

 

おわり

 

 

 

 

記事一覧へ戻る