2024年1月12日（金）、日経平均が三万五千円台に到達しました。巷では今年は1989年12月29日に記録した最高値（38,916円）を更新するのではないかと騒がれ始めています。図１が過去74年間の日経平均の推移です。1950年1月4日の終値 108.56 を 1.0 として、その成長倍率を示しています。過去最高値は358倍、本年1月12日の終値が328倍です。縦軸（成長倍率）は対数軸です。

図１

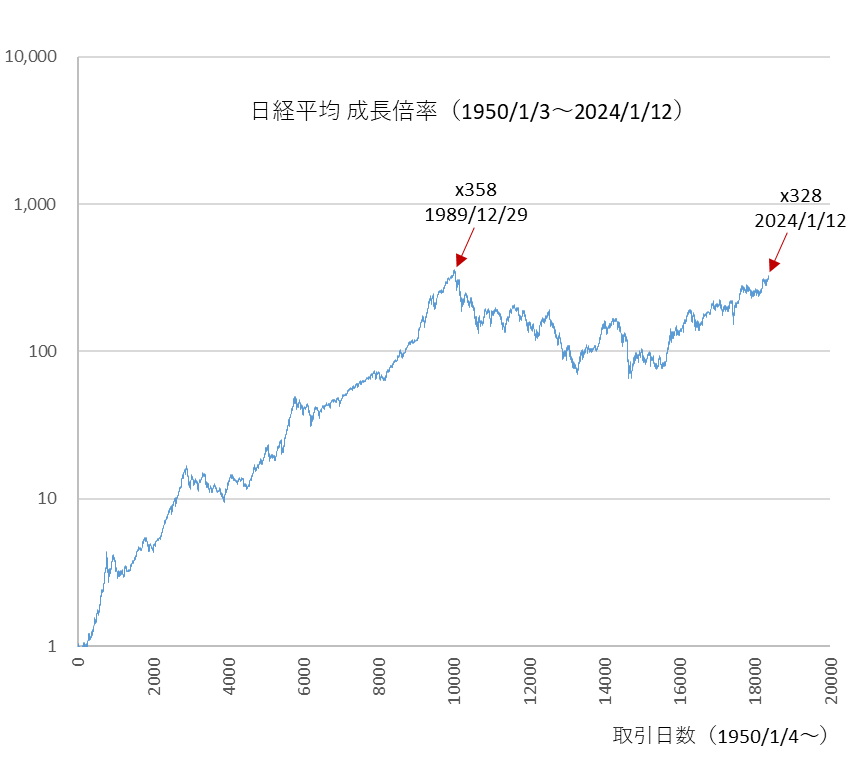
確かに1989年の最高値は35年経過した今日まで更新されていません。では図１に「三本の矢」を描き加えてみましょう。

１）現状維持を示す線（基準線）

２）平均的な成長を示す線（μ）

３）拡散範囲を示す線（±v）

スタート地点（初期値）を 1.0 とすれば上記のみっつはそれぞれ時間 $t$ の関数として、

$$x_{t}=1.0\tag{1}$$

$$x_{t}=x_{0}e^{(r-\frac{v^2}{2})t}\tag{2}$$

$$x_{t}=x_{0}e^{(r-\frac{v^2}{2})t+v\sqrt{t}}\tag{3}$$

で表すことができます。

 

図２

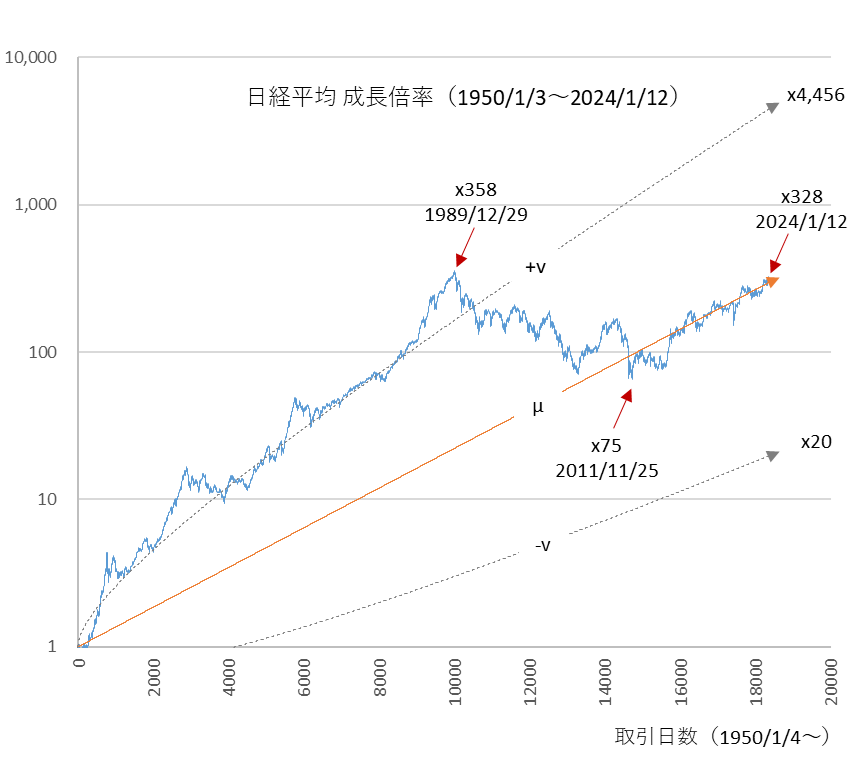
x₀=1.0, r=0.000516, v=0.02, r-v²/2=0.000316

中央線 $μ$ の終点が2024年1月12日の成長倍率に到達し、 $+v$ 線が実績におおよそ合致する $r$ と $v$ の組み合わせ

 

中央線の終点を 2024年1月12日の終値に合わせると、最高値以降の35年間（1989年～2024年）の内、約20年間（1989年～2011年）は調整期間という位置づけになります。では、中央線 $μ$ を前半の約40年間（1950年～1989年）に合わせて、後半の35年間（1989年～2024年）に $-v$ 線を合わせるとどうなるでしょうか。図３をご覧ください。

図３

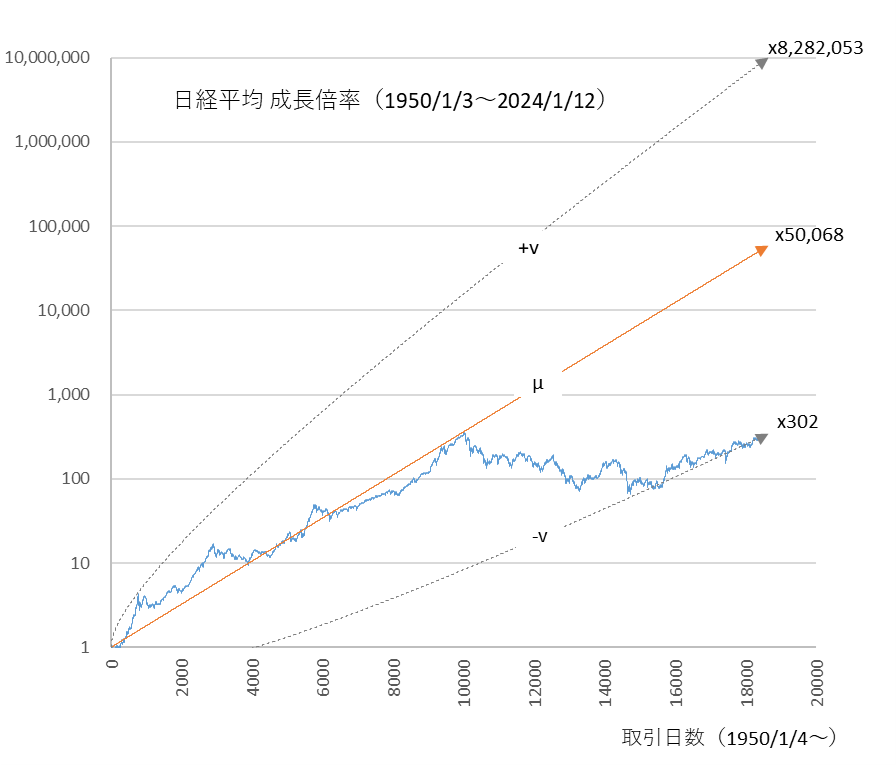
x₀=1.0, r=0.0013, v=0.0377, r-v²/2=0.000589

中央線 $μ$ が前半の40年間の成長に沿い、 $-v$ 線が実績におおよそ合致する $r$ と $v$ の組み合わせ

 

中央線 $μ$ が2024年1月12日に到達する成長倍率が 1950年1月4日の5万倍となります。ここで、同じ期間に米国の代表的な株価指数である S$P500 はどの推移していたのかを検証してみましょう。図４をご覧ください。

図４

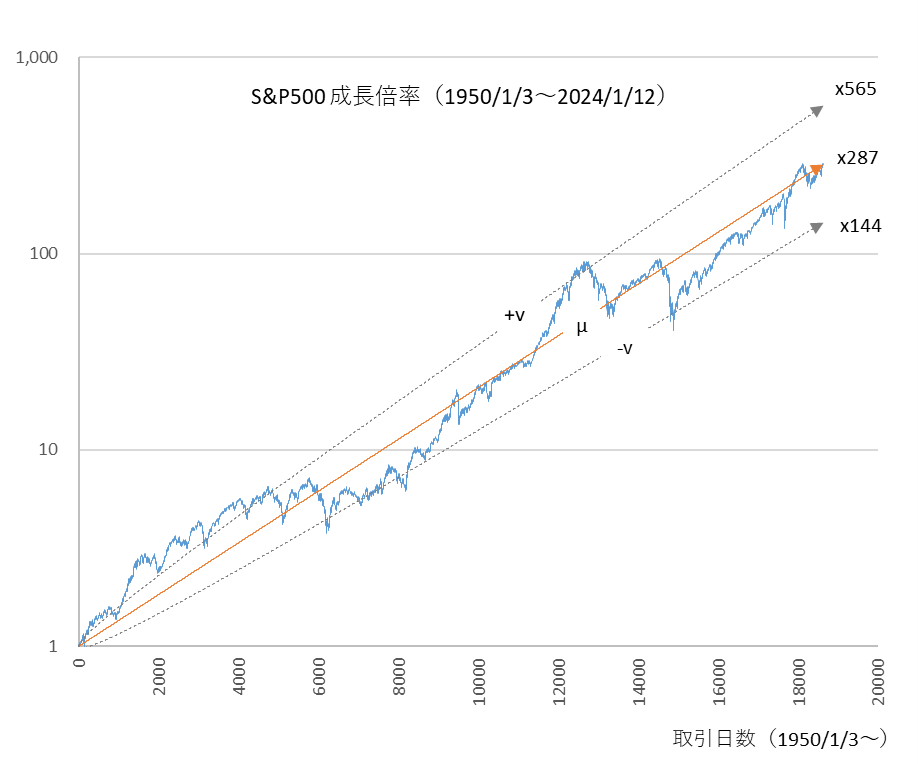
x₀=1.0, r=0.000316, v=0.005, r-v²/2=0.000304

中央線 $μ$ の終点が2024年1月12日の成長倍率に到達し、 $+v$ 線が実績におおよそ合致する $r$ と $v$ の組み合わせ

 

到達倍率が287倍です。世界経済はお互いにリンクしていることを考えると、日経平均だけが五万倍に成長することはあり得ません。やはり図１、つまり日本経済は失速したのではなく、前半の成長率が大きかっただけで後半にその調整が入ったとみるのが妥当です。S&P500の年間平均成長率（1950～2024年）は7.6%ですが、日経平均のそれは最高値の1989年までは27.1％と非常に高かったことがわかります。後半に調整が入って、74年間で均してみると7.7%ですから S&P500 とほぼ同じです。つまり、日経平均は、高成長→調整という期間を経て、ようやく巡航速度で成長しはじめたといえます。

ここで、「日経平均は今年4万円台に到達するか？」という冒頭の話に戻ります。もしこのまま巡航速度による成長が継続するとすれば、日経平均が4万円台に突入するのは $μ$ 線が368倍（40,000円÷108.56円）に到達する2026年の後半と予測できます（図５）。

図５

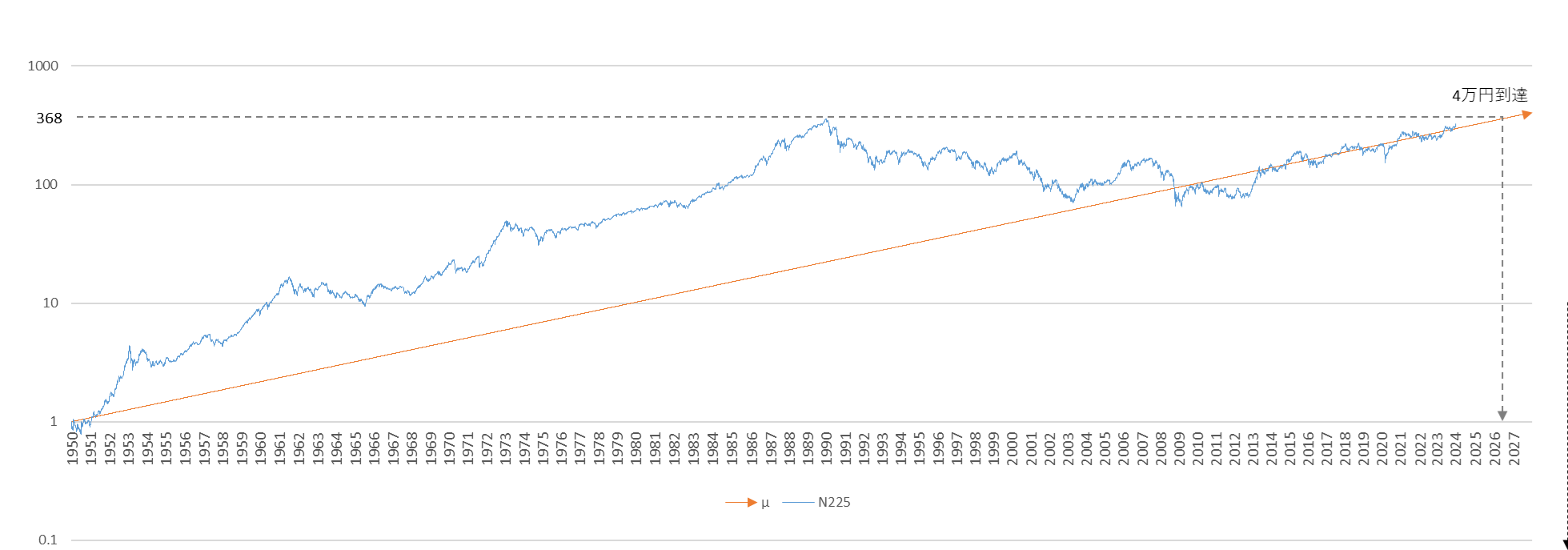
$μ$ 線が4万円（368倍成長）に到達するのは2026年の後半

 

 

つづく

記事一覧へ戻る