2023年1月8付のブログで、世界の株価指数の二年間の分布推移が拡散移流方程式によってうまく近似できることをつきとめましたが、今回は別のアプローチを試みます。では、解析するデータを再度掲載します。
図1
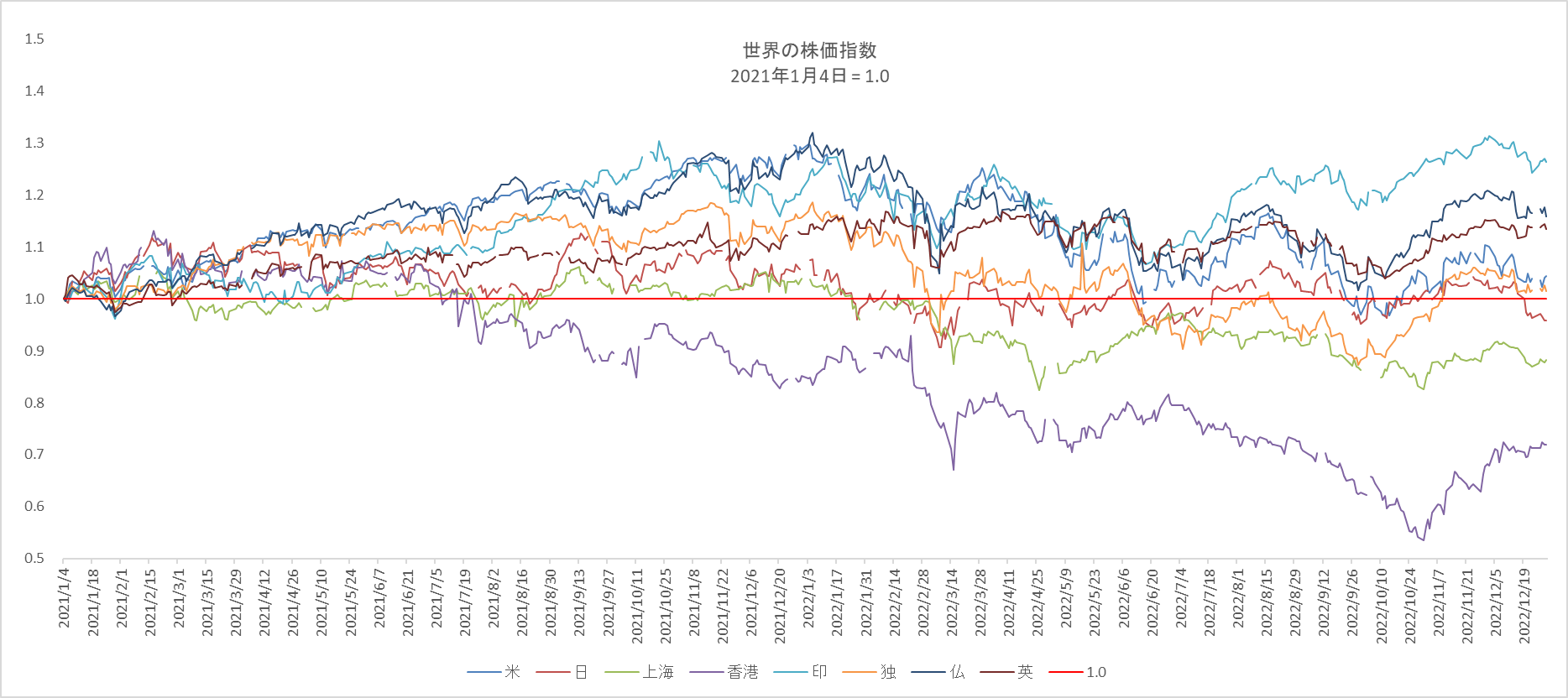
世界の代表的な株価指数の初期値を 1.0 に合わせてその後の推移をグラフ化したもの。
川へ落としたインクが拡散しながら流れていく様子に似ている。
前回の議論は上下のばらつき(拡散)と右方向への移動(移流)に注目したわけですが、今回は個別の株価が描くぎざぎざな動きをみます。株価は単純に初期値と日々の変化率によって決まりますから、初期値を $x_{0}$ として日々の変化率を $v_{1}$、$v_{2}$、$v_{3}$・・・とすると、
$$x_{1}=x_{0}(1+v_{1})$$
$$x_{2}=x_{1}(1+v_{2})=x_{0}(1+v_{1})(1+v_{2})$$
$$x_{3}=x_{2}(1+v_{3})=x_{0}(1+v_{1})(1+v_{2})(1+v_{3})$$
・
・
$$x_{n}=x_{n-1}(1+v_{n})=x_{0}(1+v_{1})(1+v_{2})(1+v_{3})・・・(1+v_{n})\tag{1}$$
となります。表1は八か国のインデックスの変化率 $v_{n}$ の二年間の実績をまとめたものです。
表1
2021~2022年の変化率 |
米 S&P500 | 日 N225 | 上海 SSE | 香港 HSI | 印 BSE | 独 GDAX | 仏 CAC40 | 英 FTSE |
| 総数 | 503 | 487 | 486 | 493 | 496 | 510 | 512 | 493 |
| プラス成長 | 253 | 250 | 242 | 239 | 254 | 270 | 279 | 265 |
| マイナス成長 | 250 | 237 | 244 | 254 | 242 | 240 | 233 | 228 |
| プラス平均 | 0.935% | 0.961% | 0.776% | 1.304% | 0.859% | 0.879% | 0.828% | 0.679% |
| マイナス平均 | -0.914% | -1.015% | -0.808% | -1.322% | -0.793% | -0.964% | -0.912% | -0.754% |
| 全平均 | 0.016% | -0.001% | -0.020% | -0.049% | 0.053% | 0.012% | 0.036% | 0.030% |
| 標準偏差 | 1.239% | 1.284% | 1.112% | 1.880% | 1.115% | 1.355% | 1.222% | 0.996% |
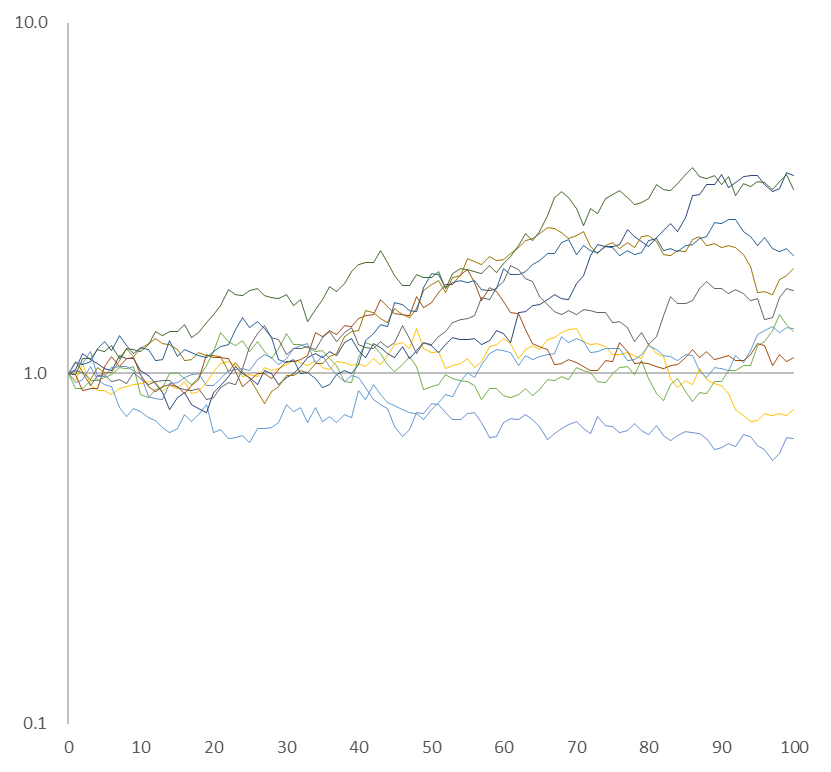
たとえば米国の S&P500 ですと、2021~2022年の二年間に変化率が 503回発生(取引日数は504日)していて、その内プラス成長が253回、マイナス成長が250回でした。そして、プラスの成長率の平均が 0.935%、マイナスが 0.914% です。すべての変化率の平均は0.016%、標準偏差が1.239%です。
上海と香港は上昇した回数よりも下降した回数の方が多くなっており、変化率全体の平均もマイナスでした。
ここで、変化率の平均と標準偏差に注目して図示すると、
図2
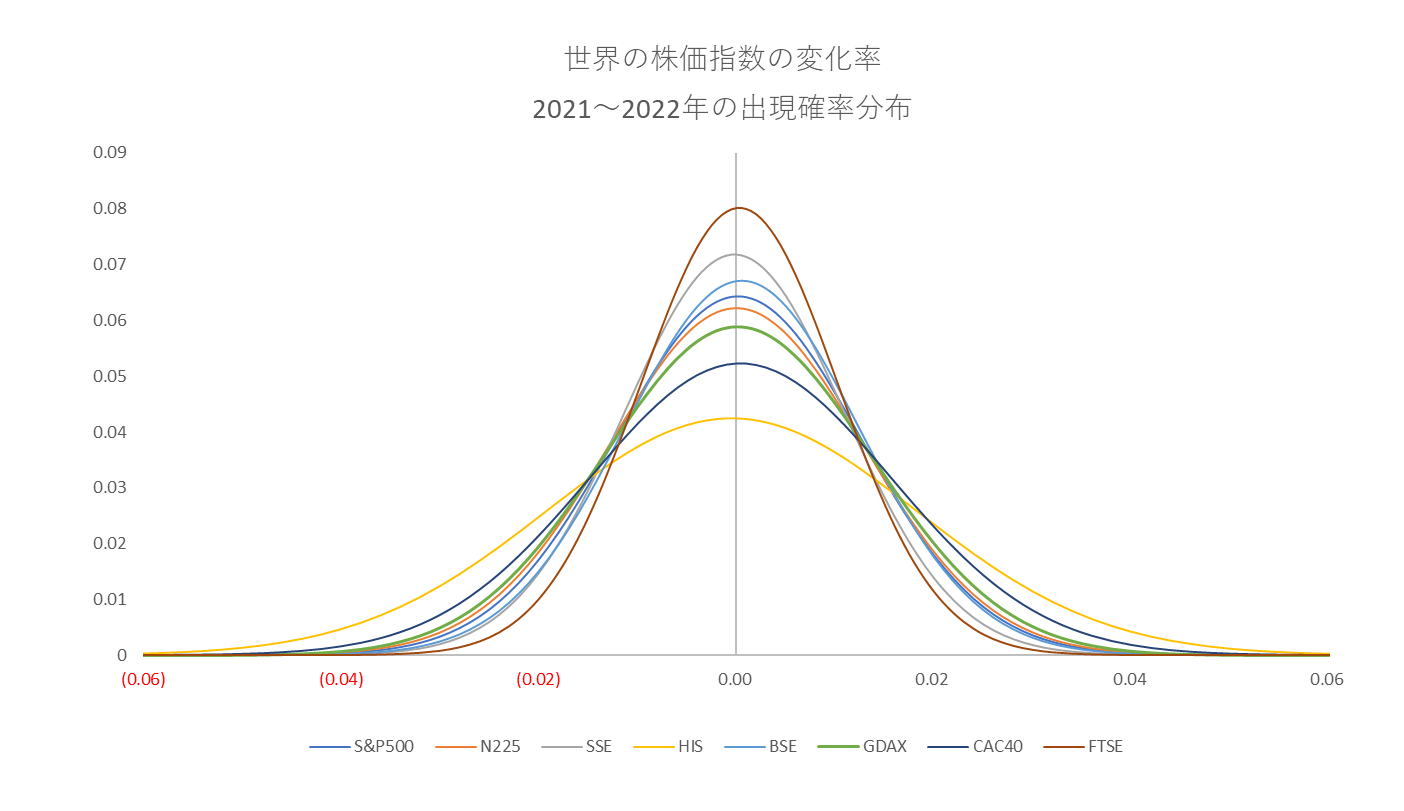
世界の株価指数の変化率分布(表1の平均と標準偏差で描いた正規分布曲線)
横軸が変化率、縦軸がその出現確率(各ベルカーブに囲まれた面積は $1.0$ )
となり、二年後の値下率が最も大きかった香港の分布にばらつきが多いことがわかります。図1の赤線に注目してください。これより上がプラス成長、下がマイナス成長です。二年後にマイナス成長であったのは八か所の内、日本、上海、香港の三か所で、残りの五か所はプラス成長でした。そこで標準偏差が大きい、つまり「変化率のばらつきが大きければ大きいほど成長が鈍化する」という仮説を立ててみましょう。
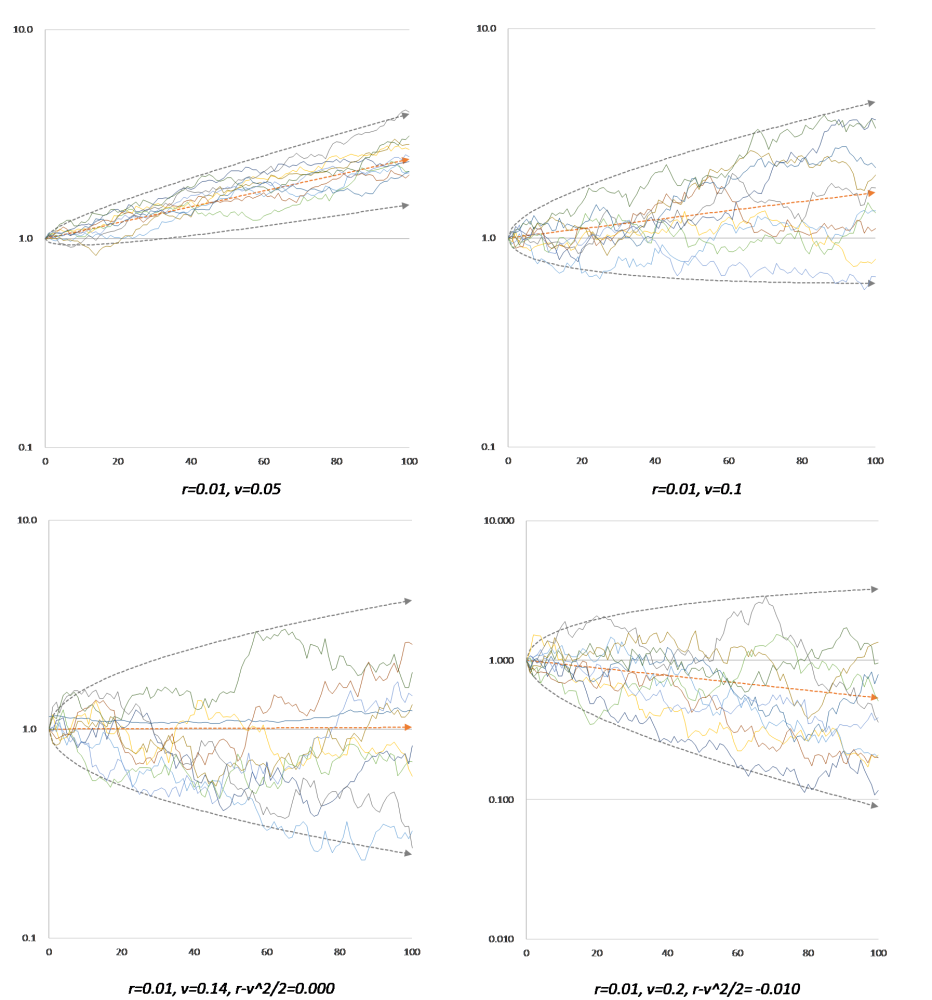
図3-1~図3-3は表1のそれぞれの平均はそのままにして、標準偏差だけを変化させたとき、二年後の終値がどう変化するかをシミュレートした結果です。
図3
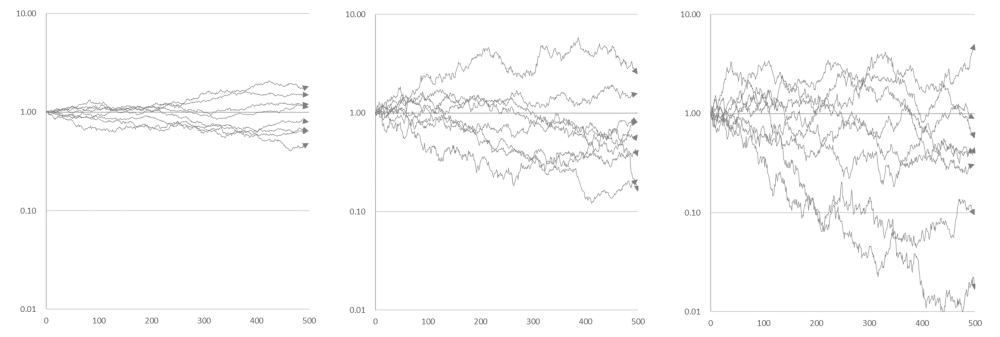
標準偏差の倍数:左から、一倍、三倍、五倍 (縦軸は対数)
標準偏差が大きくなればなるほどばらつきが大きくなりマイナス成長する確率が高くなる。
確かに、標準偏差が大きくなればなるほどマイナス成長する数が増えています。図4は標準偏差を変えながらそれぞれ100回試行したとき、プラス成長できた数を集計したものです。
図4
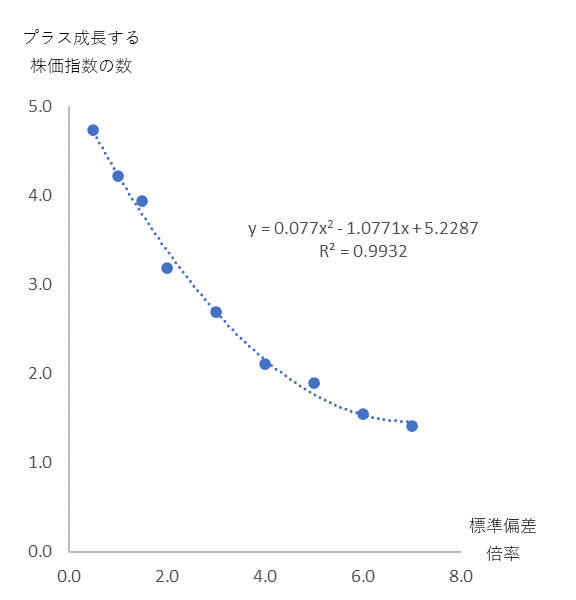
変化率の標準偏差を変化させて、それぞれ100回試行したときに二年後にプラス成長した株価指数の数。
標準偏差が大きくなればなるほど成長が鈍化するのが分かる。
実験の結果、確かに変化率のばらつきが大きいと成長が鈍化することがわかりましたが、これを数学的にどのように証明すればいいでしょうか。
株価の変化率は以下の確率微分方程式で表現できるとされています。
$$\frac{dx}{dt}=rx+vx\frac{dB}{dt}\tag{2}$$
$r$ は成長係数、$v$ はゆらぎ係数、$B$ はブラウン運動(微細なランダム運動)です。
式 $(2)$ の解は、$x_{0}$ を初期値とするとき、
$$x_{t}=x_{0}\ e^{(r-\frac{v^2}{2})t+vB}\tag{3}$$
であることがわかっています。
式 $(3)$ は、
$$x_{t}=x_{0}\ e^{(r-\frac{v^2}{2})t}e^{vB}\tag{4}$$
と分解できます。$r-\frac{v^2}{2}$ は定数ですから、$x$ は、
① 一定の割合で指数増加 $e^{(r-\frac{v^2}{2})t}$ しながら、
② ブラウン運動 $e^{vB}$ する、
つまり、図5のような組み合わせになっているはずです。
図5
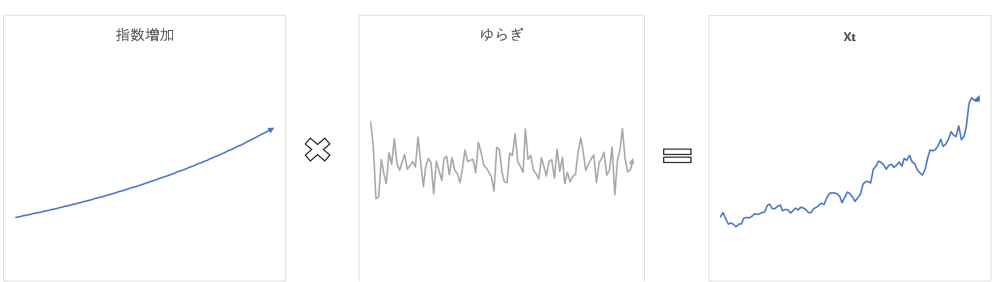
株価が確率微分方程式 式 (2) に基づき変化すると仮定すると、その解は一定の「指数増加」と「ゆらぎ」が組み合わさった動きをする。
図6は式 $(3)$ に $r=0.01$ 、$v=0.1$ 、$B=$ 平均 $0$、標準偏差 $1$ のランダムな値として、10回試行したときの $x$ の動きです。
図6
x0=1、r=0.01、v=0.1、B=NORMINV(RAND(),0,1)、t=1~100、試行回数=10回
プラス成長が八本、マイナス成長が二本
注)=NORMINV(RAND(),0,1) は平均 0、標準偏差 1 となる値をランダムに返すエクセル関数
ここで、式 $(4)$ をもう一度よく観察してみましょう。
$$x_{t}=x_{0}\ e^{(r-\frac{v^2}{2})t}e^{vB}\tag{4}$$
$e$ の右肩に乗っている指数 $r-\frac{v^2}{2}$ に注目すると、
$r>\frac{v^2}{2}$ → 指数がプラス → $x$ はプラス成長
$r<\frac{v^2}{2}$ → 指数がマイナス → $x$ はマイナス成長
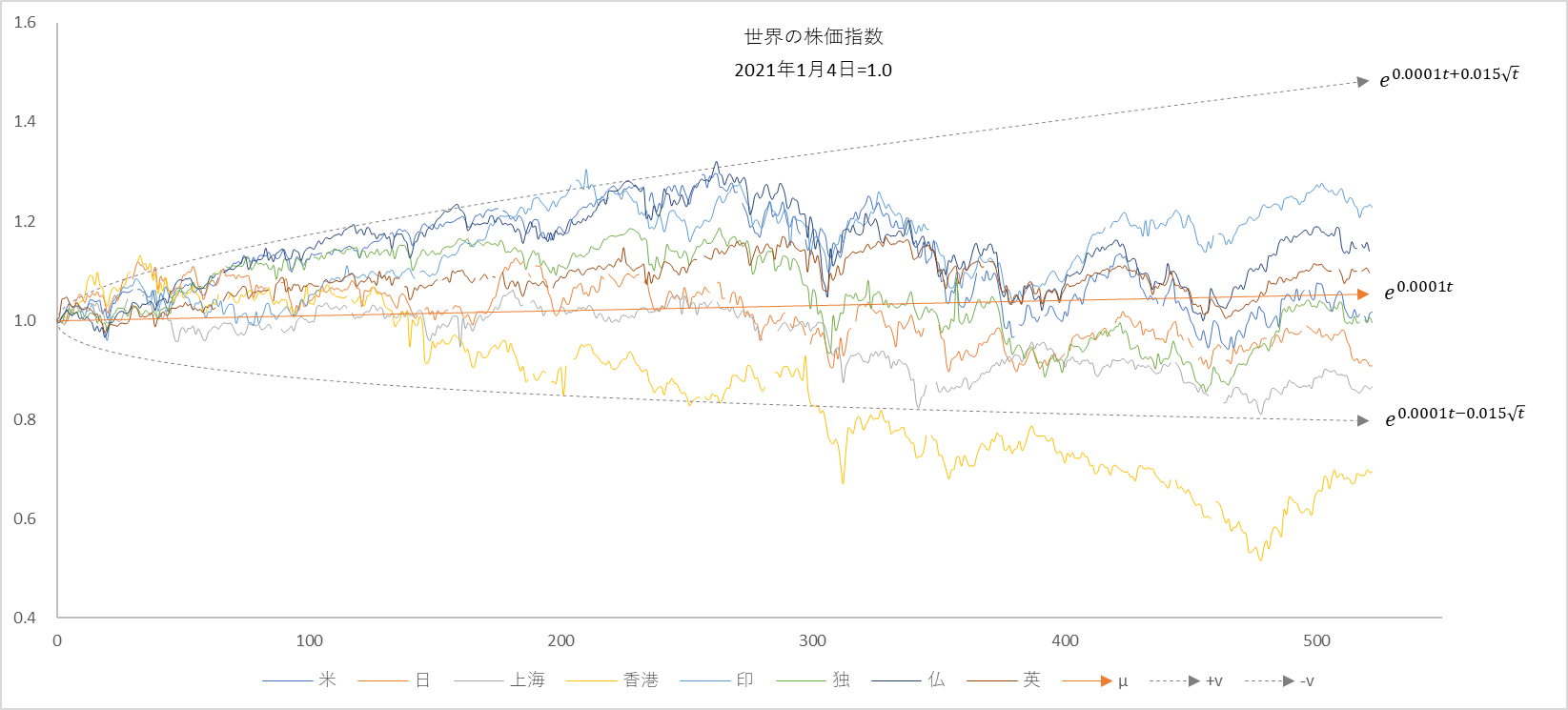
となることがわかります。つまり、成長係数 $r$ とゆらぎ係数 $v$ の組み合わせによって、$x$ が辿る運命は大きな影響を受けるといえます。図7は $r$ を固定して $v$ の値を変えたときの $x$ の様子です。オレンジの破線がゆらぎがないときの指数関数増加 $e^{(r-\frac{v^2}{2})t}$ を、グレーの破線がブラウン運動 $e^{vB}$ によってゆらぐ範囲 $e^{(r-\frac{v^2}{2})t+\sqrt{t}}$ を示しています。
図7
確かに、$v$ の値が大きくなればなるほど成長が鈍化しています。では、図1にもオレンジとグレーの破線をかぶせてみましょう。
図8
世界の代表的な株価指数の二年間(2021~2022)の推移
オレンジの破線がゆらぎのない指数関数増加 $e^{(r-\frac{v^2}{2})t}$ 、
グレーの破線がブラウン運動 $e^{vB}$ によってゆらぐ範囲 $e^{(r-\frac{v^2}{2})t+\sqrt{t}} $
r=0.0001, v=0.015
金融工学では株価のゆらぎ度合いのことをボラティリティ(volatility)と呼ばれています。volatilility とは「変わりやすい」という意味の volatile の名詞です。ゆらぎ係数の $v$ は volatility の頭文字です。 投資家心理においては、$v$ の大きさは値下がりリスクよりも値上がりへの期待感につながりがちです。また下落してもそのうち回復するだろうと期待してしまうのも投資家心理ですが、図8をじっくり観察すると、「一旦下降モードに入るとなかなか上昇モードにならない」こともわかります。香港や上海がそうであるように。
こうなると、式 $(3)$ の指数 $r-\frac{v^2}{2}$ が非常に大きな意味をもっていることに注目せざるを得ません。確率微分方程式
$$\frac{dx}{dt}=rx+vx\frac{dB}{dt}\tag{2}$$
の解はなぜ、
$$x_{t}=x_{0}\ e^{(r-\frac{v^2}{2})t+vB}\tag{3}$$
なんでしょうか。そして、 $r-\frac{v^2}{2}$ は一体どこから現われたのでしょうか?
おわり
記事一覧へ戻る