N字成長 – Excel日々、ランダムに上がったり下がったりを繰り返す株価ですが、それをチャートにしたときにある特長があることをご紹介します。

株価は前日に比べ0.5%上がった、0.3%下がった、というようなことを日々繰り返します。ここで重要なのは、上がった下がったといっているのが株価額ではなく変化率であるという点です。ある量の変化率がその量の現在値に比例するというような状況において生じるのが指数関数で、そのような現象のことを指数関数的増加または減少といいます。まさに株価はそれに当てはまります。

指数関数的増加をしようとしている中で絶えず上下にゆらぐのが株価です。これがシンプルな前提条件です。そして、それを数式で表現すると以下のようになります。

$$\begin{array}{}\text{(1)}& \frac{dx}{dt}=rx+vx\frac{dB(t)}{dt}\end{array}$$

 $x$ は株価、 $r$ は成長係数、$v$ はゆらぎ係数、$B(t)$ はランダムな動き（ブラウン運動）です。経営者が日々の判断を積み重ねることで会社が成長するのと同じで、株価も日々の変化率の積み重ねによって成長します。式 $(1)$ が日々繰り返されることによってチャートが形成されるのです。数学的には式 $(1)$ を微分方程式といい、それを積み重ねることを積分といいます。具体的な積分の仕方は専門書にゆずりここでは結果だけを示します。

$$\begin{array}{}\text{(2)}& x=x_0{e}^{(r-\frac{v^2}{2})+vB(t)}\end{array}$$

式 $(2)$ によって、任意の初期値 $x_0$から時間 $t$ が経過したときの株価を求めることができます。ここで、もしブラウン項の $vB(t)$ がなければ式 $(3)$ となります。株価 $x$ が向かう基本的方向を示しており、実際の株価 $x$ はこの式 $(3)$ を中心として上下にゆらぎます。以下、この中心線のことを $\mu$ 線と呼びます。

$$\begin{array}{}\text{(3)}& x=x_0{e}^{(r-\frac{v^2}{2})}\end{array}$$

$\mu$ 線からのゆらぎの度合いは式 $(4)$ で表せます。□が $\pm 1$の場合の指数曲線を$\pm 1v$、$\pm 2$の場合を $\pm 2v$ とし、総称して $v$ 線と呼ぶことにします。

$$\begin{array}{}\text{(4)}& x=x_0{e}^{(r-\frac{v^2}{2}+v\square \sqrt{t})}\end{array}$$

では、実際の株価がこの理論通りに動いているかどうかをみてみましょう。図1は前述したS&P500の2016年1月以降の動きです。縦軸が対数であることに注意してください。縦軸を対数にすると指数関数増加である中心線 $\mu$ は直線になります。マイナスの $v$ 曲線は短期的には一旦下降しますが、長期的にはプラスに転じます。よって、$\mu$ 線と $v$ 線の全体の形は右肩上がりのハレー彗星のようになります。そして株価はこのハレー彗星の中で行ったり来たりを繰り返します。

図1

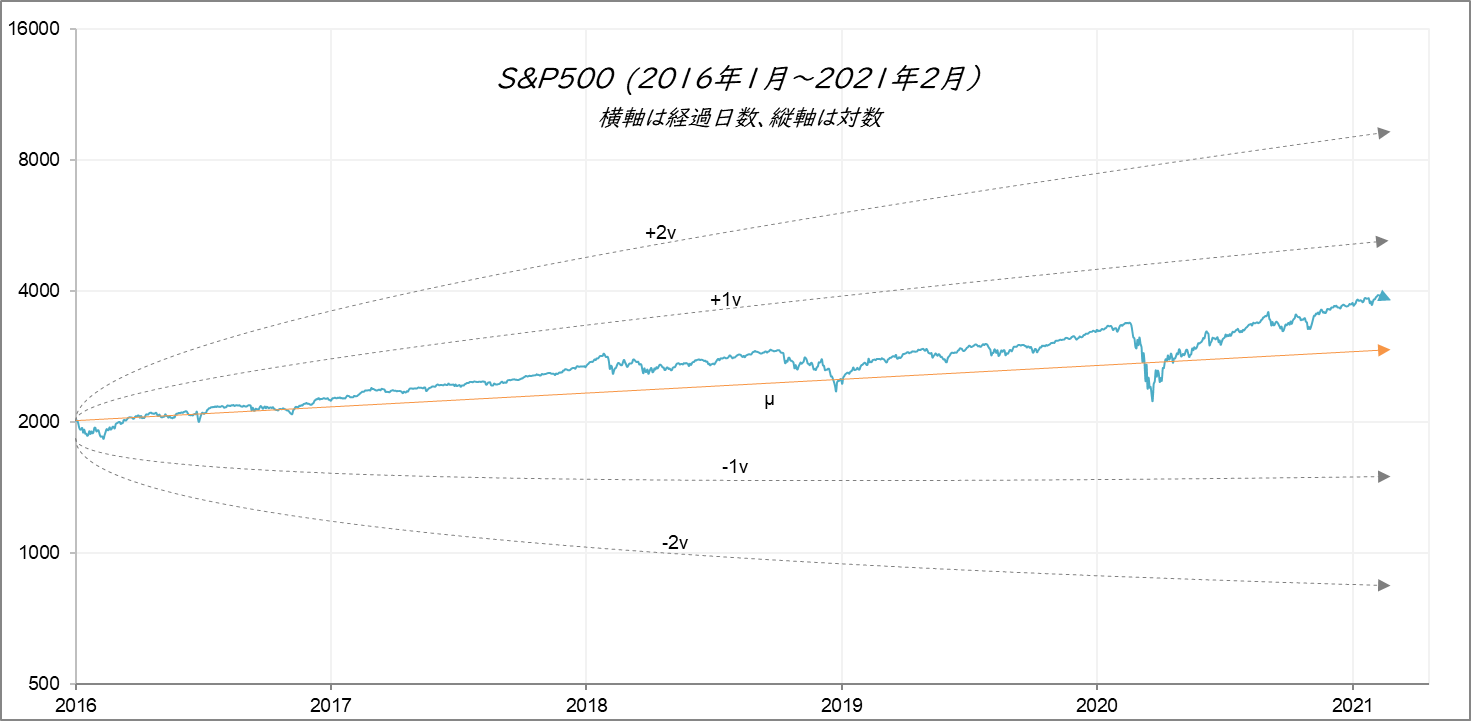
2016年1月を起点とするµ線とv線。確率微分方程式の解から算出。$x_0=2012.66,r=0.00042,v=0.016$

係数の決め方は2020年4月21日付のブログ「コロナショックによる株価下落の回復はいつか 」を参照してください。

 

ここで、図1を少しズームアップして株価の動きに注目するといくつかの転換点があることに気が付きます。たとえば、図2の丸印で示した点です。

図2

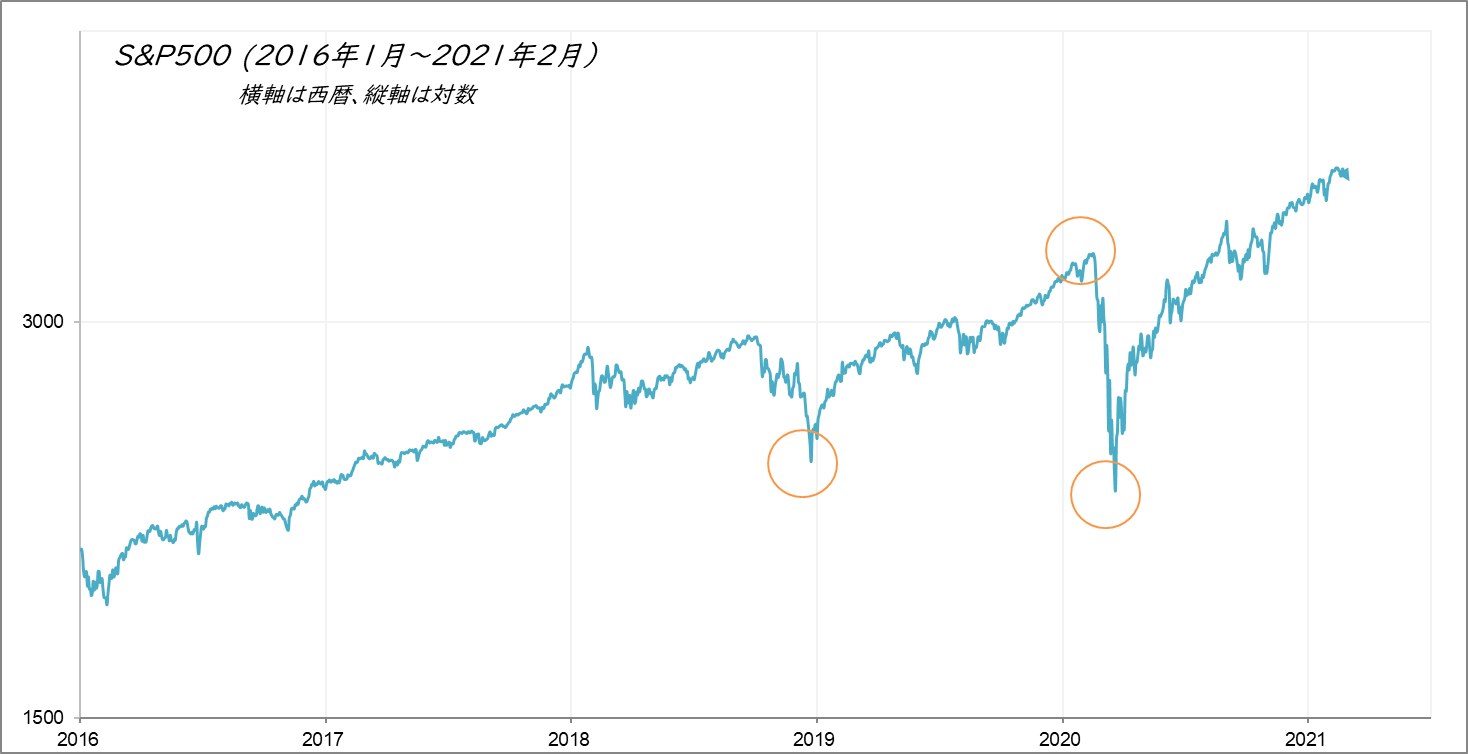
S&P500の大きな転換点である頂（ピーク）と谷（バレー）。

 

式 $(3)$ と式 $(4)$ の初期値にこれらの転換点を代入してそれぞれの $\mu$ 線と $v$ 線を書き込んだものが図3です。

図3

ピーク＆バレーを起点するv曲線

$x_0=2930.75,2351.10,2237.40,r=0.00042,v=0.016$

 

過去5年間でみると株価は $\mu$ 線と $+1v$ 線の間を動いていましたが、もう少し短期的に観察すると、 $+1v$、$-2v$（未満）、$+2v$ 線上というように、それぞれ上昇と下降の度合いに違いがあることが分ります。起点をさらに二か所増やして、$v$の値を実際の株価に合うように調整したものが図4です。

図4

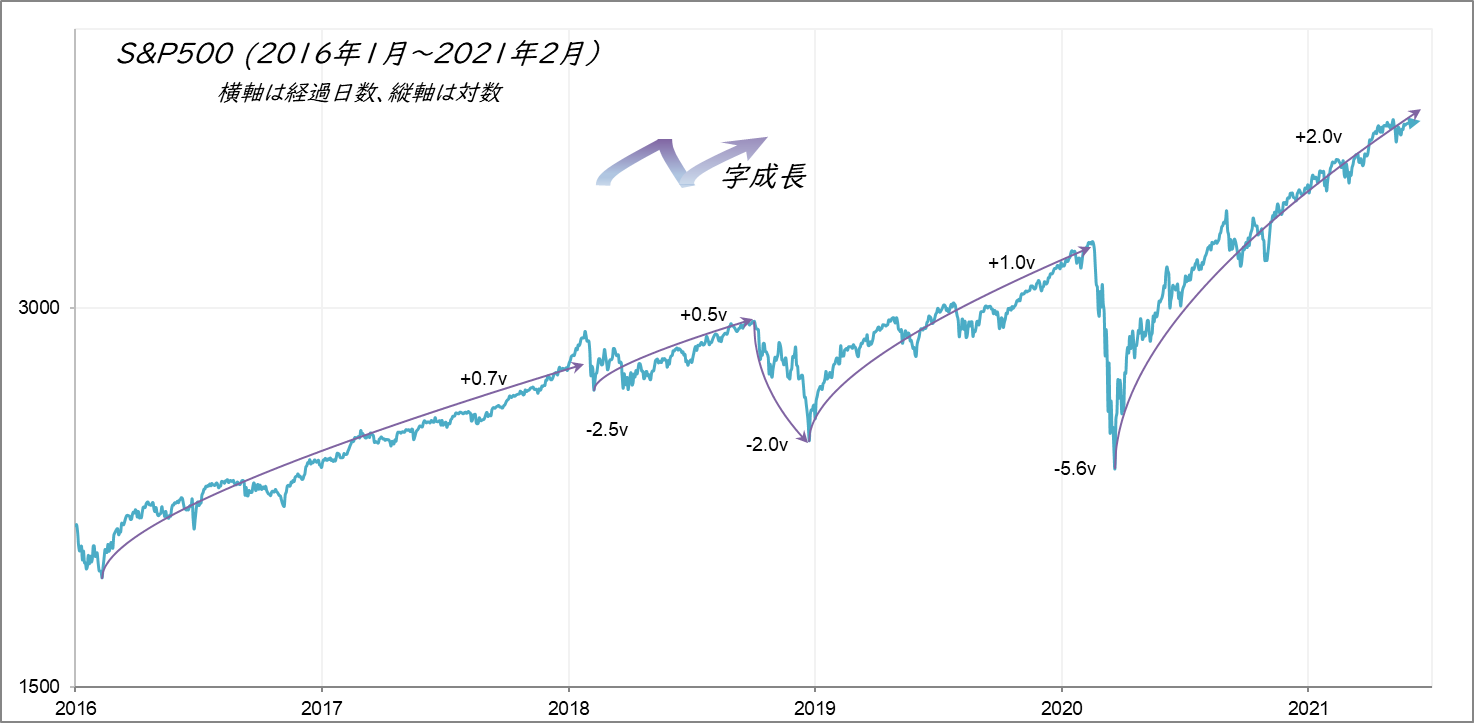
ピーク＆バレーを起点とするv線

$x_0=2012.66,2581.88,2930.75,2351.10,3386.10,2237.40,r=0.00042,v=0.016$

 

図4は株価が 「上に凸の曲線 → 下に凸の曲線 → 上に凸の曲線」に沿うという特長があることを明確に示しています。つまり、N 字が次々と現れます。

つづく

 

<修正・追記＞

2021年6月20日に、図3と図4を一部修正しました。

2021年6月20日に、計算の詳細 N字成長 – Excel を追加しました。

 

記事一覧へ戻る