2020年4月16日付のブログ「外出自粛は新型コロナ・ウィルス感染症の収束を速めるか？」においてひととひとの接触を減らすことがもっとも即効性のある方法であることを簡単な微分方程式から導きました。では、その後、実際の感染者数は予測どおりに推移したでしょうか？

緊急事態宣言の発出もあり感染者数（週単位、以後同様）は五月末に一旦収束に向かいましたが、六月末ごろからまた増加しはじめ、八月の中頃には一万人に達しました。その後、減少に転じるも四千人を切ったあたりで停滞し始め、十月以降はまた増加に転じています。図１は厚生労働省が公表している感染者数を週別に集計したものです。

図１

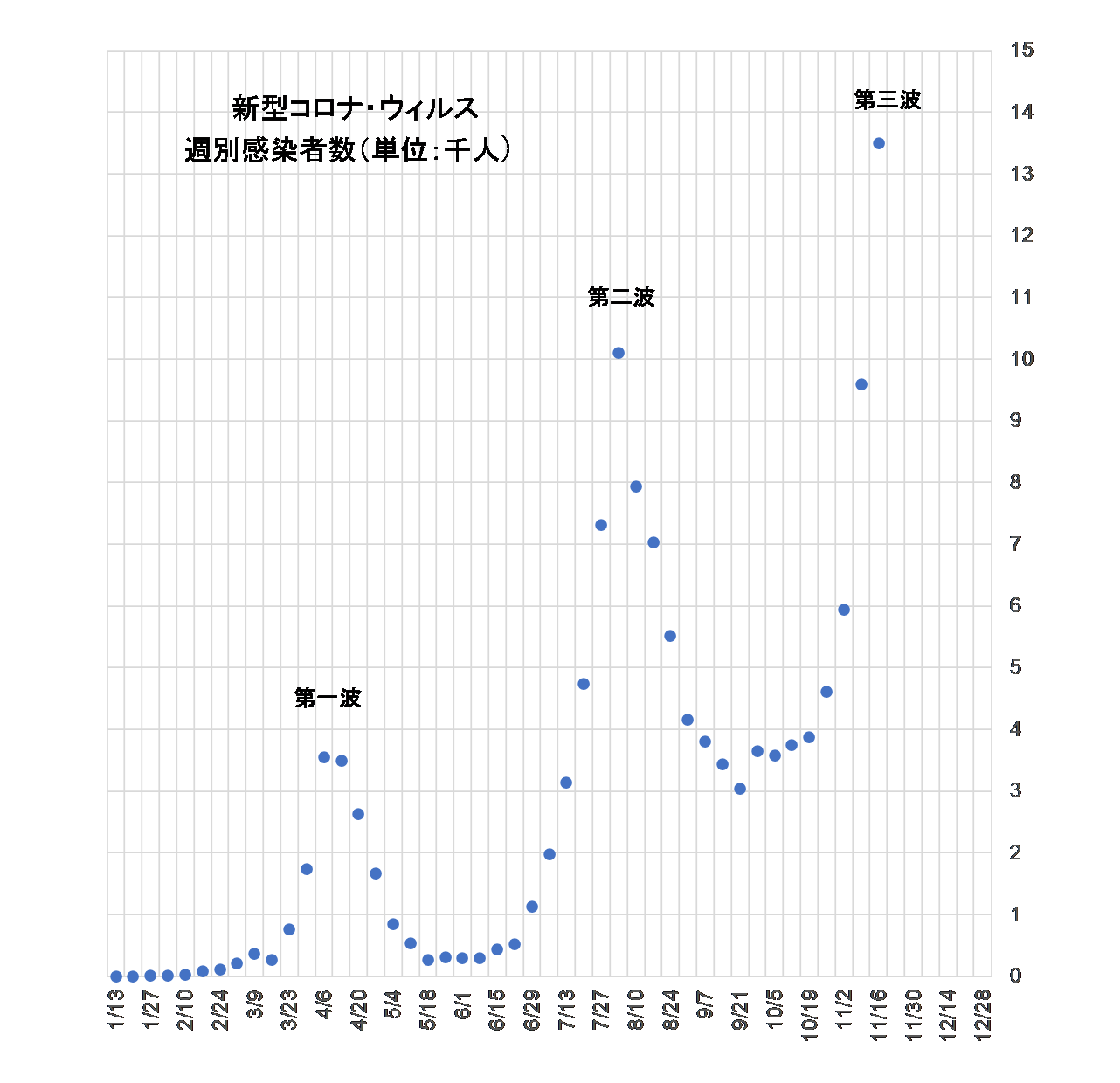
この波打ち現象は当初予測をしていませんでした。なぜならば、以下に述べる理由により感染する可能性があるひとが一定の数を下回ると感染が止まるからです。

ひとは単純に新型コロナ・ウィルスの感染者と未感染者に二分されます。

感染者数はウィルスの感染力によって増えますが、感染したら免疫または死亡によって感染する可能性がなくなります。

感染力を表す係数 を $b$、治癒するか死亡するかの度合いを表す係数を $c$ とすれば①と②は次の微分方程式によって定義されます。

感染する可能性のあるひと $x$ の変化率 :

$$\frac{dx}{dt} = -bxy \tag{1}$$　

式 $(1)$ は感染者 $y$ と接触して感染することで $x$ が減少することを示しています。$x$ はあくまで「感染する可能性のあるひと」ですので、たとえば外出しないひととか、感染対策を施しているひと、または施された環境にいるひとなどは除外されます。

感染者の数  $y$ の変化率　：　

$$\frac{dy}{dt} = bxy – cy \tag{2}$$

式 $(2)$ は $x$ との接触によって 感染者 $y$  が増える一方で、治癒や死亡によって減少することを示しています。ここで、

$$bxy – cy = 0$$

とおくと、

$$x = \frac{c}{b}$$

ですから、$x$ が $\frac{c}{b}$ に達すると 感染者数 $y$ は減少に転じます。

ところが、実際には図1のとおり、一旦、減少に転じてもまた増加するという現象がすでに二度起こっています。感染すると抗体ができて二度と同じウィルスには感染しないとすれば、第二波や第三波はウィルス自体の変異によるものであると考えるのが自然です。

ただ、ここでもうひとつ不思議な現象がみられます。第三波は第二波が収束しないうちにはじまっていることです。なにか原因があるはずです。そこで、第二波と第三波の間にもうひとつ別の変異ウィルスが隠れているのではないかという仮説を立ててみます。第二・五波があったとすれば、感染者数はこれら三つの波を合成したものになります。その「合成波」を図２の破線で示しました。

図２

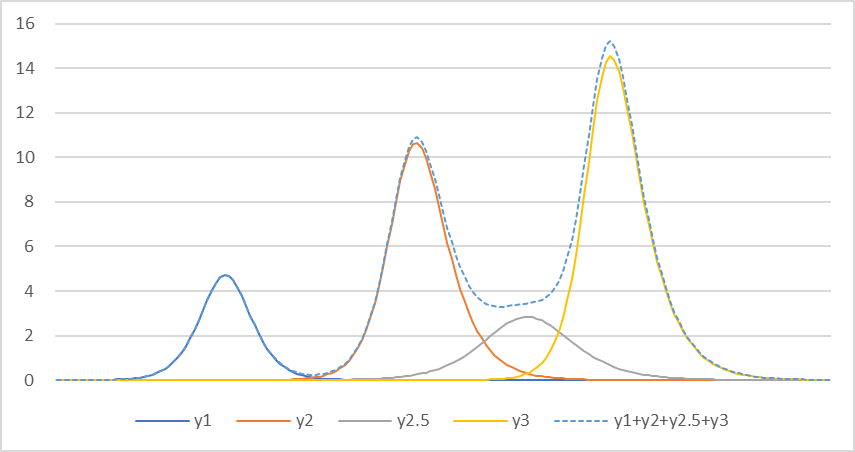
第二・五波の発生時期や感染係数 $b$、治死係数 $c$ を適宜変化させ、実際のデータに合成波（破線）をフィッティングをした結果が図３です。

図３

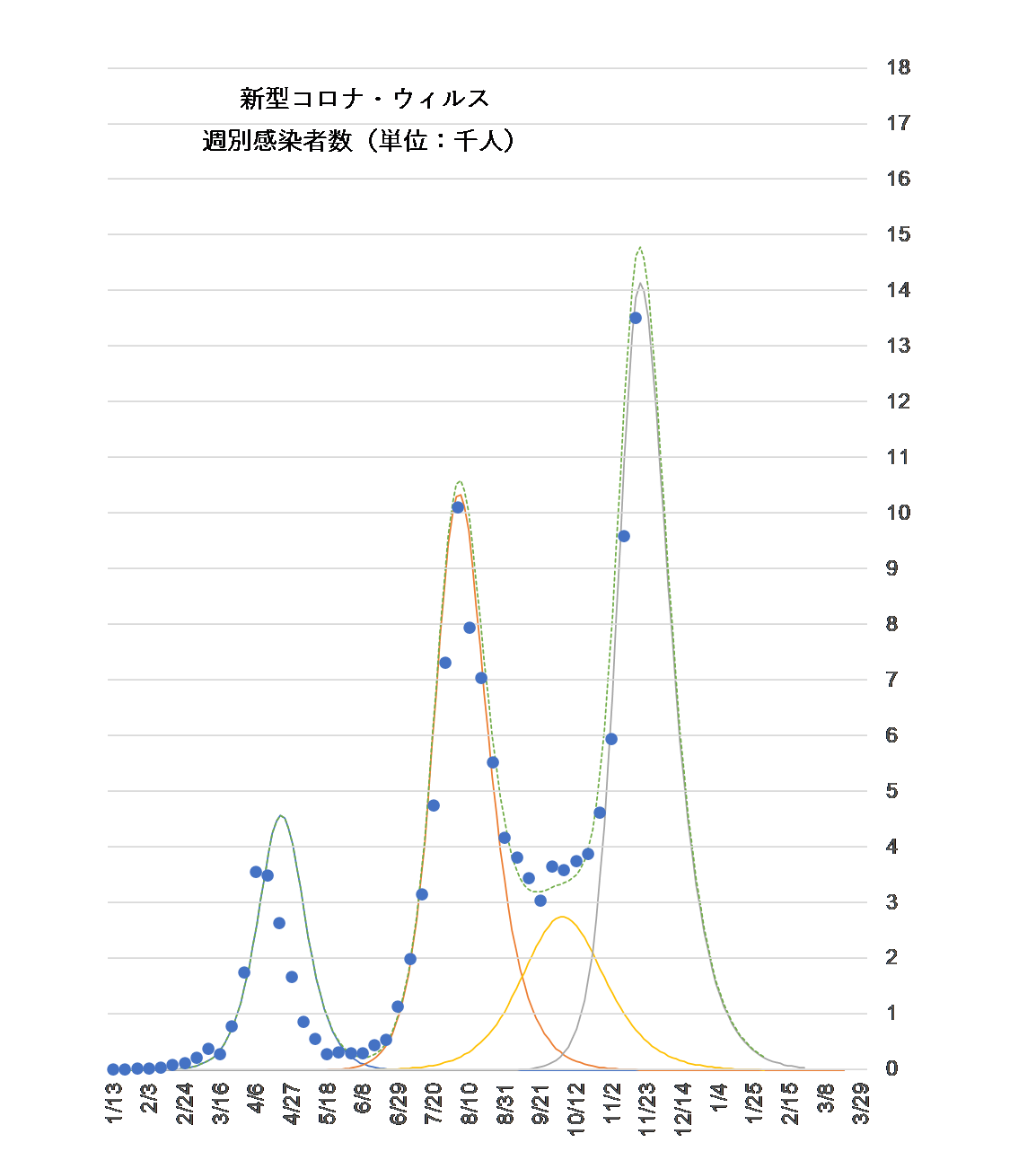
第二・五波（黄色の実線）の存在をあぶり出すことによって、理論値の合成波が実際のデータとうまく合致します。

今後も変異種が出現し続ける可能性を否定することはできませんが、少なくとも、第三波（種）単独の推移については、ピークが11月末、収束は来年の2月ごろである、と予測できます。

感染拡大防止策は広範囲な産業に対して経済的なダメージを与えることが明らかとなり、「接触を減らす」という対策には限界があることも分かりました。安全且つ有効な抗ウィルス剤やワクチンの早期製品化・投与が待たれますが、ウィルスが絶えず変異するのであれば、投薬の効果も限定的になる可能性があります。数理論は感染症が遅かれ早かれ必ず収束することを示しており、実際のデータもそのとおりに推移しています。不必要な恐怖心に煽られることなく冷静に対処していきたいところです。

以上

 

＜2021年8月18日追記＞

変異種が連続して出現する理由については、2021年8月18日付ブログ「新型コロナウィルス変異種の存在を説明する数理モデル」も参照ください。

記事一覧へ戻る