2025年1月6日付のブログで以下の微分方程式が複数の株価の動きを表現できることを具体例で示しました。
右辺の第一項が拡散、第二項が移流です。$D$ と $C$ はそれぞれの速度係数です。
図1は個別銘柄(ブリヂストン、資生堂、三菱UFJ、トヨタ自動車、ソフトバンク)と TOPIX の動きです。2021年初から2024年末までの日次終値の推移です。2021年1月4日の各社及びトピックスの終値を1.0に揃えました。
図1
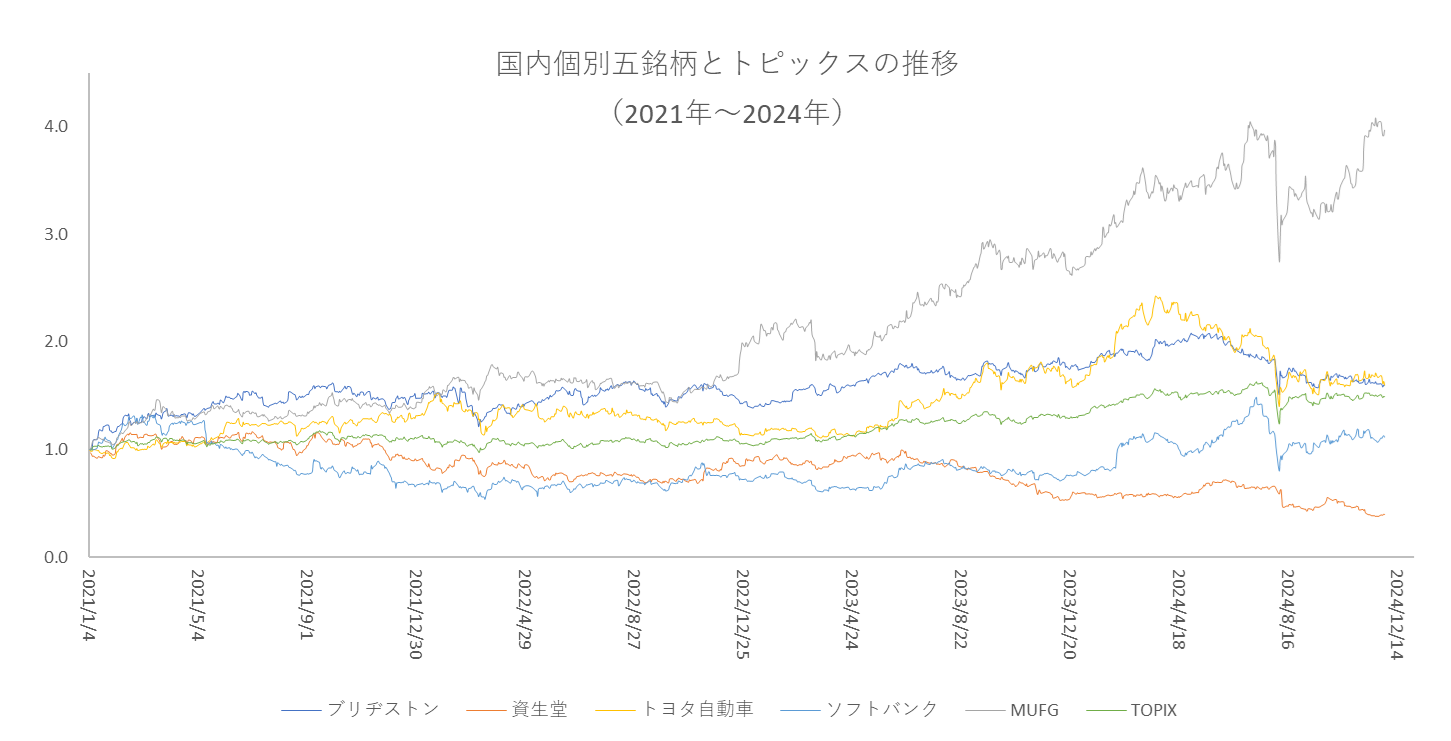
2021年~2024年の国内個別銘柄とTOPIXの推移(2021年初=1.0)
五銘柄とTOPIXの平均と標準偏差を2021年度、2021~2022年度、2021~2023年度、2021~2024年度の四つに分けて算出し、正規分布図に落とし込むと図2のようになります。
図2
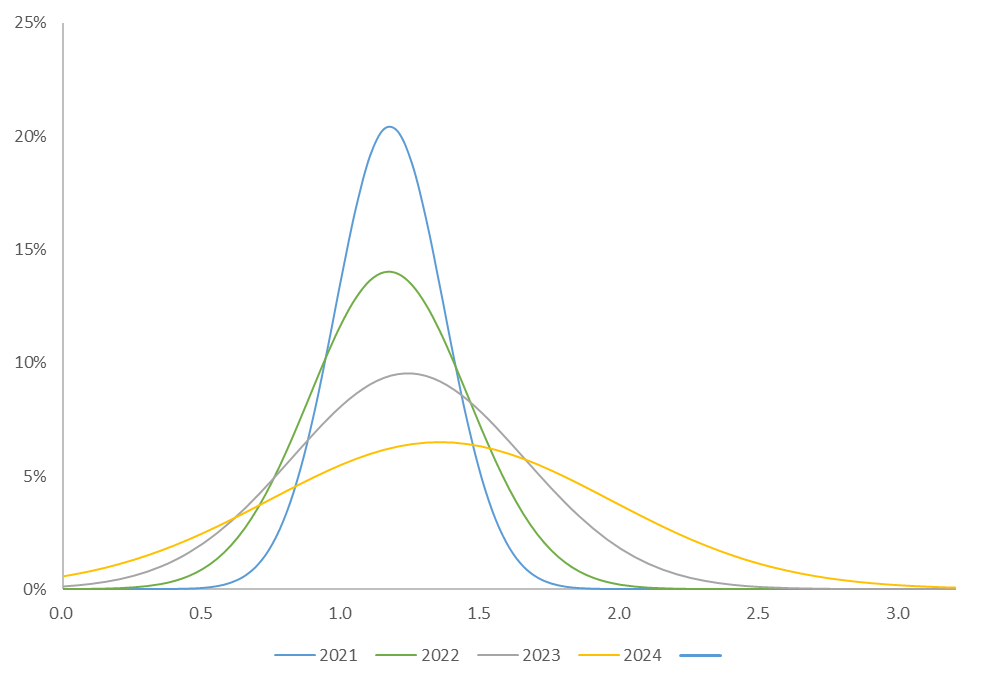
2021~2024年の特定五社の日次終値 出現確率分布の推移
ここまでが、2025年1月6日付のブログですが、本日はさらに発展させて、偏微分方程式(1)のふたつの係数、拡散係数 $D$ と移流係数 $C$ を探り出す作業をしてみましょう。
図3は拡散係数 $D=1.0$ と移流係数 $C=0$ で固定したときの確率分布の推移です。
図3
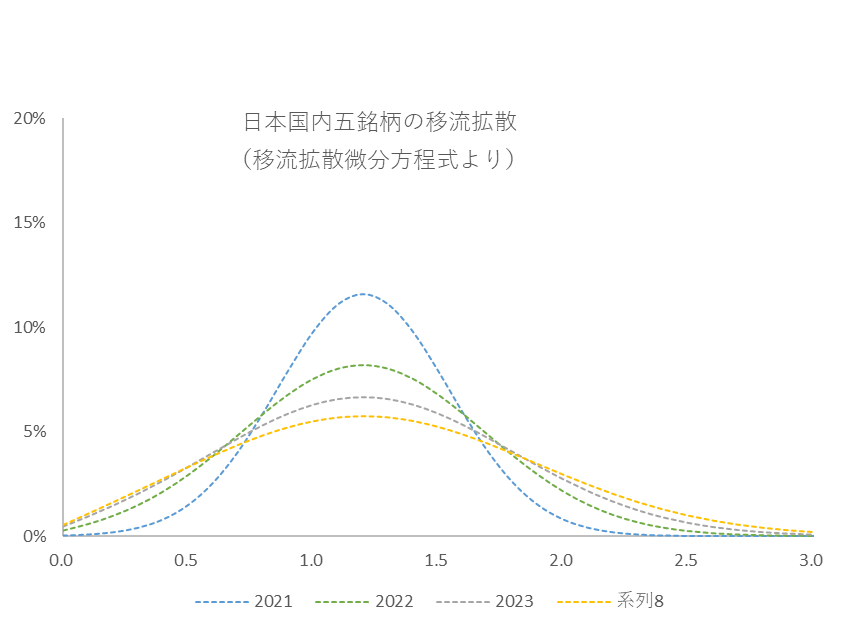
移流拡散微分方程式(1)において拡散係数 $D=1.0$、移流係数 $C=0.0$ のときの確率分布の推移
図3を図2に近づけるためには拡散係数 $D$ と移流係数 $C$ を経過時間とともに変化させる必要があります。では、実際にやってみましょう。各係数を年度別に少しずつ変化させます。各係数が表1になったときの様子が図4です。
表1
| 2021年 | 2022年 | 2023年 | 2024年 | ||
| 移流係数 | C | 0.00 | 0.01 | 0.10 | 0.20 |
| 拡散係数 | D | 0.34 | 0.40 | 0.90 | 1.60 |
図3(理論)が図2(実績)に重なり合う粘度物の移流・拡散係数
図4
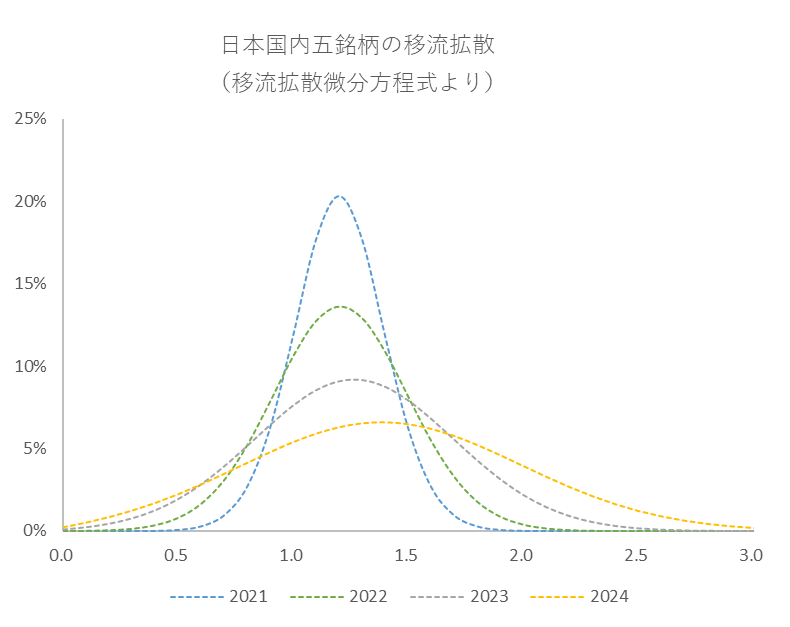
移流拡散微分方程式(1)において拡散係数 $D$と移流係数 $C$ を表1のとおり変化させたときの確率分布の推移
図4は実績を正規分布化して描いた図2と重なり合います。つまり、表1こそが今回探ろうとしていた拡散・移流係数の値です。
ちなみに、移流係数 $C$ がプラスの場合は向かって右方向へ、マイナスの場合は左方向へ移流します。今回、解析の対象としたデータの移流係数 $C$ はすべてプラスですので、右方向へのみ移流しています。
では、同じ要領で世界の株価インデックスの移流・拡散係数を調べてみましょう。
図5
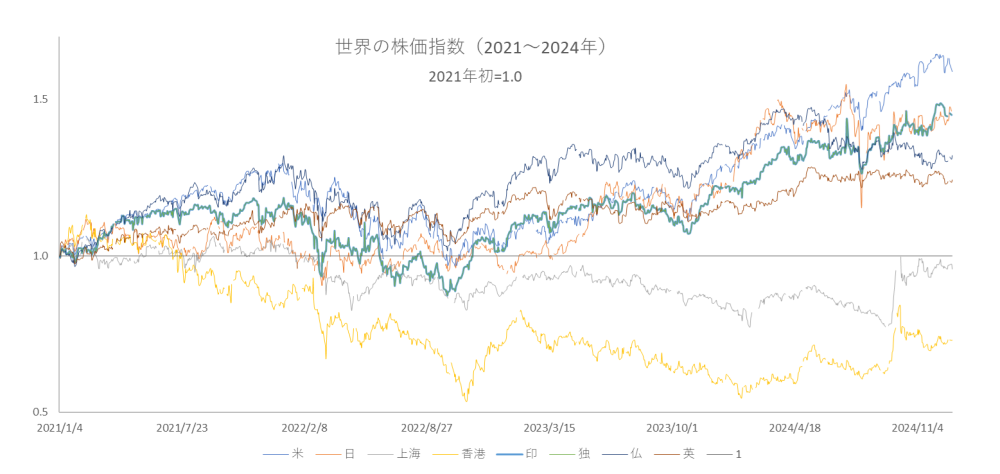
2021年~2024年の世界の株価指数推移(2021年初=1.0)
2021年度、2021~2022年度、2021~2023年度、2021~2024年度の平均と標準偏差を算出して、正規分布図に落とし込むと図6のようなります。
図6
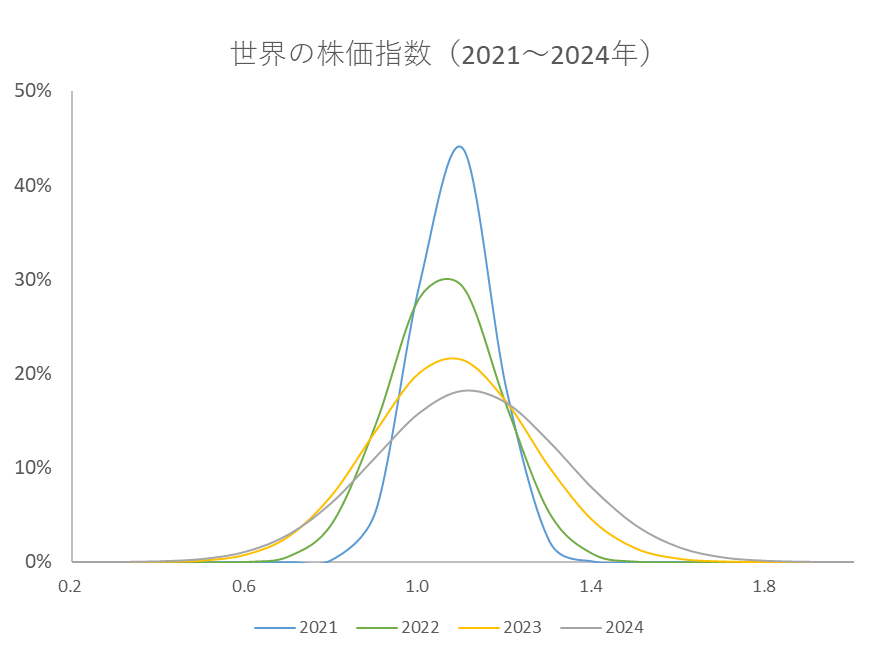
世界の株価指数(日次終値)の出現確率分布の推移(2021~2024年)
次に図3を移流係数 $C$ と拡散係数 $D$ を微調整しながら図6に近づけます。図3が図6にちょうど重なるときのそれぞれの係数は表2のとおりです。
表2
| 2021年 | 2022年 | 2023年 | 2024年 | ||
| 移流係数 | C | 0.00 | -0.05 | 0.10 | -0.07 |
| 拡散係数 | D | 0.40 | 0.00 | 0.33 | -0.20 |
図3(理論)が図6(実績)に重なり合う粘度物の移流・拡散係数
2022年の移流係数と2024年の移流係数と拡散係数がマイナスになっていることに注目してください。マイナスの移流は前年度よりも株価指数の平均が下がったことを意味します。マイナスの拡散は前年度よりも拡散度合いが狭まったことを意味します。株価指数が一進一退を繰り返しながらも徐々に成長、拡散していく様子は図5から視覚的に確認できますが、それを数値化したものが表2というです。
つづく
記事一覧へ戻る