2023年1月23日付けのブログで「ゆらぐ」と「成長が鈍化」する不思議を数理的に解明しました。さっと振り返ると、$r$ を成長係数、$v$ をゆらぎ係数、$B$ をブラウン運動（平均=0、標準偏差= 1の微細なランダム運動）としたとき、株価の変化率は以下の確率微分方程式で表現できます。

$$\frac{dx}{dt}=rx+vx\frac{dB}{dt}\tag{1}$$

$x_{0}$ を初期値とすれば、ある時点 $t$ の株価 $x_{t}$ は、

$$x_{t}=x_{0}e^{(r-\frac{v^2}{2})t+vB}\tag{2}$$

となります。導出方法は上記のブログをご覧ください。

式（2）から明らかなことは、ゆらぎ係数 $v$ が株価の成長を抑制していることです。成長は指数 $r-\frac{v^2}{2}$ の値で決まるからです。そうであれば、このゆらぎ係数 $v$ の実際の値が知りたくなります。これが本日のテーマです。まずは、日本経済全体のゆらぎを探るべく、TOPIX（東商株価指数）を調べてみましょう。図１が過去22年間のTOPIXの推移です。始まりの値が 2001年1月4日の 1280.94、終わりの値が 2023年2月1日の 1972.23 です。

図１

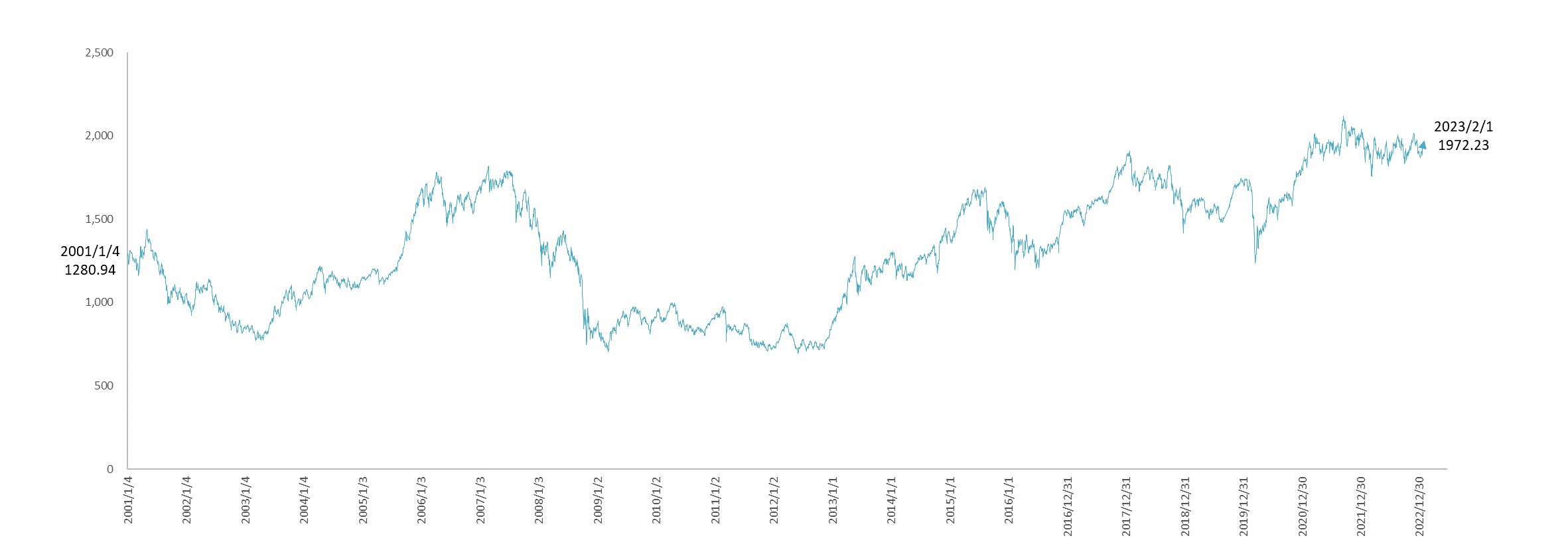
過去22年間（2001年1月4日から2023年2月1日）の TOPIX（東商株価指数）の終値推移

始点=1280.94、終点=1972.23

 

ここで、ゆらぐことなく始点から終点へ推移したとします。

図２

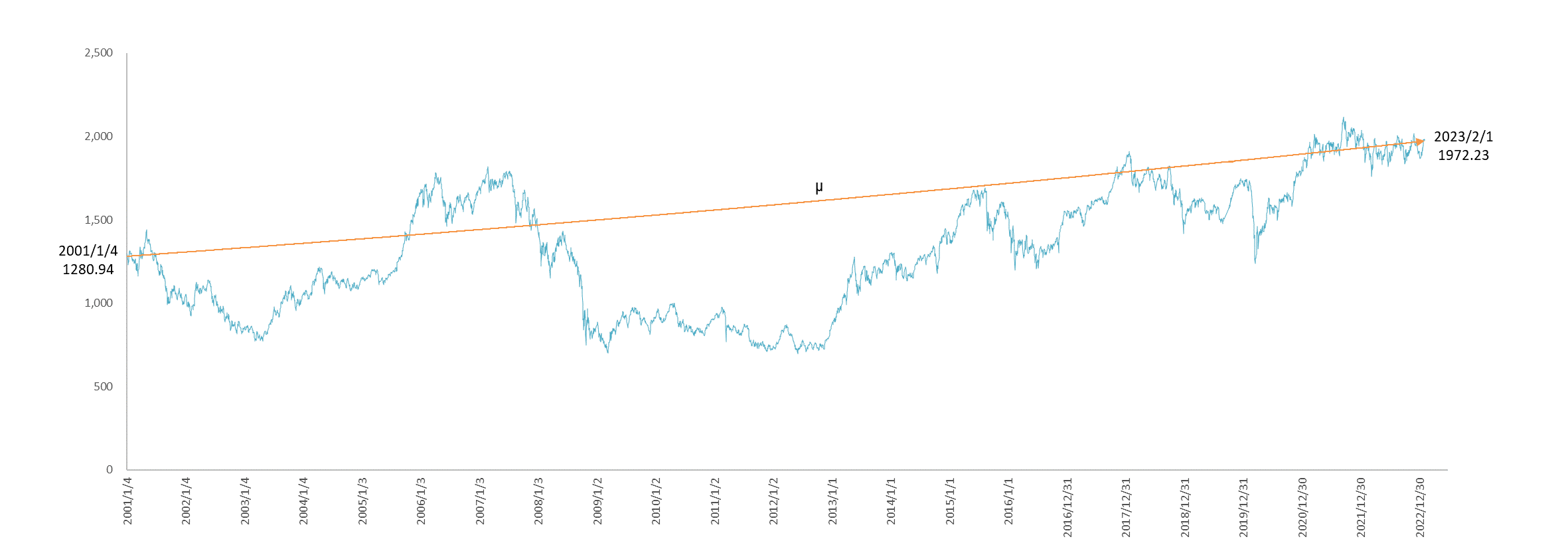
「ゆらぎ」がないときの成長がオレンジの線（μ）

 

オレンジの線（μ）が、始点の 1280.94 が 5405回の取引を経て終点 1972.23 へゆらぐことなく増加したときの曲線です。一日の成長率を $α$ とすると、

$$1280.94\cdot{e^{α\cdot{5405}}}=1972.23\tag{3}$$

ですから、これを $α$ について解くと、$α=0.000079846=7.9846\cdot{10^{-5}}$ であることがわかります。

一方、式 (2) から「ゆらぎ」の原因であるブラウン項 $vB$ を取り除くと、

$$x_{t}=x_{0}e^{(r-\frac{v^2}{2})t}\tag{4}$$

となります。これが、図２の μ 線と一致するはずですから、 µ 線は、

$$x_{t}=1280.94e^{7.9846\cdot{10^{-5}}t}\tag{6}$$

であるべきです。次に知りたいのはゆらぎの範囲です。図２をみればわかるとおり µ 線 を中心にしたランダムな上下運動がゆらぎですから、この上下動の可動域を図２に書き込める数式が欲しいところです。式 (7) をご覧ください。

$$x_{t}=1280.94e^{7.9846\cdot{10^{-5}}t\pm{v}\sqrt{t}}\tag{7}$$

ゆらぎ係数 $v$ の前の符号がプラスのときは上側、マイナスのときは下側の範囲を示します。また、$v$ の値を変えることでその可動域を自由に調整することができます。図３は $v$ の値を、0.01、0.015、0.02 の三通りで計算したときのゆらぎの範囲です。

図３

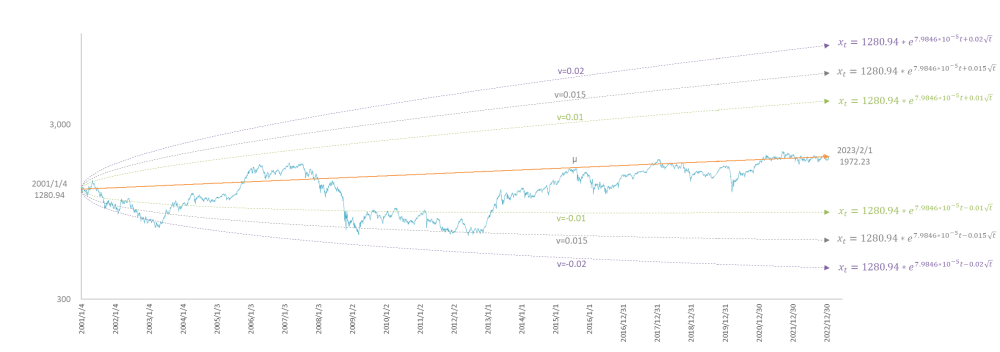
v=0.01, 0.015, 0.02 の三通りで計算した TOPIX のゆらぎ幅。縦軸は対数。

 

三通りのゆらぎ幅でもっとも実績にフィットしているのは $v=0.015$ ですから、これをTOPIXのゆらぎ係数と認定しましょう。

図４

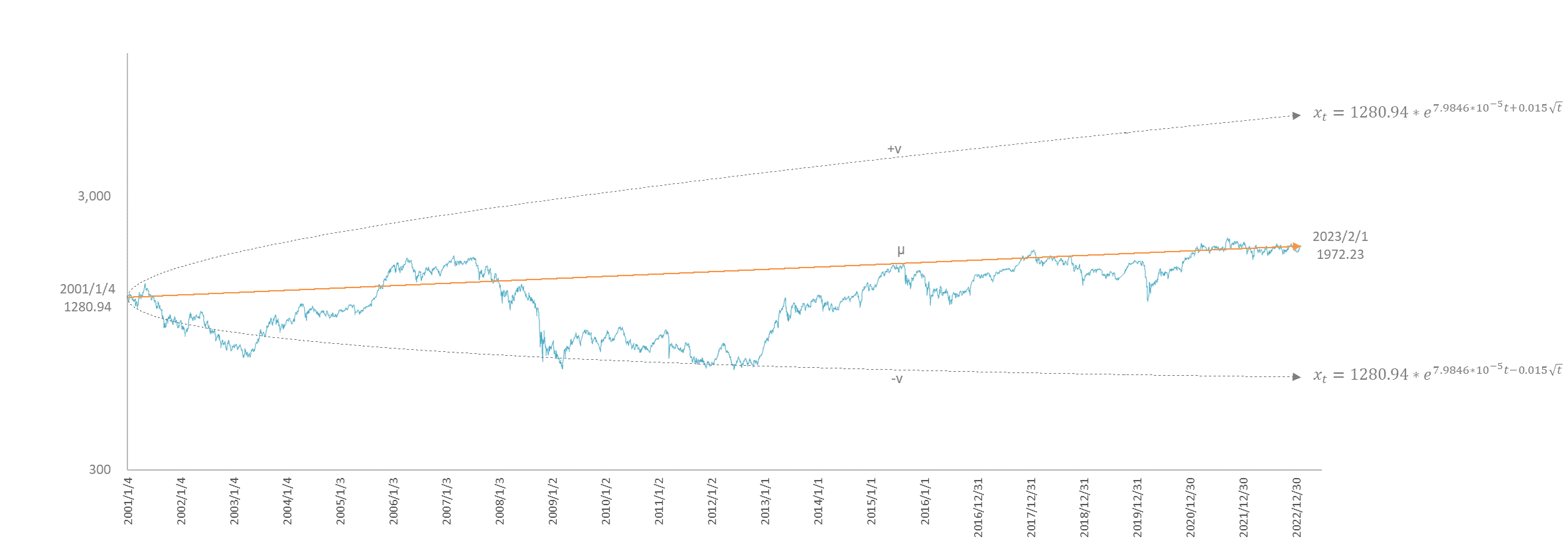
TOPIXのゆらぎ幅は $v=0.015$ のときに実績のゆらぎにもっともフィットする。

ゆらぎの範囲が破線 $x_{t}=1280.94e^{7.9846\cdot{10^{-5}}t\pm{0.015}\sqrt{t}}$ によって表示されている。

 

上下の破線ですが、上側の曲線を単に $+v$ 線、下型の曲線を $-v$ 線と呼ぶことにします。そしてそれは以下の数式で表されます。

$$x_{t}=1280.94e^{7.9846\cdot{10^{-5}}t\pm{0.015}\sqrt{t}}\tag{8}$$

ところで図４は始点が 2001年1月4日にとっていますが、ゆらぎが式 (8) で計算、図示できることがわかれば、始点をどこにとってもよいはずです。では、ここで時間を 2001年1月4日に戻してみましょう。もちろんそこから先はどうゆらぐかはわかりません。但し、係数はさきほどと同じ手続きで計算されているものとします。そうすると便利なゆらぎ式 (8) を使って計算すれば、おおよそ図５の範囲でゆらぐであろうと予測できます。

図５

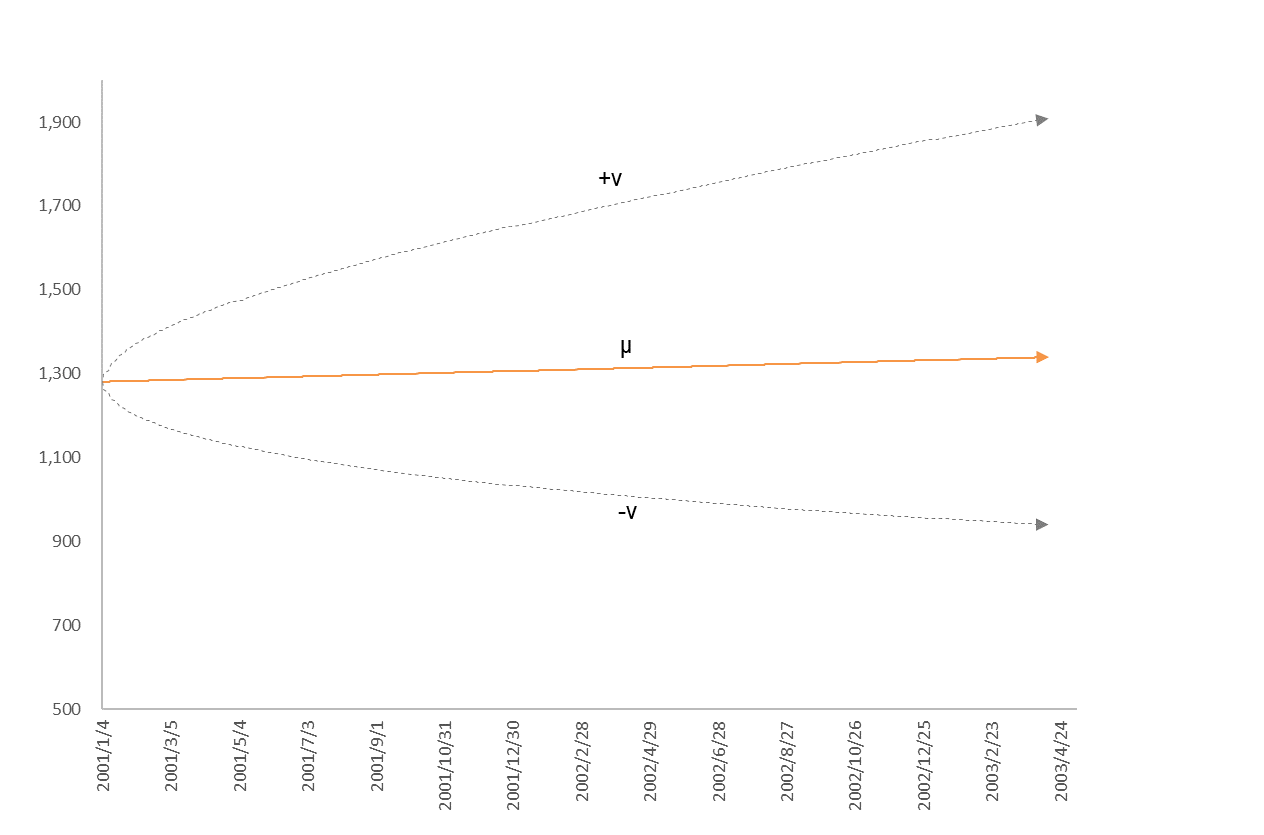
2001年1月4日のTOPIX終値を始点としたときのゆらぎの予測範囲

 

では、実際はどうだったでしょうか？

図６

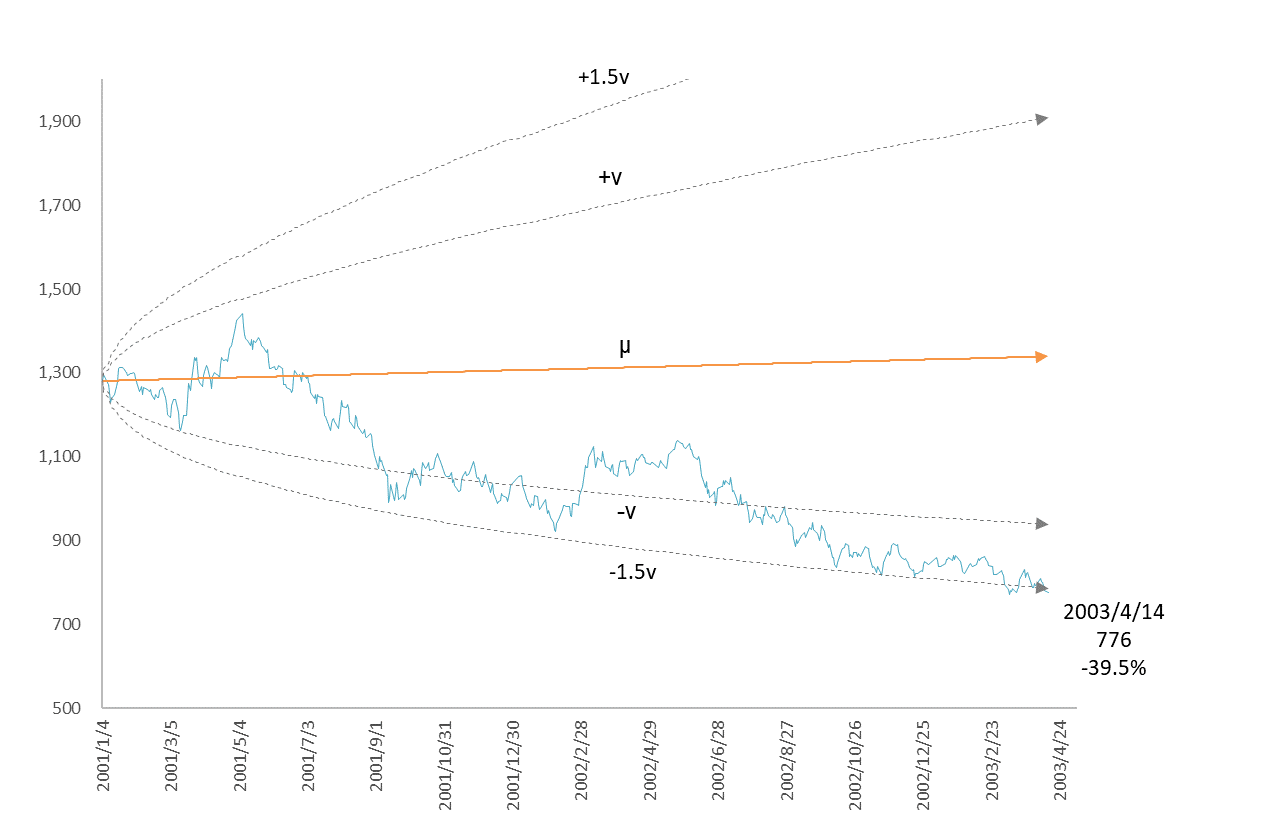
2001年1月4日～2003年4月14日のTOPIXのゆらぎ実績

 

ほぼ、$-v$ 線 に沿ってゆらいでいます。ここで、式 (8) にゆらぎ倍率□を付け加えます。

$$x_{t}=1280.94e^{7.9846\cdot{10^{-5}}t\pm{□v}\sqrt{t}}\tag{9}$$

そして、$\pm{v}$ 線の始点と終点（＝次の始点）を実績に合わせるために□に値を入れながら微調整します。図６は□に $-1.5$ を代入したときのものです。こうすることで短期のゆらぎトレンドを数値化することができます。

ところで、時間経過とともに始点は右方向へ移動します。始点はどこにでも設定することができますが、ゆらぎの節目にあたる点、つまり下降トレンドから上昇トレンド（谷）、上昇トレンドから下降トレンド（頂）への変換点に設定し、□の値を調整して始点から次の始点に $\pm{v}$ 線が向かうようにしたものが図７です。％は谷から次の頂、または頂から次の谷までの変化率です。

図７

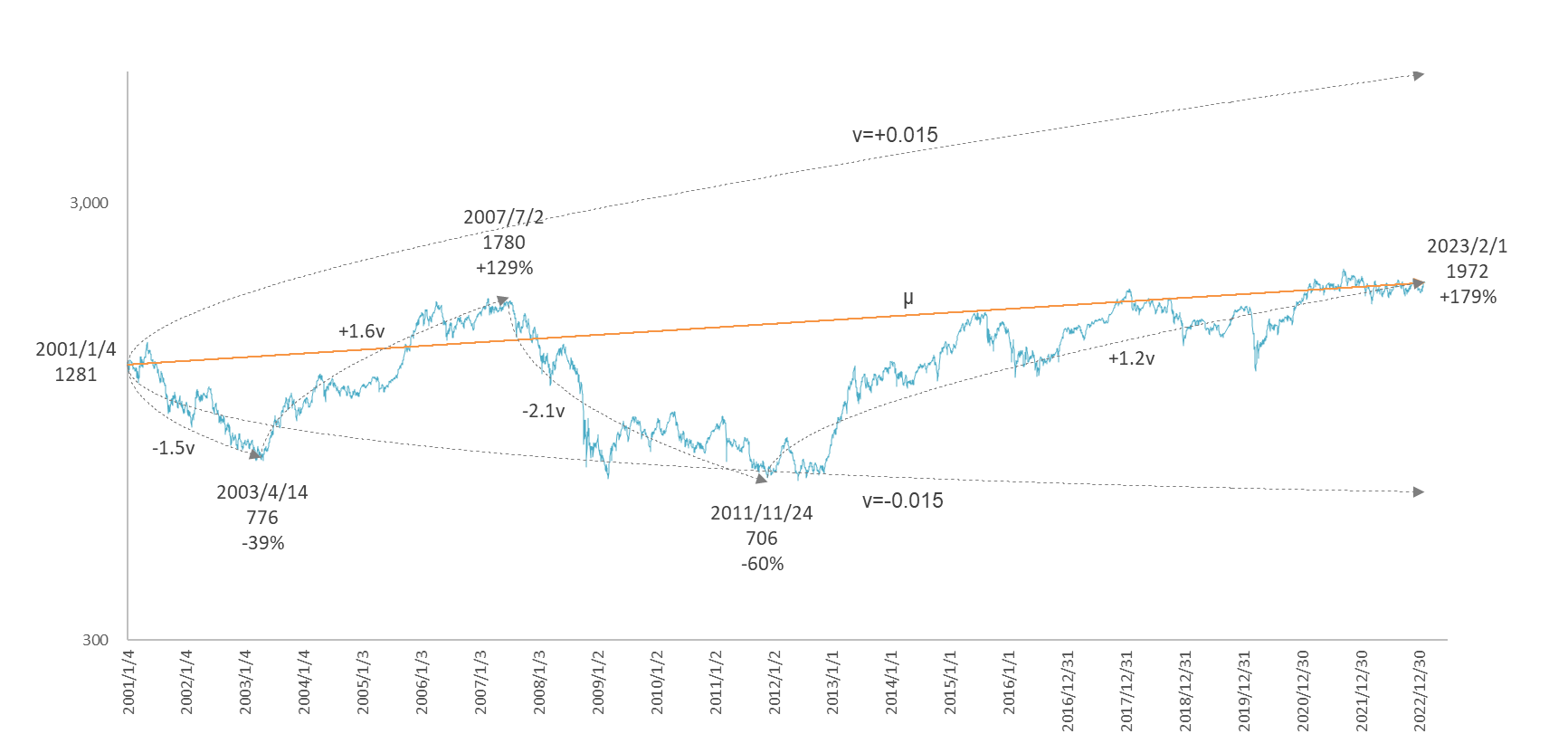
TOPIX の長期ゆらぎ係数 $v=\pm{0.015}$と短期ゆらぎ。％は始点間の変化率

 

ここで比較のため米国の代表的な株価インデックスである S&P500 を取り上げます。TOPIXと同様のプロセスを踏んで得られるゆらぎ係数は、おおよそ$v=\pm{0.02}$です。日本は2008年のリーマンショックからの回復が遅れ、$+1.2v$ の上昇ゆらぎで同ショック底値の1.8倍までしか回復していないのに対して、米国は同ショック直後から着実に回復を続け、 $+1.9v$ の上昇ゆらぎで5倍になっています。

図８

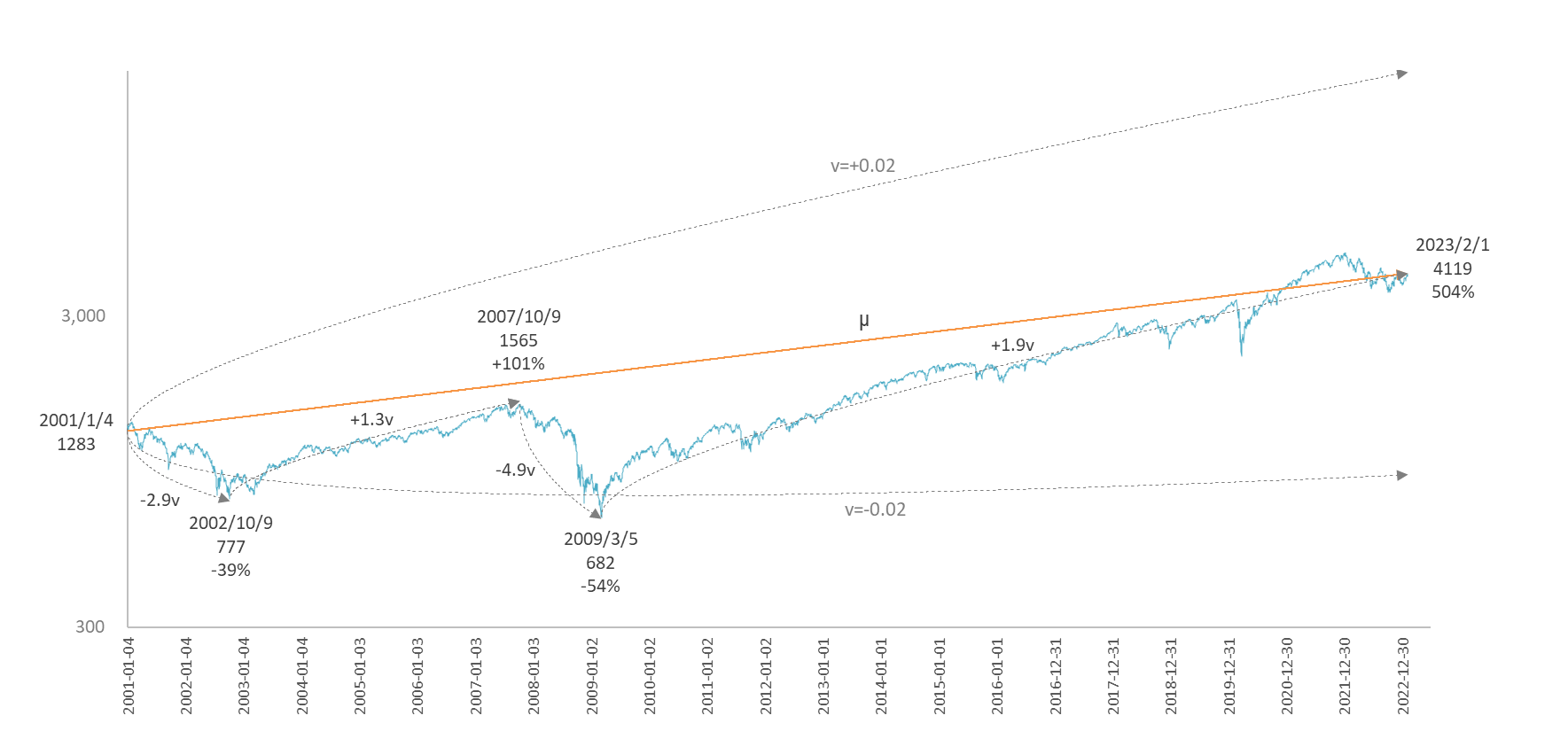
S&P500 の長期ゆらぎ係数 $v=\pm{0.02}$と短期ゆらぎ。％は始点間の変化率

 

図７（TOPIX）と図８（S&P500）をズームインして直近の五年間に範囲を絞ったものが図９（TOPIX）と図10（S&P500）です。

図９

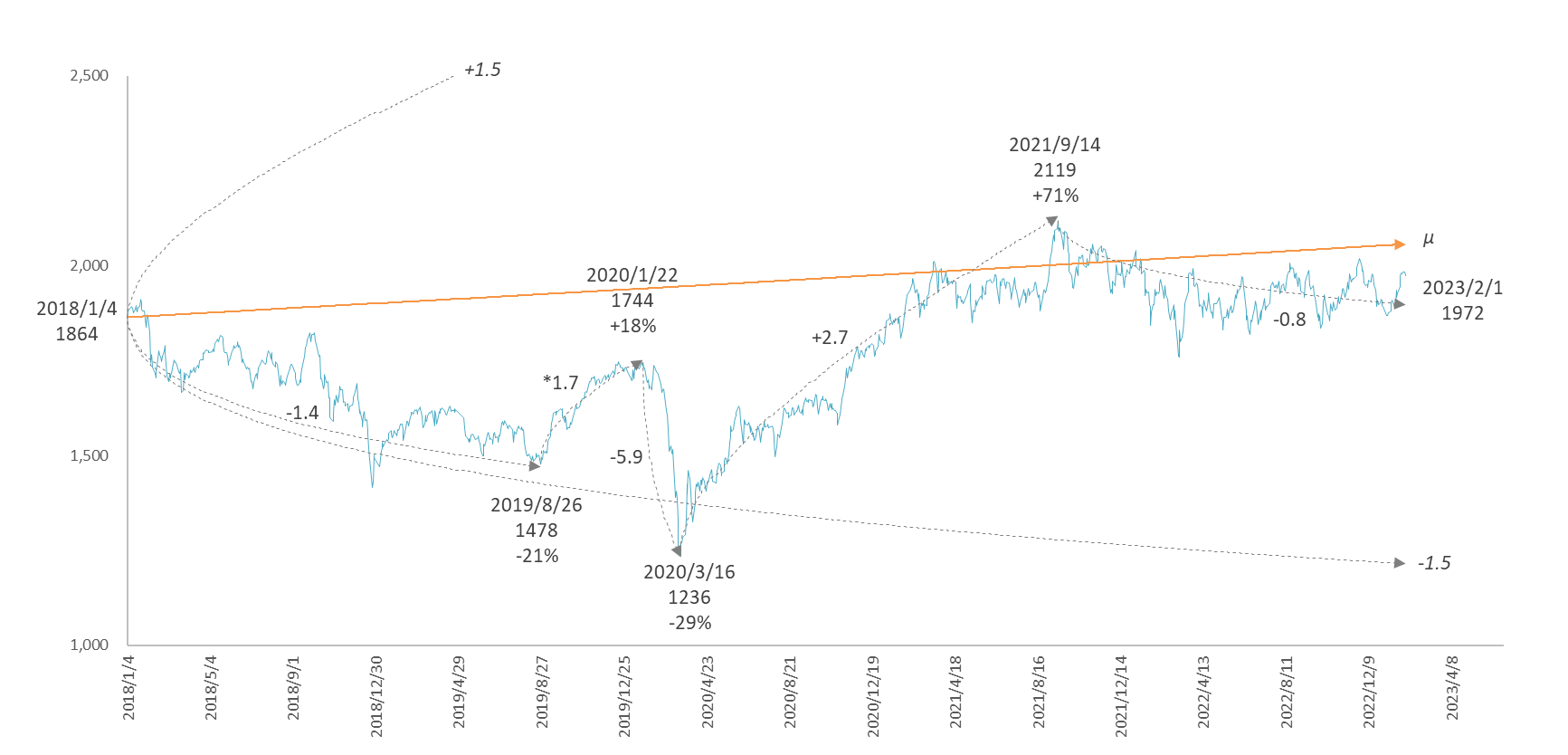
TOPIX 直近五年間のゆらぎ係数。％は始点間の変化率。

始点間のゆらぎ係数 = インデックス固有のゆらぎ係数（$v=\pm{0.015}$）ｘ 調整倍数（式(9)の□）x 10²

 

図10

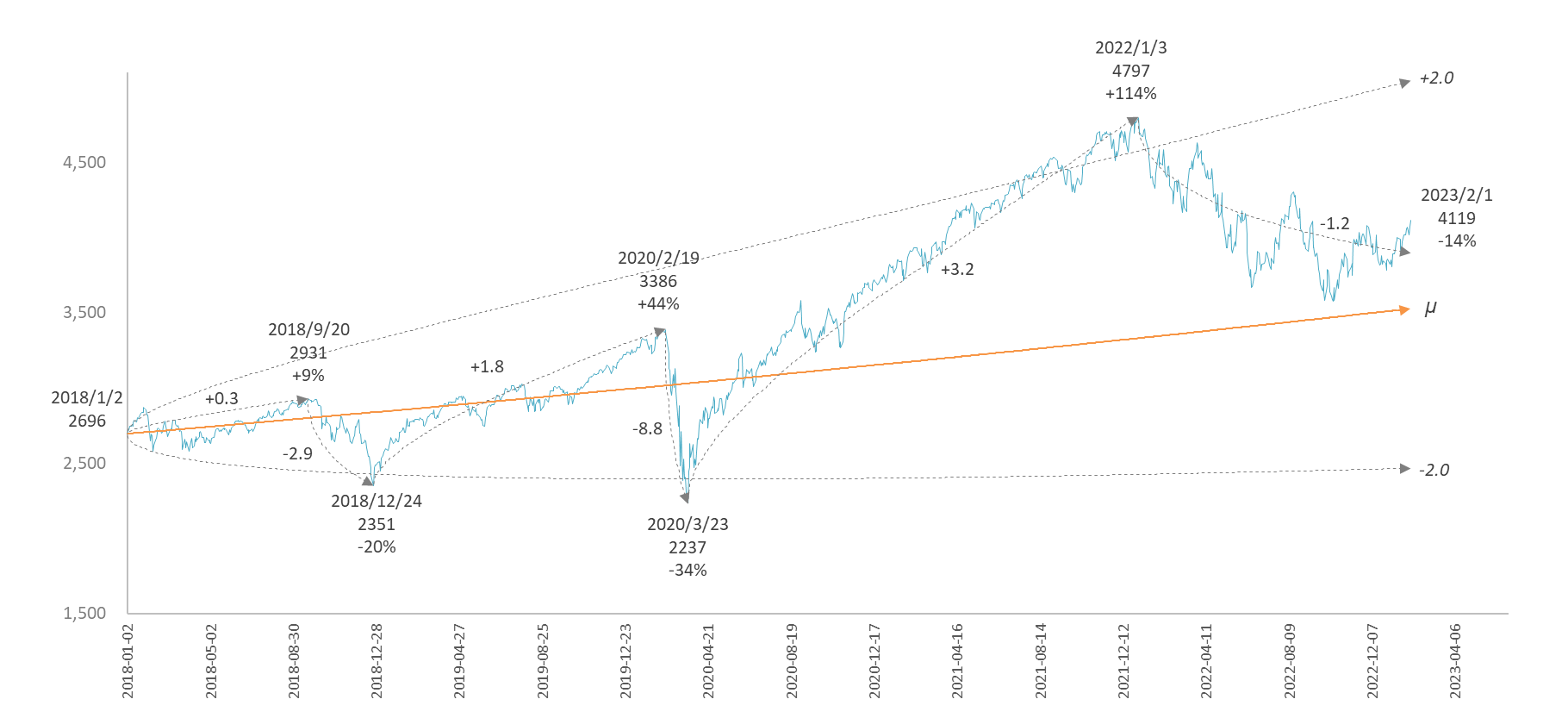
S&P500 直近五年間のゆらぎ係数。％は始点間の変化率

始点間のゆらぎ係数 = インデックス固有のゆらぎ係数（$v=\pm{0.02}$）ｘ 調整倍数（式(9)の□）x 10²

 

ふたつのインデックスのゆらぎを対等に（同じスケールで）比較するため、それぞれのゆらぎ係数 $v$ （TOPIXなら $0.015$、S&P500なら $0.02$）を調整倍（式（９）の□、図８の $-2.9, +1.3,\cdots$）して、さらに比較しやすいように100倍した数値を表記しています。

$$始点間のゆらぎ係数=インデックス固有のゆらぎ係数\pm{v}ｘ調整倍率（式(9)の□）ｘ10^{2}\tag{10}$$

図９と図10 を比較すると、以下のようなことがわかります。

①　TOPIXは2018年から $μ$ 線を下回るトレンドのまま2020年のコロナショックに突入し、2021年に $μ$ 線に回復するまでに3年を要した。2018年初の株価 1864 は、2023年2月1日現在、1972 とわずか 6％ の成長にとどまっている。コロナショックの谷から次の頂までのゆらぎ係数は +2.7 (固有ゆらぎ係数 0.015 x 調整倍率 1.8 x 100）で、期間は18か月。

②　一方、S&P500は、$μ$ 線に沿って堅調に推移し、コロナショックで急降下するも、その後はあっという間に $μ$ 線を突き抜ける回復力を示した。結果、2018年初の株価 2696 は、2023年2月1日現在、53% 成長して 4119 になっている。コロナショックの谷から次の頂までのゆらぎ係数は +3.2 (固有ゆらぎ係数 0.02 x 調整倍率 1.6 x 100）で、期間は22か月。

③　始点間のゆらぎ係数 式(10）は、いずれのインデックスもさまざまな値をとりながら正負を繰り返す。正→負→正の三本の矢印を繫ぐと「N字」に見えるので、株価は絶えず「N字」成長 を繰り返しているともいえる。その様子を集計したものが表１。① 「ゆらぎ係数」は式（10）で得られたゆらぎの度合い、② はそのゆらぎが継続した期間（単位：年）、③ 「加重ゆらぎ係数」は①と②の積。

表１ー１　TOPIX

① ゆらぎ係数	② 継続期間（年）	①*② 加重ゆらぎ係数
-1.4	1.5	-2.0
1.7	0.4	0.7
-5.9	0.3	-1.8
2.7	1.6	0.7
-0.8	1.4	-2.0

 

表１ー２　S&P500

① ゆらぎ係数	② 継続期間（年）	①*② 加重ゆらぎ係数
0.3	0.8	0.3
-2.9	0.3	-0.9
1.8	1.2	2.2
-8.8	0.1	-0.9
3.2	1.8	5.7
-1.2	1.0	-1.2

 

 

株価は絶えず 正→負→正 の N字成長 を繰り返す。

 

表１をプラス成長とマイナス成長に分類、集計したものが表２。

表２－１

TOPIX	ゆらぎ係数（平均）	継続期間（年、累計）	加重ゆらぎ係数（累計）
プラス成長	2.2	2.0	5.0
マイナス成長	-2.7	3.2	-4.8

 

表２－２

S&P500	ゆらぎ係数（平均）	継続期間（年、累計）	加重ゆらぎ係数（累計）
プラス成長	1.8	3.8	8.1
マイナス成長	-4.3	1.4	-3.0

 

 

株価の長期的なパフォーマンスは「加重ゆらぎ係数」に大きな影響を受ける。

 

加重ゆらぎ係数に注目してください。TOPIXがプラス成長 5.0、マイナス成長 -4.8 であるのに対して、S&P500 はプラス成長 8.1、マイナス成長 -3.0 です。直近の五年間、TOPIXはほぼ現状維持、S＆P500は五倍増、というふたつのインデックスのパフォーマンスの極端な違いは、この加重ゆらぎ係数の差異によるものです。

 

つづく

記事一覧へ戻る