一定の需要がある商品を、在庫がゼロになる直前に一定の単位数量で発注する場合を考えてみましょう。

実例をみるとわかりやすいので以下のように仮の数字をおいてみます。

発注単位＝1,000

保管料＝10円/商品

発注手数料＝5,000円/回

月間需要＝200（一定）

上記の前提で、月々の保管料と発注手数料がどのように発生するかを確かめてみると表１のようになります。

表１

発注単位=1,000、保管料=10円/商品、発注手数料=5,000円/回の場合の年間経費

 

この場合の年間経費は9万3千円です。保管料が安ければ発注単位を大きくした方がよさそうですし、発注手数料が高ければ、発注回数を減らしたら方がよさそうです。発注単位を小さくすれば保管スペースも少なくてすみますが、発注回数が増えて手数料も増えます。果たして、発注単位数量をどこに設定したら総経費が最も安くなるのでしょう？これを計算で求める方法を探るのが本日のテーマです。

では早速、数式化に取り組みます。知りたい発注単位数量を $x$ とおきます。発生する経費は以下のふたつです。

商品1単位あたりの保管料：$a$

発注手数料：$b$

ひと月の需要を $c$ とすると、発注回数は需要を発注単位で割ればいいので、

$$\begin{array}{}\text{(1)}& \frac{c}{x}\end{array}$$

です。仕入れてから次に発注するまでの平均在庫数量は、需要（出荷）が一定なので

$$\begin{array}{}\text{(2)}& \frac{x}{2}\end{array}$$

とおけます。ひと月の保管料は、平均在庫数量に単位商品あたりの保管料を掛ければいいので、

$$\begin{array}{}\text{(3)}& \frac{ax}{2}\end{array}$$

です。一方、ひと月の発注手数料は発注手数料に発注回数を掛ければいいので、

$$\begin{array}{}\text{(4)}& \frac{bc}{x}\end{array}$$

となります。よって、経費の合計は、

$$\begin{array}{}\text{(5)}& \frac{ax}{2}+\frac{bc}{x}\end{array}$$

となります。式 $(5)$ は発注数量 $x$ の関数ですので、これを $f(x)$ とおくと、

$$\begin{array}{}\text{(6)}& f(x)=\frac{ax}{2}+\frac{bc}{x}\end{array}$$

知りたいのは $f(x)$ を最小にする「最適仕入れ数量」である $x$ ですから、式 $(6)$ を $x$ で微分します。

$$\begin{array}{}\text{(7)}& f^{\prime }(x)=\frac{a}{2}-\frac{bc}{x^2}\end{array}$$

$f^{\prime }(x)=0$ とおけば、最適仕入れ数量は

$$\begin{array}{}\text{(8)}& x=\sqrt{\frac{2bc}{a}}\end{array}$$

と決まります！

式 $(8)$ に表１で使った $a$、 $B$、 $c$ の値を代入すると、最適仕入れ数量は、

$$\begin{array}{}\text{(9)}& x=\sqrt{\frac{2\ast 5000\ast 200}{10}}=447\end{array}$$

と決まります。

ところで式 $(6)$ は実際どのような形をしているのでしょうか？図１をご覧ください。

図１

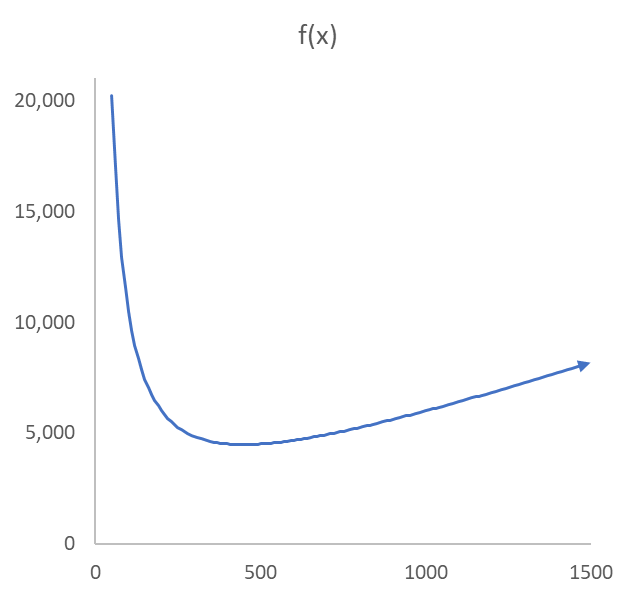
$f(x)=\frac{10x}{2}+\frac{5000\ast 200}{x}$ 

縦軸が経費 $f(x)$、横軸が発注単位 $x$

 

確かに 発注単位が500の手前で経費が最小になっています。そこは上曲線の接線の傾き、すなわち $f(x)$ の微分　$f^{\prime }(x)$ がゼロになる場所です。図２が図１の微分（接線）曲線です。これによって正確に $x=447$ のときに $f^{\prime }(x)=0$ となることが分かります。

図２

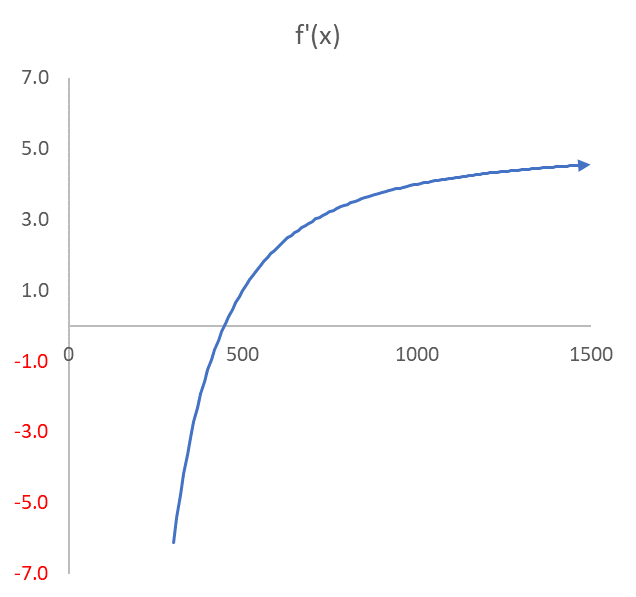
$f^{\prime }(x)=\frac{10}{2}-\frac{5000\ast 200}{x^2}$ 

縦軸が図１の接線の傾き、横軸が発注単位 $x$

$x=447$ で接線の傾きがゼロになる。

 

ちなみに、表２が他の組み合わせを式 $(8)$ で計算した結果です。

表２

 

「微分」の威力、すごいです。

 

おわり

 

参考文献：社会現象の数理解析（微分・積分と現象のモデル化）、河野光雄著、中央大学出版部、2000

 

 

 

記事一覧へ戻る