「量子」とは、光子や電子のように、超ミクロなもののことで、その最大の特長は「粒」であると同時に「波」であるという点です。目に見えないのになぜそんなことがわかるのか?という疑問がすぐに湧きますが、過去に実験(図1)を通じて証明されていますので、まずは受け入れましょう。
次に、その量子には、「その場所と運動量が同時に測定できない。」という不思議な性質があります。どちらか一方を測定するともう一方が不確定になります。我々が日常目にする物体ではそのどちらも同時に測定することができるのに、量子ではそれができないということです。これまた違和感しかありませんが、これも実験で確認されていますので受け入れましょう。
ここで、話を飛躍させて「量子」を「株価」に置き換えてみます。そうすると上に述べたことは、
1) 株価は「粒」であり「波」である。
2) 「株価」と「その方向・勢い」は同時にはわからない。
となります。
1) 株価は「粒」であり「波」である。
まず、量子である電子から。下の四枚の写真は電子を一秒間に10個のスピードで、20分間飛ばし続けた結果、検出器にあらわれる模様です。最初はランダムな白点としか見えないのですが、数が多くなると縞模様が見え始めます。波の山と谷が干渉し合ってできる干渉縞です。波特有の現象で、不思議ですが、これが電子は粒子であり、波でもあるという証拠です。
図1

電子の 二重スリット実験(日立のウェブサイトより)
次は株価。東証一部の全銘柄の平均株価であるTOPIXを一日四回(始値、高値、安値、終値)観測した結果を並べたものです。
図2
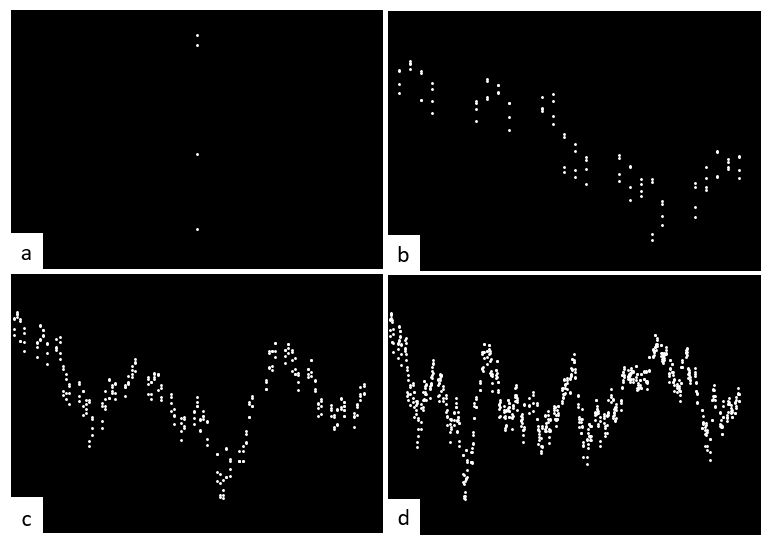
2022年1月4日~10月27日のTOPIX (a=4個、b=100個、c=300個、d=800個)
四個セットの白点が日数の経過とともに波をつくっていくのがわかります。観測した瞬間はわかりませんが、観測データを集めるとその「瞬間データ」が波の一部を構成していることがわかります。これもよく考えてみると不思議な現象です。
2) 「株価」と「その方向・勢い」は同時にはわからない。
もし、これが同時にわかるのであれば、世の中、株で儲ける人だらけになってしまいます。といいますか、もし同時に分かるのであれば株価の売買そのものが成立しないので、原理的にあり得ません。売る人と買う人がいてこそ株価が決まります。そして、決まったからといって、次にそれが上がるのか下がるのか、どのくらい動くかはその瞬間にはわかりません。つまり、「株価」とその「動きの方向と度合い」を同時に測定することはできないのです。
以上、確かに「株価」は「量子」と性質が似ているようです。
さて、ここからが本題です。物理学には実際の観測結果を説明し、その後の動きも予測できる「数式」があります。目に見えるものを対象とする古典力学は、たとえばパラシュート降下で何秒後にどこまで落ちるか?など、その数式によって確定的に予測することができますし、目に見えない超ミクロな世界を対象とする量子力学は、確率的に予測することができます。
量子は粒子でもあり波でもあるといいましたが、そのふたつを結びつける数式を見つけた天才がいます。そのひとりがシュレディンガーで、
$$\hat{H}\psi=E\psi\tag{1}$$
がその方程式です。これだけ?という感じですが、$\hat{H}$ はハミルトニアン、$\psi$ は波動関数、$E$ がエネルギーです。だったら「ハミルトニアン=エネルギー」ということ?と誰しもが思いますし、ハミルトニアンって何やん?というのも、当然の質問です。そこでその中身をのぞいてみると、式 $(1)$ は、
$$-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\psi=E\psi\tag{2}$$
なのだそうです。$\hbar$ はエイチ・バーと読み、プランク定数 $h$ を $2π$ で割ったもの 、$m$ は粒子の質量ですから、$-\frac{\hbar^2}{2m}$ は定数です。次の $\frac{\partial^2}{\partial x^2}\psi=E\psi$ は、この微分方程式の解が「二回微分すると元の関数の定数倍となる関数」であることを示しています。三角関数のサインは一回微分するとコサインになり、コサインを微分するとマイナス・サインになります。よってサインは二回微分するとマイナス一倍になるので要件を満たしています。
導出はすっとばして結果だけみましょう。
$$\psi=\sqrt{\frac{2}{L}}\sin\frac{n\pi}{L} x\tag{3}$$
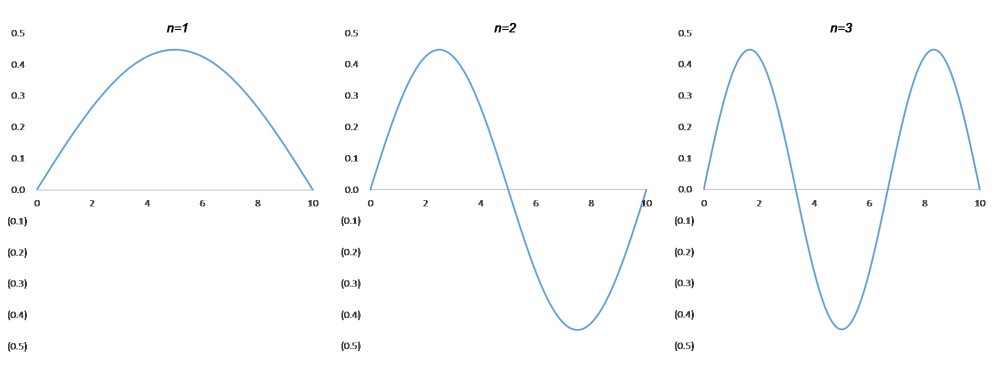
確かに、サイン関数になっています。$\sqrt{\frac{2}{L}}$ は波の高さ、$\frac{n\pi}{L}$ は波の数です。式 (3) は「波動関数」と呼ばれていて $\psi$(プサイ)で表されます。ここで、粒子が $x=0~10$ の間に閉じ込められている状態、つまり、$L=10$ として、$n=1, 2, 3$ の三パターンを計算すると、
図3
L=10 のときの波動関数。左から, n=1,2,3
となります。$n$ の数に波の数が対応しています。サイン波ですから正と負の値を行ったり来たりしますが、今、我々が知りたいのは量子の存在確率ですから、二乗して正の値にしましょう。
図4
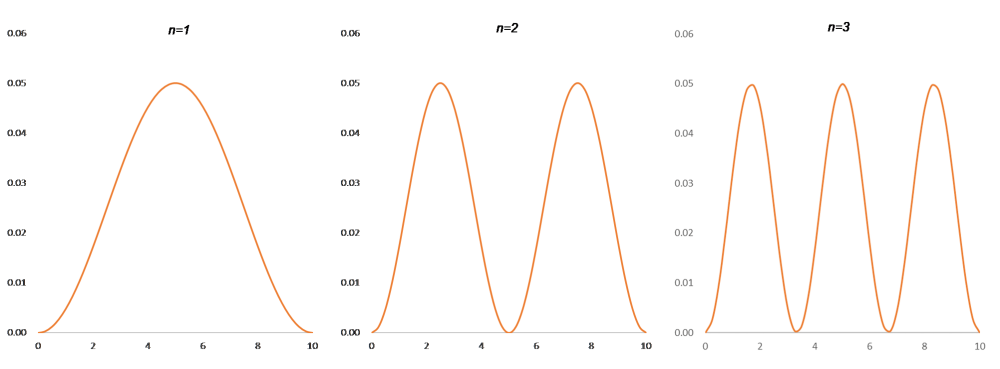
L=10 のときの波動関数の二乗。左から、n=1,2,3
不思議ですが、波動関数 $\psi$ を二乗した波の面積(横軸と曲線に囲まれた面積)は $1$ になります。つまり、図5がまさに量子の存在確率を表している、ということです。
$n=1$ のとき、中央($x=5$)で観測される確率が最も高く、$x=5±2$ の間で観測される確率は七割以上あります。一方、$n=2$ のときは、中央の $x=5$ で観測されることはなく、$x=2.5$ と $x=7.5$ の周辺で観測される確率が増えます。$n=3$になると、量子が観測されやすい場所は$ x=1.75, 5.00, 8.25$ の三か所になります。
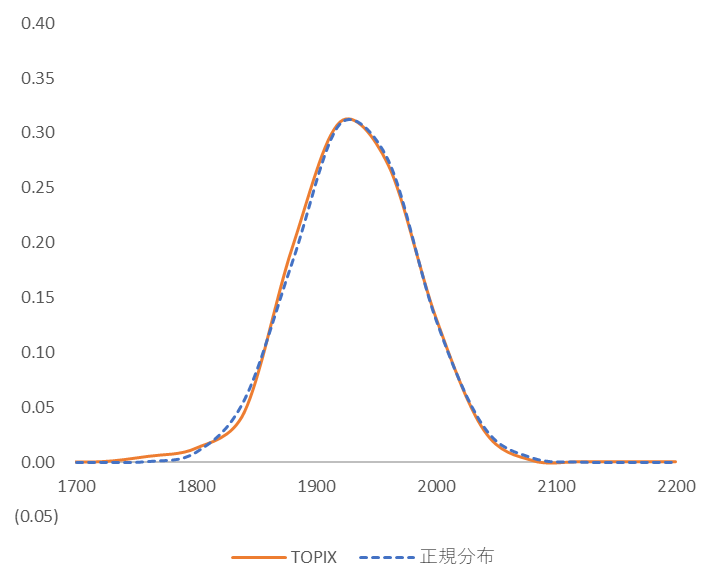
ではここで、実際に株価はどのように分布しているかをみましょう。図5は図2d を出現確率分布に書き換えたものです。
図5
TOPIX の出現頻度(2022年1月4日~10月27日)
データ刻み幅=40 のヒストグラム(オレンジの線)と正規分布(平均=1933、標準偏差=50 の青の破線)
オレンジの線が実績ですが、図4の 量子存在確率分布 $n=1$ に確かに似ています。また、その形はほぼ正規分布(青色の破線)で近似できることもわかります。
では、量子存在確率分布 $n=2$ の「二こぶラクダ」パターンもあるでしょうか?なかなか探すのが難しいのですが、ありました!
図6
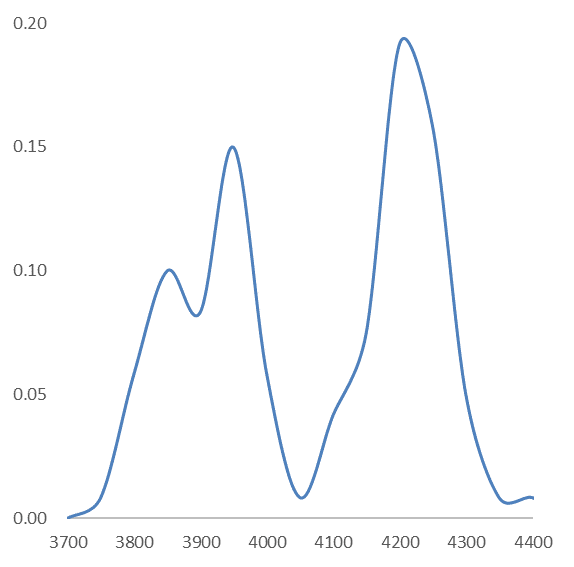
2021年1~6月の S&P500(終値)の出現確率分布
2021年前半の S&P500(終値)の出現確率分布です。なぜ、二こぶになったのか、株価チャートで確認してみると、
図7
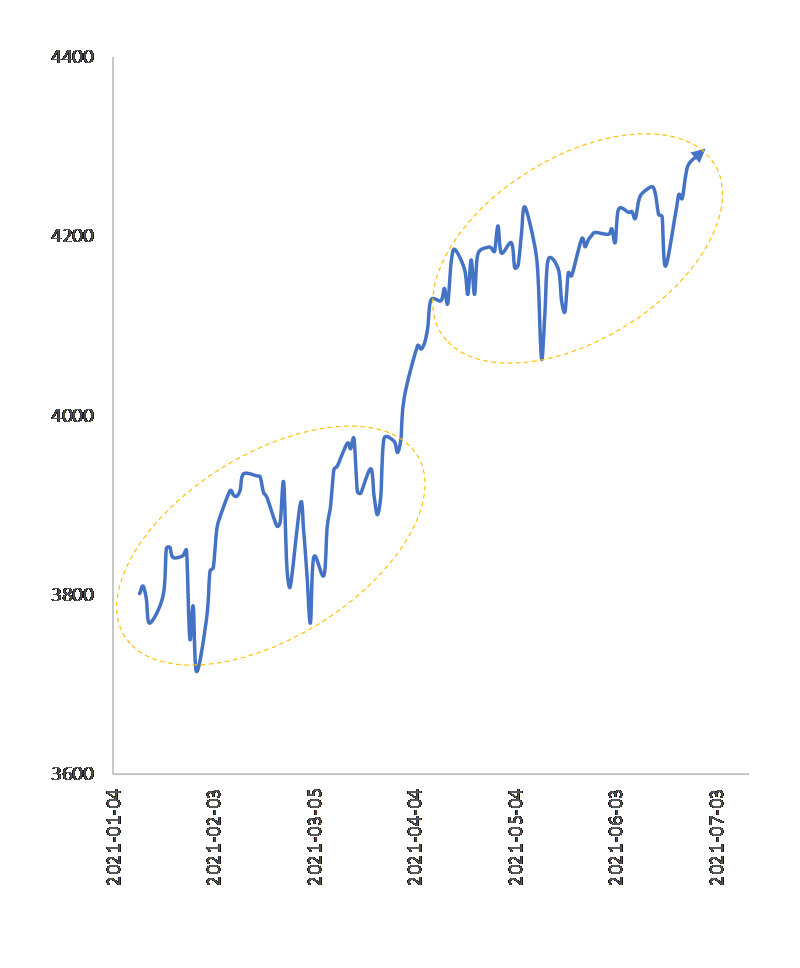
2021年1~6月の S&P500(終値)のチャート。4月に $n=1$ から $n=2$ へ励起。
となっていて、2021年4月から5月にかけて株価がジャンプ・アップしているのがその理由です。これは量子が $n=1$ から $n=2$ のエネルギー状態へ励起する現象(図4)に似ています。
事例をもうひとつ。
図8
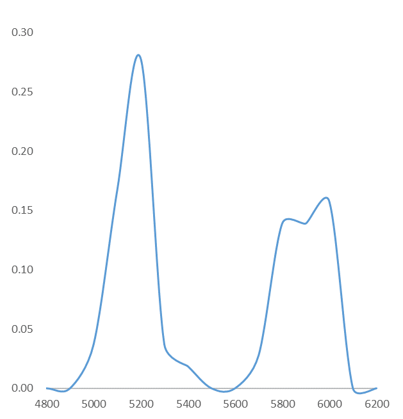
2022年10月20日~同年11月30日の資生堂(始値、高値、安値、終値)の出現確率分布
図9
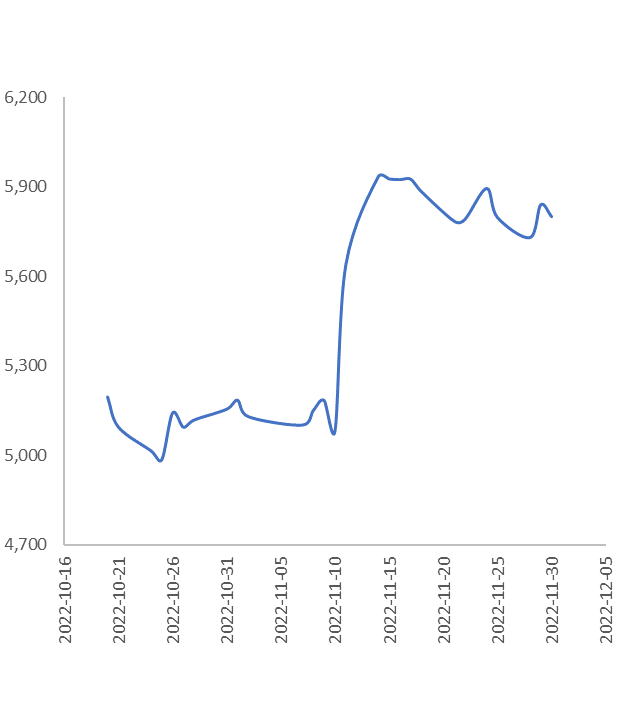
2022年10月20日~同年11月30日の 資生堂(終値)のチャート。11月に $n=1$ から $n=2$ へ励起。
$n=3$ のパターンも見つかったら報告します。
おわり
記事一覧へ戻る