2020年4月21日付けのブログで、株価の変化率が、基本成長率を $r$、ゆらぎ係数を $v$、ブラウン運動を $B$ とすると、
$$\frac{dx}{dt}=rx+vx\frac{dB}{dt}\tag{1}$$
で数式化できることを示しました。式 (1) はランダムなブラウン運動項を含む確率微分方程式ですので、解はひとつに定まりません。そんな方程式が何の役に立つの?と疑問に思われるかもわかりませんが、複数の解、しかもなるべく多くの解を実際に表示することによって全体の傾向がみえます。
さて、本日は $x$ を事業体 $A$ の売上とみなします。その競争相手を $Y$ として、その売上を $y$ とします。$Y$ が $X$ に及ぼす影響の度合いを $a$、$X$ が $Y$ に及ぼす影響の度合いを $b$ とし、それぞれを競争係数 $a$、$b$ と呼び、いずれも正の値とします。
このとき、$X$ の売上 $x$, $Y$ の売上 $y$ の変化率は、式 (1) に競争項を付け加えて、それぞれ以下のように書けます。
$$\frac{dx}{dt}=r_{1}x+v_{1}x\frac{dB}{dt}-axy\tag{2}$$
$$\frac{dy}{dt}=r_{2}y+v_{2}y\frac{dB}{dt}-bxy\tag{3}$$
ここで、$a=b=0$ とすれば競争項が消えますので、$X$ と $Y$ は独立に成長します。
まずは、競争がないとき、すなわち $a=b=0$ のときの様子を確認しましょう。サンプル・パスは 50 本、縦軸は対数です。
図1
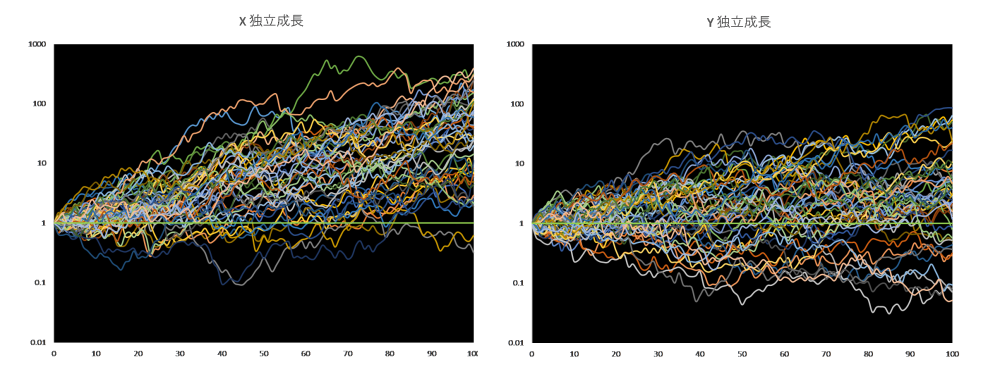
$初期値=1.0$, $r_{1}=0.05$, $r_{2}=0.03$, $v_{1}=v_{2}=0.2$, $a=b=0$ のときの計算解
サンプル・パス=50本、ブラウン運動はエクセル関数 =NORMINV(RAND(),0,1)で生成
緑の直線が「現状維持線」
初期値は $X$ も $Y$ も 1.0 です。緑の直線が 1.0 の線、つまり売上の現状維持線ですのでこれを基準にみていきます。横軸は任意の時間($t$)、縦軸が売上で、対数であることに注意してください。
突然ですが、このグラフが左から右へ流れる川だと想像してください。$t=0$ のところに七色の蛍光インクをぽつぽつと絶え間なく落とします。そうするとインクは拡散しながら右方向へ流れます。$X$ の川へ落とした蛍光インクは右上方向へ拡散していて、$Y$ の川の方はほぼ真横へ拡散しています。(この様子は移流拡散方程式によっても再現できます。ご興味のある方は、2023年1月8日付けブログ(株価の動きを数式化するひとつの方法)をご覧ください。)
これだけでもすでにかなりおもしろい結果です。事業体の売上はブラウン運動項によって絶えずランダムな刺激を受けます。その刺激の入り方によって、ある時間が経過したときの事業体の売上は初期値に対してプラス、マイナス、つまり緑線の上側と下側のいずれにも帰着します。そして、基本成長率 $r$、すなわち事業体の潜在的な成長力が大きければ大きいほど「上側」に帰着する可能性が高まります。
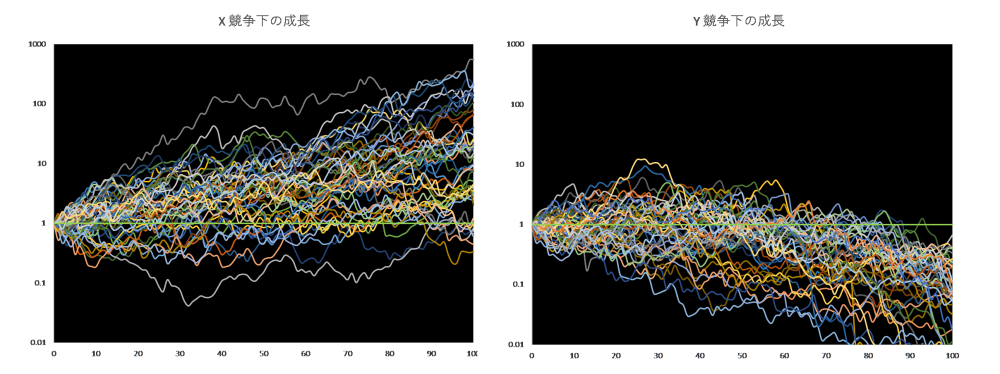
では、次に競争係数 $a$, $b$ に任意の値を入れたとき、$X$ と $Y$ の売上がどう影響を受けるかをみます。図2をご覧ください。
図2
$初期値=1.0$, $r_{1}=0.05$, $r_{2}=0.03$, $v_{1}=v_{2}=0.2$, $a=b=0.005$ のときの計算解
サンプル・パス=50本、ブラウン運動はエクセル関数 =NORMINV(RAND(),0,1)で生成
緑の直線が「現状維持線」
独立に成長するときと比較してどうでしょうか。$X$ にはあまり変化は見られませんが、$Y$ はあきらかに全体が右肩下がりになっています。これは、二社のゆらぎ係数と競争係数が同じであっても、基本成長率の違いだけで未来が大きく左右されるということを示しており、注目に値します。
では、このあたりをもう少し詳しく調べてみましょう。図4 は各シナリオにおいて、t=100 で到達した売上を小さい方から大きい方へ並べ替えたときの様子です。サンプル・パスは100本、縦軸は対数です。
図3
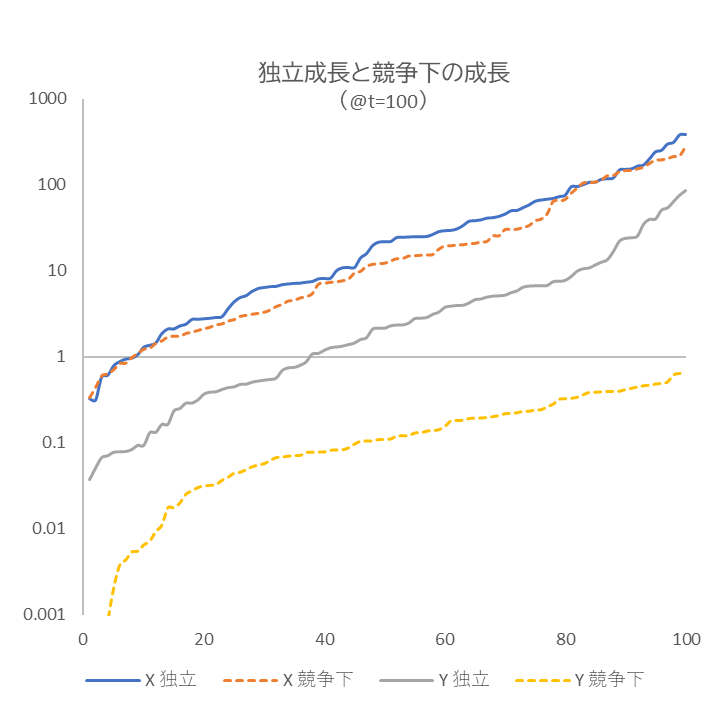
100本のサンプル・パスが t=100 で到達した売上
$初期値=1.0$, $r_{1}=0.05$, $r_{2}=0.03$, $v_{1}=v_{2}=0.2$, $a=b=0.005$
図3 から読み取れることは、
① 競争がなく $X$ と $Y$ が独立に成長する場合は $X$ の基本成長率 $r_{1}$ が $Y$ の $r_{2}$ を上回っている分、$X$ の成長(青の実線)は $Y$ の成長(グレーの実線)を絶えず上回る。
② 競争下(破線)では、上記の売上差が拡大する。青とグレーの実線間隔と、オレンジと黄の破線間隔を比較すると後者の方が明らかに大きい。つまり、基本成長率の劣る $Y$ が競争の影響をより強く受ける(競争下でも $X$ はほとんど影響を受けないが、$Y$ はすべてのパスがマイナス成長に終わっている)。
数値で確認しましょう。表1は t=100 におけるそれぞれのシナリオの平均、標準偏差、中央値です。平均は極端に大きい売上に引きずられてしまうので、中央値に注目します。中央値とはデータを小から大へ並び替えたときに中央に位置する値、つまり、図4の横軸 50 あたりの売上です。
表1
| 売上(@t=100) | X 独立成長 | Y 独立成長 | X 競争下の成長 | Y 競争下の成長 |
| 平均 | 53.4 | 8.1 | 41.1 | 0.2 |
| 標準偏差 | 81.3 | 15.8 | 62.1 | 0.2 |
| 中央値 | 22.2 | 2.2 | 12.6 | 0.1 |
式 (2), (3) において、$r_{1}=0.05$, $r_{2}=0.03$, $a=b=0.005$, $\frac{dB}{dt}$→平均0, 標準偏差1のブラウン運動
としたときの t=100 における全 100 パスの到達値の平均、標準偏差、中央値
$X$ は図1 と図2 からは違いがよくわかりませんでしたが、競争の影響を受けて中央値が 22.2 から 12.6 に下がっています。下がってはいますが初期値に対して12.6倍に成長しています。一方、$Y$ の中央値は 2.2 から 0.1 へと下がっています。競争がなければ初期値の2倍になるのに、競争したら十分の一になってしまった、ということです。
表2は 100 本のサンプル・パスが $t=100$ において、プラス・マイナスどちらの成長であるかを数えた結果です。$Y$ は独立時に63 回プラス成長しましたが、競争下では0 回でした。
表2
| X 独立 | X 競争下 | Y 独立 | Y 競争下 | |
| プラス成長 | 92 | 92 | 63 | 0 |
| マイナス成長 | 8 | 8 | 37 | 100 |
100本のサンプル・パスが t=100 でプラス成長した回数とマイナス成長した回数
$初期値=1.0$, $r_{1}=0.05$, $r_{2}=0.03$, $v_{1}=v_{2}=0.2$, $a=b=0.005$
さて、ここで図1 と 図2 をもう一度ご覧ください。毎回、このようにサンプル・パスを何本も描くのではなく、全体の特徴を示すシンプルな図が欲しいところです。キーとなる描線は、これまでの解析より、
1)現状維持を示す線(基準線)
2)中央値を示す線
3)拡散範囲を示す線
のみっつです。まとめて「三本の矢」と呼びことにします。
1)は、図1、2 の緑の直線($1.0$)です。
2)は、競争がないとき($a=b=0$) の式(2)、(3)の解析解が、それぞれ
$$x=x_{0}e^{(r_{1}-\frac{{v_{1}}^2}{2})t+v_{1}B(t)}\tag{2-1}$$
$$x=x_{0}e^{(r_{2}-\frac{{v_{2}}^2}{2})t+v_{2}B(t)}\tag{3-1}$$
であることがわかっているので、サンプル・パスは、
$$x=x_{0}e^{(r_{1}-\frac{{v_{1}}^2}{2})t}\tag{2-2}$$
$$x=x_{0}e^{(r_{2}-\frac{{v_{2}}^2}{2})t}\tag{3-2}$$
を中心にして上下に走ります。つまり、式 (2-2) と式 (3-2) が中央値線です。解析解の導出については、2023年1月23日付けのブログ(ゆらぐと成長が鈍化する不思議)をご覧ください。
3)中央値から上下にどれだけ拡散するかを示す線ですので、式 (2-2), (3-2) に $\pm{v}\sqrt{t}$を付け加えることで表現できます。(詳細は 2023年1月22日付けのブログ(ゆらぐと成長が鈍化する不思議)と、2023年2月15日付のブログ(株価の「ゆらぎを数値化する方法)を参照してください。)
$$x=x_{0}e^{(r_{1}-\frac{{v_{1}}^2}{2})t\pm{v_{1}}\sqrt{t}}\tag{2-3}$$
$$x=x_{0}e^{(r_{2}-\frac{{v_{2}}^2}{2})t\pm{v_{2}}\sqrt{t}}\tag{3-3}$$
これで準備が整ったので、早速、図1 と図 2 を「三本の矢」で表してみましょう。図4、図5 をご覧ください。緑が現状維持線、オレンジが中央値線、グレーの破線が拡散範囲です。
図4
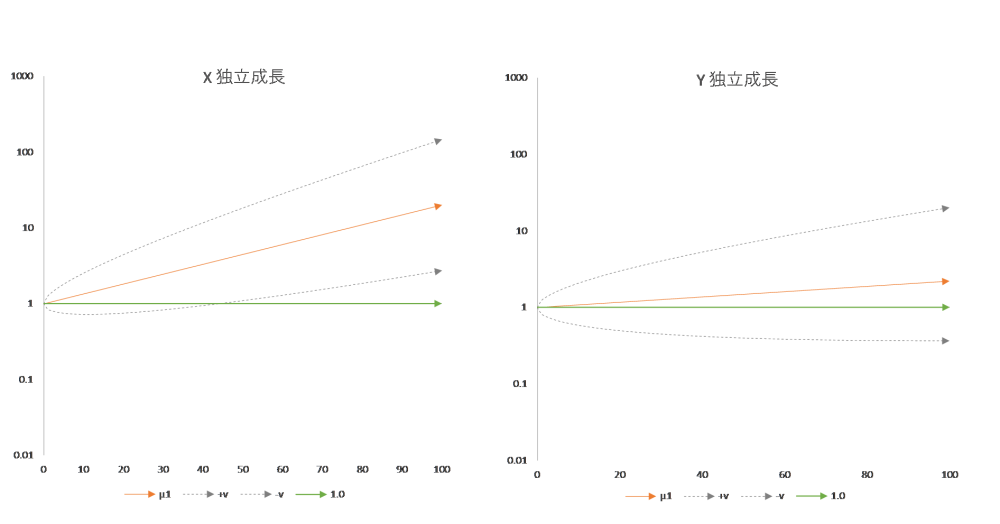
独立成長時の「三種の矢」
中央値 = $x_{100}=22.2$、 $y_{100}=2.2$
図5
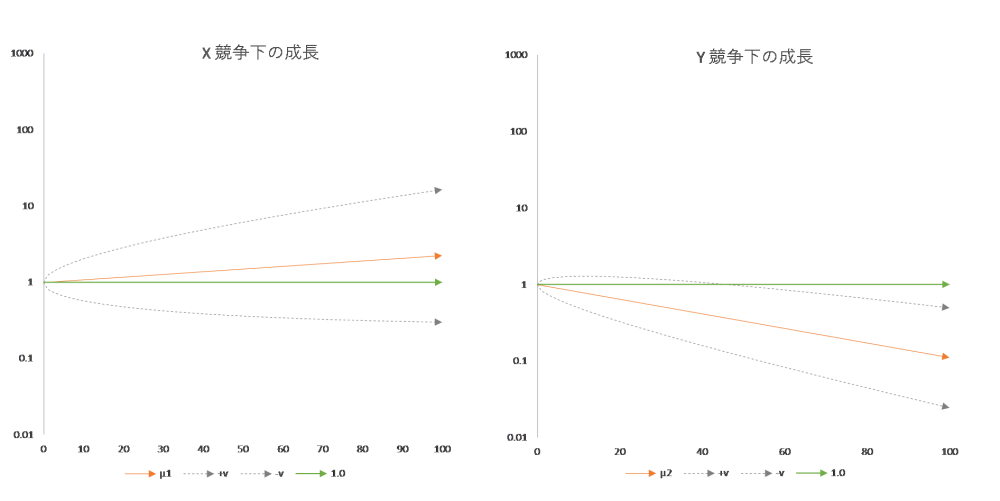
競争下の「三種の矢」
中央値 = $x_{100}=12.6$、 $y_{100}=0.1$
すっきりと特徴が表現されています。「三本の矢」が示す先、それが「未来」です。
つづく
記事一覧へ戻る